Лекция
Привет, Вы узнаете о том , что такое динамика твердого тела, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое динамика твердого тела, гироскоп, принцип работы колеса , настоятельно рекомендую прочитать все из категории Физические основы механики.
В последующих главах мы рассматриваем системы, движущиеся с нерелятивистскими скоростями. Поэтому мы снова возвращаемся к уравнениям классической нерелятивистской механики, осознавая теперь ограниченность области их применимости.
В теме 2.8 мы рассматривали кинематику твердого тела и обсуждали два типа движения: поступательное, когда все точки тела описывают одинаковые траектории, и вращательное вокруг оси, когда точки тела движутся в параллельных плоскостях и описывают окружности с центрами на оси вращения.
Любое движение твердого тела сводится к поступательному и вращательному. Произвольное движение можно представить в виде суперпозиции поступательного движения всего тела, характеризуемого движением некоторой точки (например, центра масс), и вращения тела вокруг этой точки (то есть вокруг осей, проходящих через нее).
Изучение динамики твердого тела мы начнем с простейшего случая — вращения вокруг неподвижной оси, а закончим обсуждением принципа работы колеса — гениальнейшего изобретения человечества.
Движение материальной точки характеризуется перемещением, скоростью, ускорением. Но при вращении твердого тела все его элементы имеют разные перемещения, различные скорости. Удобно найти переменные, одинаковые для всех элементов твердого тела. Мы их, собственно, уже знаем — угол поворота, угловая скорость, угловое ускорение. Соответственно, изучая динамику вращения, вместо импульса и силы мы будем оперировать их угловыми аналогами — моментом импульса и моментом силы.
Уравнение движения. В теме 4.8 было выведено уравнение движения системы материальных точек в виде
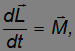
где моменты импульса и силы определялись как
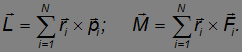
Внутренние силы между телами системы, напомним, выпали из уравнений движения. Абсолютно твердое тело можно рассматривать как систему частиц (материальных точек) с неизменными расстояниями между ними. Поэтому выписанные уравнения применимы для твердого тела, а неизменность расстояний между его точками позволяет характеризовать вращение тела вокруг неподвижной оси единственной координатой — углом поворота. Поэтому мы можем упростить приведенное выше уравнение движения. Прежде всего, нас не интересуют в данный момент напряжения, возникающие в оси. Кроме того, для описания вращения достаточно рассмотреть проекции векторов моментов импульса и силы на ось вращения.
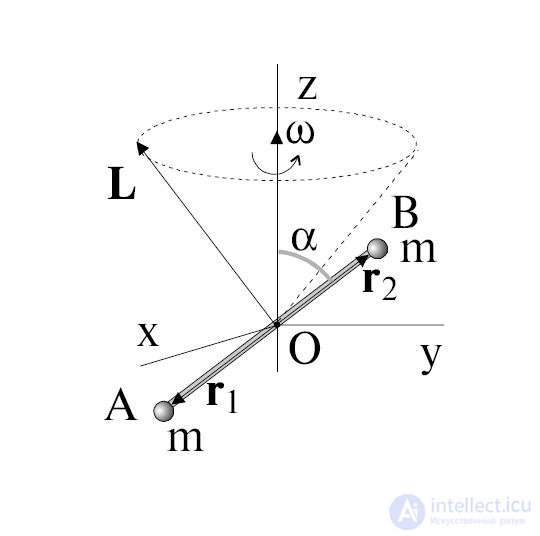
Рис. 7.1. Момент импульса L двух шаров массы m, соединенных стержнем. Вся система вращается вокруг оси z c угловой скоростью ω
Направим ось z вдоль оси вращения и выделим в твердом теле элемент массой 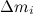 , положение которого характеризуется радиус-вектором
, положение которого характеризуется радиус-вектором 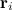 (рис. 7.2).
(рис. 7.2).
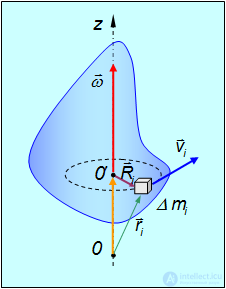
Рис. 7.2 Вращение твердого тела вокруг неподвижной оси 0z
Момент импульса этого элемента есть
Рис. 7.3. Момент импульса системы направлен вдоль оси вращения.
Радиус-вектор  можно представить как сумму его проекций на ось z и плоскость ху :
можно представить как сумму его проекций на ось z и плоскость ху :
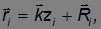
где вектор 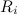 лежит в плоскости вращения и направлен от оси к выделенному элементу (см. рис. 7.1). Имеем:
лежит в плоскости вращения и направлен от оси к выделенному элементу (см. рис. 7.1). Имеем:
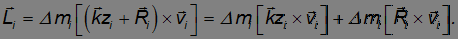
Первое слагаемое — вектор, направленный противоположно 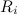 Поэтому оно не дает вклада в z-компоненту момента импульса. Второе слагаемое — вектор, направленный вдоль оси z. Так как
Поэтому оно не дает вклада в z-компоненту момента импульса. Второе слагаемое — вектор, направленный вдоль оси z. Так как
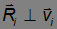
и
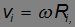
можем написать:
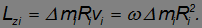
Суммируя по всем элементам тела, получаем
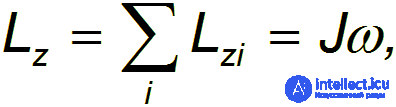
где
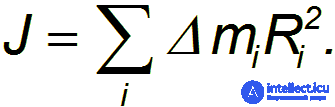
Величина 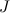 называется моментом инерции тела.
называется моментом инерции тела.
Говоря о моменте инерции, всегда указывают, относительно какой именно оси вращения он определен (в данном случае — это ось z). Момент инерции того же тела относительно какой-то другой оси примет иное значение. Сохраняется только общее правило его вычисления: берется сумма по элементам массы, составляющим тело, умноженным на квадраты расстояний этих элементов массы до оси вращения.
В случае непрерывного распределения масс с плотностью 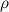 сумма заменится на интеграл по всему объему тела:
сумма заменится на интеграл по всему объему тела:
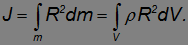
Если тело однородно, то его плотность во всех точках постоянна и 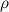 можно вынести из-под знака интеграла.
можно вынести из-под знака интеграла.
Записываем теперь уравнение движения в проекции на ось z :
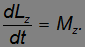
Если момент инерции не зависит от времени, то дифференцировать нужно только угловую скорость, в результате получаем основное уравнение динамики вращательного движения твердого тела в виде
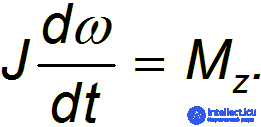
Производная угловой скорости по времени — это угловое ускорение
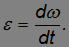
Видео 7.1. Основное уравнение динамики вращательного движения. Демонстрация, вытекающей из него связи между угловым ускорением, моментом силы и моментом инерции
Рассмотрим теперь момент внешних сил. Разложим силу 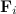 на вектор в направлении оси z и вектор, ей ортогональный:
на вектор в направлении оси z и вектор, ей ортогональный:
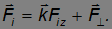
Используя снова аналогичное разложение радиус-вектора
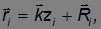
получаем для момента внешних сил 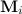 :
:
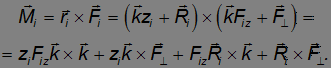
Первое слагаемое равно нулю. Два следующих содержат единичный орт — вектор k, направленный вдоль оси 0z и, следовательно, не дают вклада в проекцию 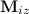 . Оба вектора
. Оба вектора
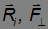
лежат в плоскости xy и, следовательно, последнее слагаемое направлено параллельно оси 0z. Если 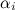 — угол между этими векторами, то
— угол между этими векторами, то
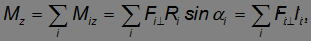
где 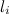 — плечо силы (см. тему. 4.8). Силу
— плечо силы (см. тему. 4.8). Силу
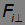
надо здесь понимать в алгебраическом смысле: она входит со знаком минус, если сила тормозит вращение.
Момент инерции. Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
Рис. 7.4. Моменты инерции различных тел
1. Момент инерции обруча относительно оси, перпендикулярной к его плоскости и проходящей через его центр.
Обруч считается бесконечно тонким, то есть толщиной обода можно пренебречь по сравнению с радиусом 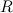 . Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения,
. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, 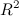 можно вынести из-под знака интеграла:
можно вынести из-под знака интеграла:
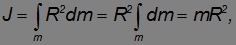
где 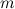 — полная масса обруча.
— полная масса обруча.
2. Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр.
Диск считается бесконечно тонким, если его толщина много меньше радиуса 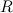 . Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусом
. Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусом  и шириной
и шириной 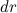 (рис. 7.5).
(рис. 7.5).
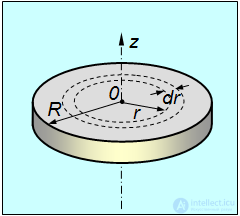
Рис. 7.5 Вычисление момента инерции диска относительно оси z, перпендикулярной его плоскости и проходящей через центр
Площадь поверхности обруча равна произведению его длины окружности на ширину: 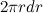 . Поскольку масса m диска распределена равномерно, масса единицы площади равна
. Поскольку масса m диска распределена равномерно, масса единицы площади равна 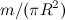 , так что масса обруча равна
, так что масса обруча равна
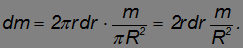
Момент инерции обруча мы уже знаем:
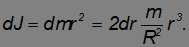
Осталось просуммировать моменты инерции всех таких обручей:
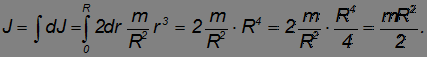
Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси.
3. Момент инерции шара относительно его диаметра.
Поступим аналогичным образом: «нарежем» шар на бесконечно тонкие диски толщиной 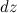 , находящиеся на расстоянии z от центра (рис. 7.6).
, находящиеся на расстоянии z от центра (рис. 7.6).
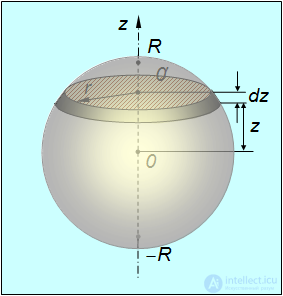
Рис. 7.6. Момент инерции шара относительно его диаметра
Радиус такого диска
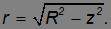
Объем диска 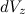 равен его площади, умноженной на толщину:
равен его площади, умноженной на толщину:
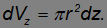
Массу диска 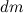 находим, разделив массу шара
находим, разделив массу шара 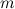 на его объем
на его объем 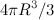 и умножив на объем диска:
и умножив на объем диска:
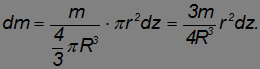
Момент инерции диска был найден выше. В применении к данному случаю он равен
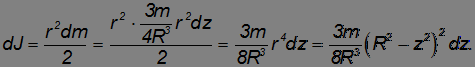
Момент инерции шара находится интегрированием по всем таким дискам:
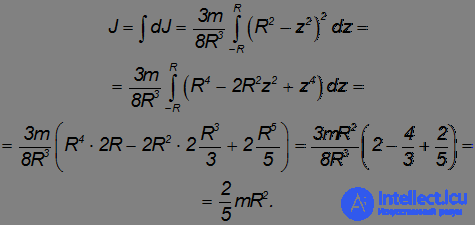
4. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню.
Пусть стержень имеет длину 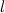 . Направим ось x вдоль стержня. Начало координат по условию находится в центре стержня (рис. 7.7).
. Направим ось x вдоль стержня. Начало координат по условию находится в центре стержня (рис. 7.7).
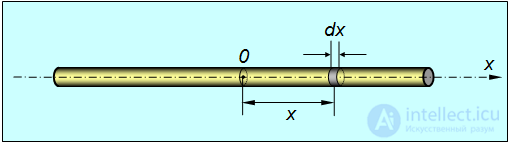
Рис. 7.7. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню
Возьмем элемент стержня длиной 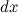 , находящийся на расстоянии x от оси вращения. Его масса равна
, находящийся на расстоянии x от оси вращения. Его масса равна
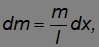
а момент инерции
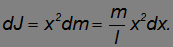
Отсюда находим момент инерции стержня:
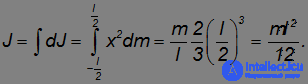
Теорема Штейнера. В приведенных примерах оси проходят через центр масс (центр инерции) тела. Момент инерции относительно других осей вращения определяется в соответствии с теоремой Штейнера:
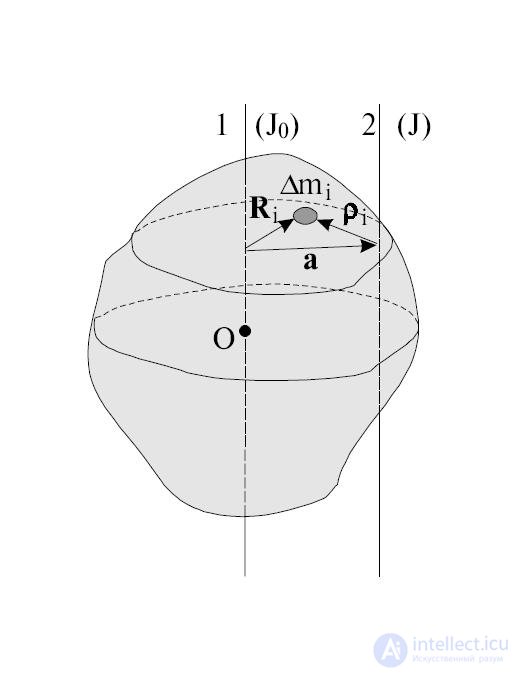
Рис. 7.8. К выводу теоремы Штейнера
Момент инерции тела относительно произвольной оси равен сумме момента инерции JC относительно параллельной оси, проходящей через центр инерции тела, и величины ma2 — произведения массы тела на квадрат расстояния от центра инерции тела до выбранной оси, то есть
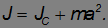
Продемонстрируем сначала применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу, возникшему при вычислении момента инерции стержня относительно оси, проходящей через его середину, но взятому в других пределах:
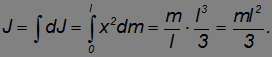
Расстояние до оси, проходящей через центр масс, равно a = l/2. По теореме Штейнера получаем тот же результат:
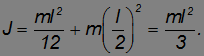
Вывод теоремы Штейнера иллюстрируется рис. 7.8, 7.9
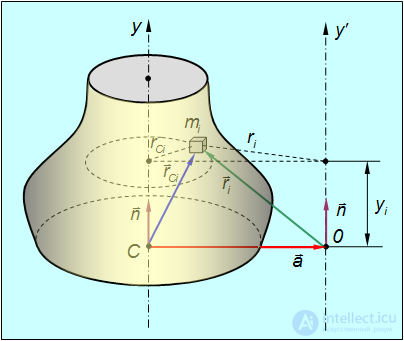
Рис. 7.9. К выводу теоремы Штейнера
Пусть одна ось проходит в направлении единичного вектора n через центр масс С твердого тела (системы тел), а другая — параллельно ей через некоторую точку 0. Из центра масс в направлении второй оси проводим ортогональный осям вектор a, который определяет положение точки 0. Радиус-векторы некоторого элемента системы массой 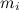 относительно точек С и 0 обозначаем
относительно точек С и 0 обозначаем 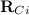 и
и 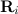 , соответственно. Момент инерции этого элемента относительно оси С есть
, соответственно. Момент инерции этого элемента относительно оси С есть
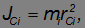
где 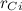 — расстояние элемента от оси. По теореме Пифагора (см. рис. 7.9).
— расстояние элемента от оси. По теореме Пифагора (см. рис. 7.9).
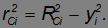
Катет 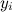 равен проекции векторов
равен проекции векторов 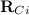 и
и 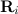 на ось вращения, то есть
на ось вращения, то есть
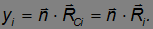
Используя эти выражения и суммируя по всем элементам системы, находим момент инерции относительно оси, проходящей через точку С, и, аналогичным образом, момент инерции относительно параллельной оси, проходящей через точку 0 :
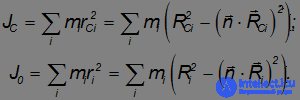
Здесь выражение для 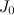 получено из
получено из 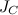 простой заменой
простой заменой 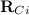 на
на 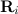 .
.
Как видно из рис. 7.9, векторы 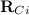 и
и 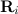 связаны между собой:
связаны между собой:
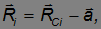
причем
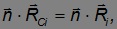
так как векторы n и а ортогональны и их скалярное произведение
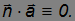
Тогда мы можем преобразовать выражение для 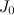 :
:
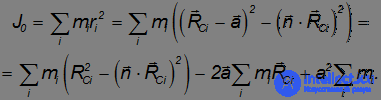
Первое слагаемое в правой части — момент инерции 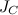 относительно оси, проходящей через точку C. Третье слагаемое равно
относительно оси, проходящей через точку C. Третье слагаемое равно 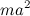 , где
, где
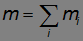
— полная масса системы.
Второе слагаемое равно нулю, так как оно пропорционально радиус-вектору центра инерции относительно самого центра инерции. Окончательно:
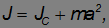
что и требовалось доказать.
Теорема Штейнера связывает моменты инерции относительно параллельных осей. Иногда оказывается полезной другая теорема, связывающая моменты инерции относительно трех взаимно перпендикулярных осей. Однако эта теорема относится только к плоским фигурам, толщиной которых можно пренебречь по сравнению с размерами в двух других направлениях. Итак, теорема о моментах инерции плоских фигур:
Если через произвольную точку 0 плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, лежащих в плоскости фигуры и проходящих через эту же точку 0.
Иными словами, берем на фигуре произвольную точку 0 и проводим координатные оси так, чтобы 0x и 0y лежали в плоскости фигуры. Тогда, согласно теореме, момент инерции относительно оси 0z равен сумме моментов инерции относительно осей 0x и 0y:
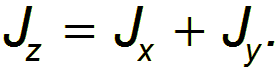
При этом расположение осей 0x, 0y может быть произвольным; главное, чтобы они лежали в плоскости фигуры (рис. 7.10).
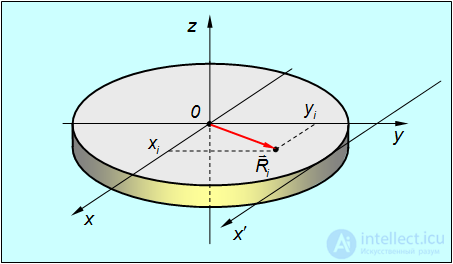
Рис. 7.10. Моменты инерции плоской фигуры относительно взаимно перпендикулярных осей
Из рисунка видно, что
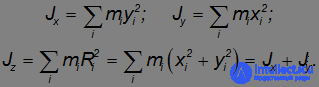
что и требовалось доказать.
Найдем, например, момент инерции 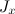 диска относительно его диаметра. Два ортогональных диаметра диска равноправны, поэтому
диска относительно его диаметра. Два ортогональных диаметра диска равноправны, поэтому
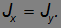
Согласно теореме о плоской фигуре
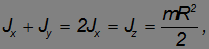
откуда
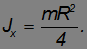
Теперь можно применить теорему Штейнера, чтобы найти, например, момент инерции 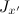 относительно оси
относительно оси 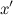 , параллельной диаметру и проходящей через край диска (см. рис. 7.10):
, параллельной диаметру и проходящей через край диска (см. рис. 7.10):
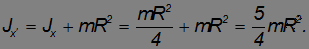
Определим работу, которую совершают внешние силы при вращении твердого тела вокруг неподвижной оси 00. Элементарная работа по перемещению элемента массой 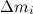 равна:
равна:
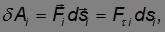
где 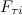 — тангенциальная составляющая внешней силы
— тангенциальная составляющая внешней силы 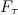 , действующей на элемент массой
, действующей на элемент массой 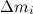 (рис. 7.11).
(рис. 7.11).
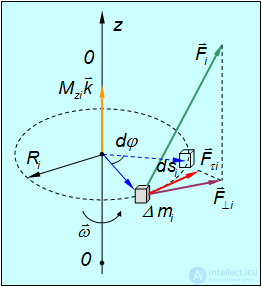
Рис. 7.11. Работа сил при вращении твердого тела
Вспомним разложение силы
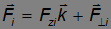
на вектор, параллельный оси вращения (примем ее за ось z), и вектор, ортогональный к ней. При вращении перемещение направлено по касательной к траектории, то есть, во-первых, лежит в плоскости вращения. Отсюда следует, что сила 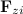 , направленная вдоль оси вращения, работы не совершает. Во-вторых, перемещение ортогонально радиусу окружности, описываемой данным элементом. Проекцию внешней силы на плоскость вращения в свою очередь можно разложить на слагаемые
, направленная вдоль оси вращения, работы не совершает. Во-вторых, перемещение ортогонально радиусу окружности, описываемой данным элементом. Проекцию внешней силы на плоскость вращения в свою очередь можно разложить на слагаемые
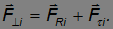
Одно из них (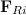 ) направлено по радиусу, оно ортогонально перемещению и потому также не совершает работы. Работу совершает лишь проекция силы на касательное направление
) направлено по радиусу, оно ортогонально перемещению и потому также не совершает работы. Работу совершает лишь проекция силы на касательное направление 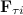 , фигурирующая в выражении для элементарной работы.
, фигурирующая в выражении для элементарной работы.
Путь 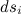 можно записать как
можно записать как
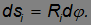
Таким образом,
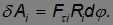
Заметим, что
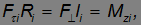
где 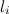 — введенное выше плечо силы.
— введенное выше плечо силы.
Следовательно, мы выразили элементарную работу при перемещении элемента массой 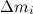 через проекцию момента внешней силы на ось вращения:
через проекцию момента внешней силы на ось вращения:
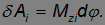
Поэтому элементарная работа при вращении всего твердого тела равна
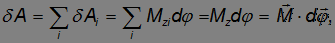
где M есть полный момент всех внешних сил, а вектор 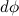 направлен вдоль оси вращения согласно правилу буравчика.
направлен вдоль оси вращения согласно правилу буравчика.
Для полной работы за время 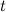 можно записать:
можно записать:
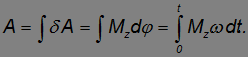
Проекцию момента внешних сил можно выразить через угловое ускорение, используя основное уравнение динамики вращательного движения
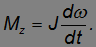
Тогда, с учетом 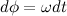 , получаем
, получаем
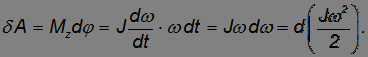
Согласно закону сохранения энергии работа 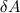 равняется приращению
равняется приращению 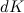 кинетической энергии твердого тела. Об этом говорит сайт https://intellect.icu . Таким образом, кинетическая энергия вращающегося тела равна
кинетической энергии твердого тела. Об этом говорит сайт https://intellect.icu . Таким образом, кинетическая энергия вращающегося тела равна
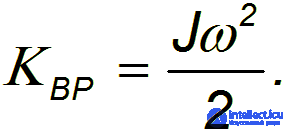
Между величинами, описывающими поступательное и вращательное движения, существует аналогия, которая облегчает усвоение и запоминание этих величин и связей между ними (см. таблицу).
Таблица
Аналогия между поступательным и вращательным движениями
| Поступательное движение | Вращательное движение |
|---|---|
Перемещение 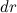 |
Поворот 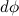 |
Скорость 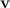 |
Угловая скорость 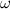 |
Ускорение 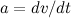 |
Угловое ускорение 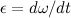 |
Масса 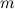 |
Момент инерции 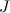 |
Импульс 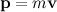 |
Момент импульса 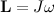 |
Сила 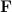 |
Момент силы 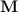 |
Уравнение движения 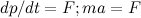 |
Уравнение движения 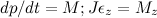 |
Работа 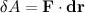 |
Работа 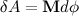 |
Кинетическая энергия 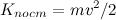 |
Кинетическая энергия
|
Рассмотрим теперь плоское движение твердого тела, то есть движение, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Пример такого движения — вращение колеса автомобиля при его движении по прямой. Можно взять любую точку 0 тела и мысленно провести через нее ось вращения перпендикулярно плоскостям, в которых лежат траектории точек тела. Тогда ось вращения будет двигаться поступательно, оставаясь все время параллельной самой себе.
Видео 7.2. Плоское движение твердого тела в однородном поле тяжести. Полет плоской картонной фигуры
Соответственно, скорость 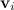 элементарной массы
элементарной массы 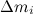 твердого тела складывается из скорости
твердого тела складывается из скорости 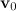 поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:
поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:
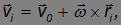
где 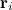 — радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.
— радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.
Кинетическая энергия элементарной массы равна тогда:
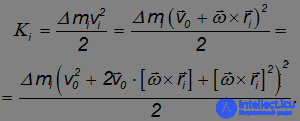
Векторное произведение
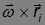
имеет модуль, равный 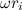 , где
, где 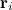 — расстояние массы
— расстояние массы 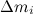 от оси вращения. Следовательно, третье слагаемое в скобках равно
от оси вращения. Следовательно, третье слагаемое в скобках равно 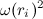 . Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:
. Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:
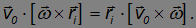
В результате получим для кинетической энергии элемента твердого тела следующее выражение
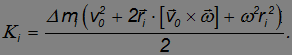
Для нахождения кинетической энергии тела просуммируем по всем элементарным массам:
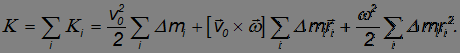
Сумма элементарных масс
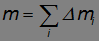
есть масса твердого тела. Выражение
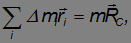
где 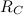 — радиус-вектор центра масс тела относительно точки 0.
— радиус-вектор центра масс тела относительно точки 0.
Наконец,
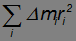
— есть момент инерции тела 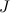 относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:
относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:
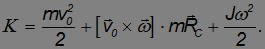
Поскольку выбор мысленной оси вращения всецело в нашей власти, мы упростим полученное выражение, взяв в качестве точки 0 центр масс тела. Тогда 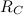 = 0 и кинетическая энергия тела при плоском движении равна
= 0 и кинетическая энергия тела при плоском движении равна
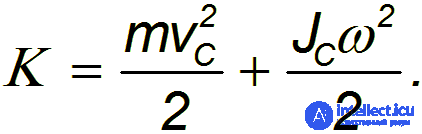
Здесь 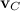 — скорость движения центра масс, a
— скорость движения центра масс, a 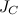 — момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.
— момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.
Движение твердого тела определяется действующими на тело внешними силами и моментами этих сил
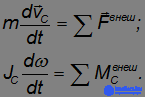
Индекс 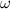 в обозначениях для момента внешней силы означает проекцию момента на ось вращения.
в обозначениях для момента внешней силы означает проекцию момента на ось вращения.
В следующих примерах мы имеем дело с плоским движением.
Видео 7.3. Зависимость поведения цилиндров на наклонной плоскости от характера распределение массы по их объему
Пример 1. Круглое однородное тело (обруч, цилиндр, шар) радиусом 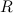 и массой
и массой 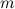 скатывается без скольжения по наклонной плоскости под углом
скатывается без скольжения по наклонной плоскости под углом 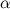 к горизонту с высоты
к горизонту с высоты 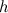 (рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.
(рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.
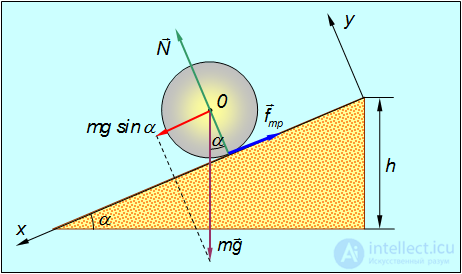
Рис. 7.12. Скатывание тела с наклонной плоскости
Рассмотрение данной задачи можно вести двумя способами.
1-й способ. По условию тело катится без проскальзывания. Это условие используется у нас дважды. Сила трения между телом и плоскостью действует в точке соприкосновения и в отсутствие скольжения не превышает своего максимального значения:

где 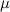 — коэффициент трения скольжения.
— коэффициент трения скольжения.
Оси координат удобно направить следующим образом: ось х — вдоль движения, ось у — перпендикулярно наклонной плоскости. Тело движется под действием трех сил: силы тяжести 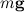 , силы трения
, силы трения 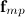 и силы нормального давления
и силы нормального давления 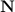 , так что уравнение поступательного движения центра инерции тела имеет вид:
, так что уравнение поступательного движения центра инерции тела имеет вид:
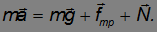
Вдоль оси у тело не движется. Проецируя уравнение движения центра масс на ось у, получаем для силы нормального давления соотношение:

Проекция уравнения движения на ось х дает:

Так как линейная скорость точек соприкосновения цилиндра с наклонной плоскостью равна нулю (опять используем условие отсутствия проскальзывания), то скорость (ускорение) поступательного движения связаны с угловой скоростью (угловым ускорением) тела обычными соотношениями:

Кроме поступательного движения, тело еще и вращается. Вращение удобно описывать относительно оси z, проходящей через центр масс цилиндра.
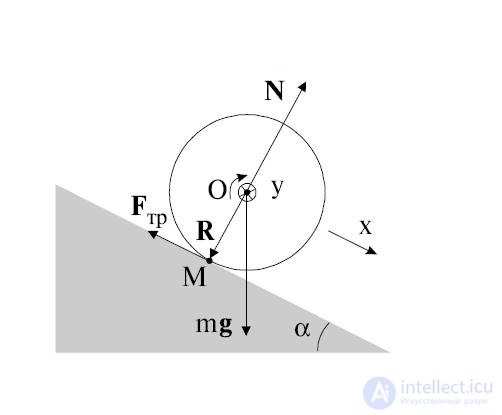
Выбор этот обусловлен тем, что линии действия силы тяжести и силы нормального давления плоскости проходят через ось вращения и, следовательно, моменты этих сил равны нулю. Таким образом, цилиндр вращается только под действием силы трения, и уравнение вращательного движения имеет вид:
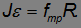
Таким образом, получается система 4-х уравнений, описывающих поступательное и вращательное движение с дополнительным неравенством, выражающим закон трения. Решая систему уравнений, находим:
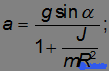
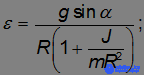

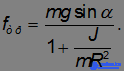
Чем больше момент инерции относительно оси, проходящей через центр масс, тем меньше ускорение тела. Мы уже получили ответ на один из вопросов задачи: шар будет двигаться быстрее цилиндра, а цилиндр — быстрее обруча. Подставляя решение для силы трения в неравенство, выражающее закон трения, находим условие, при котором будет отсутствовать проскальзывание:
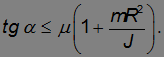
Смысл этого условия прост: наклон не должен быть слишком крут.
Итак, центр масс тела движется вдоль плоскости с постоянным ускорением a, так что зависимость пройденного пути и скорости от времени имеет вид:
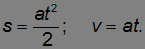
Отсюда следует связь скорости и пройденного пути:
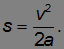
К концу спуска тело проходит путь
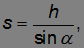
так что его скорость достигает величины
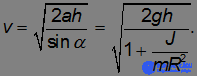
Подставляя сюда моменты инерции обруча (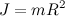 ), цилиндра (
), цилиндра (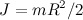 ) и шара (
) и шара (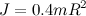 ), находим соответственно:
), находим соответственно:
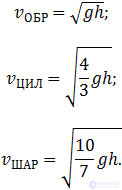
2-й способ. Используем закон сохранения полной энергии. В конце спуска тело приобретает кинетическую энергию
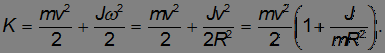
Эта кинетическая энергия приобретена за счет потенциальной энергии 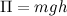 . Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.
. Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.
В рассмотренном выше примере мы считали примере мы имели дело со случаем, когда проскальзывание отсутствовало. Это позволило утверждать простую связь (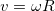 ) между угловой и линейной скоростями тела и его радиусом. Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.
) между угловой и линейной скоростями тела и его радиусом. Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.
Силы трения, как уже говорилось, направлены так, чтобы препятствовать относительному проскальзыванию соприкасающихся тел. Часто путают это возможное проскальзывание с осуществляемым поступательным движением. Необходимо четко понимать, что не редки случаи, когда сила трения не тормозит, но ускоряет тело, то есть направлена по его движению. Самый известный пример — трогание автомобиля с места. Колеса начинают вращаться и проскальзывают по земле назад. Соответственно, сила трения направлена вперед, и именно она заставляет автомобиль трогаться. Чтобы ближе познакомиться с подобными случаями, рассмотрим пример.
Пример 2. Цирковой артист бросает на арену обруч массой 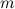 и радиусом
и радиусом 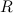 , который начинает катиться в горизонтальном направлении со скоростью
, который начинает катиться в горизонтальном направлении со скоростью 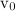 (рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью
(рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью 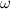 . Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость
. Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость 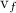 поступательного движения обруча.
поступательного движения обруча.
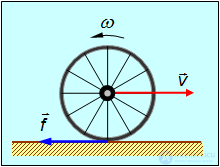
Рис. 7.13. Движение обруча с обратным вращением
При обратном вращении обруча точка его касания с ареной движется вперед как из-за вращения, так и из-за поступательного движения обруча. Поэтому неизбежно существует проскальзывание и, значит, сила трения достигает своего максимального значения. Она тормозит как поступательное движение, так и вращение обруча. Может случиться так, что поступательное движение обруча будет остановлено в тот момент, когда он еще сохраняет обратное вращение. Далее сила трения начнет ускорять обруч по направлению к артисту. Ускорение это прекратится, когда исчезнет тенденция к проскальзыванию, после чего обруч покатится назад равномерно с некоторой установившейся скоростью 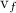 . Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.
. Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.
Направим ось ОХ направо (в направлении красной стрелки на рис. 7.13), ось вращения ОZ направим на нас (см. следующий пример, там эту ось удобнее направить от нас, то есть за чертеж), то есть в направлении «обратного» вращения, ось OY направим как обычно, вверх. Плоское движение обруча представим как суперпозицию его поступательного движения вместе с центром масс (геометрическим центром, поскольку обруч предполагается однородным). Спроектируем линейные и угловые скорости на соответствующие оси. Тогда, до тех пор, пока сила трения есть сила трения скольжения и направлена она налево, уравнения движения имеют вид
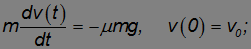
(7.3.1)
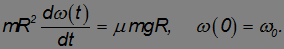
(7.3.2)
Уравнение (7.3.1) описывает движение центра масс обруча, а уравнение (7.3.2) его вращение вокруг оси проходящей через центр масс в той системе отсчета, в которой она покоится (системе центра масс). В (7.3.2) учтено, что момент инерции однородного обруча относительно его оси симметрии равен 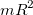 . После элементарного интегрирования получаем
. После элементарного интегрирования получаем
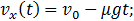
(7.3.3)
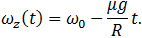
(7.3.4)
Поступательное движение прекратится, то есть 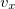 станет равным нулю, в момент времени
станет равным нулю, в момент времени
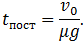
(7.3.5)
Вращение прекратится, то есть 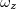 станет равным нулю,в момент времени
станет равным нулю,в момент времени
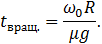
(7.3.6)
Их отношение
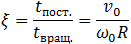
(7.3.7)
может быть любым ввиду независимости начальных скоростей поступательного 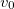 и вращательного
и вращательного 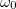 движений.
движений.
Для дальнейшего анализа введем в рассмотрение скорость 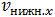 нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем
нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем
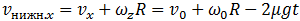
(7.3.8)
Если 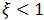 , то первым прекратится поступательное движение обруча. В момент времени
, то первым прекратится поступательное движение обруча. В момент времени 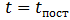 скорости (7.3.3) и (7.3.8) будут иметь значения
скорости (7.3.3) и (7.3.8) будут иметь значения
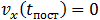
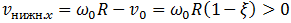
Нижняя точка обруча, за счет продолжающегося вращения, будет по-прежнему скользить относительно арены направо (направо на рисунке 7.13), сила трения скольжения сохранит свою величину и направление налево. Соответственно, центр обруча начнет ускорятся налево, то есть 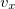 станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при
станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при 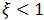 обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.
обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.
Как следует из (7.3.8), в момент времени
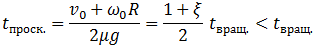
(7.3.9)
скорость нижней точки обруча 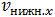 из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс
из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс
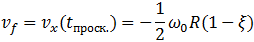
(7.3.10)
вращаясь против часовой стрелки с постоянной угловой скоростью
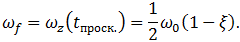
(7.3.11)
Если 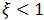 , то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени
, то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени 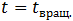 скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:
скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:
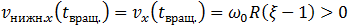
(7.3.12)
Скольжение остается, сила трения скольжения сохраняет свою величину и направление налево, но обруч под действием этой силы трения скольжения начинает вращаться по часовой стрелке (напоминаем: налево, направо, по или против часовой стрелки — на рисунке 10). В результате этого скорость центра масс (центра обруча) будет уменьшаться, скорость вращения увеличиваться, в момент времени
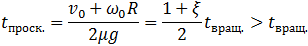
(7.3.13)
проскальзывание обруча прекратится и обруч начнет равномерно удаляться от артиста со скоростью центра (7.3.10) и угловой скоростью вращения (7.3.11). Напомним, что в этом случае  , так что
, так что 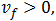 а
а 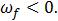
Таким образом, ответ на вопрос: "Вернется обруч или укатится?" определяется начальными условиями, а конкретнее величиной параметра 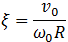 , который имеет простой физический смысл: это отношение модуля
, который имеет простой физический смысл: это отношение модуля
скорости любой точки обруча за счет его поступательного движения вместе с центром масс к модулю скорости той же точки за счет вращения обруча вокруг оси, проходящей через его центр масс, в начальный момент времени.
Пример 3. Описать движение обруча (см. предыдущий пример), если ему придано прямое вращение (рис. 7.14). Поскольку обруч вращается теперь на рис. 7.14 по часовой стрелке, направим ось вращения OZ от нас, то есть за чертеж — в отличие от предыдущего случая.
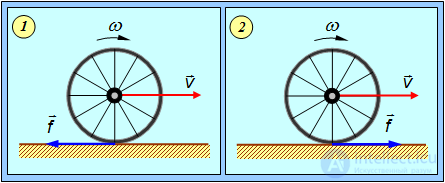
Рис. 7.14. Движение обруча с прямым вращением: 1 – 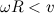 ; 2 –
; 2 – 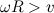
Начальная скорость нижней точки обруча складывается из скорости поступательного движения 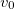 и линейной скорости
и линейной скорости 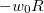 за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.
за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.
1 случай  или
или 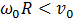 . Тогда начальная скорость
. Тогда начальная скорость 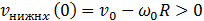 нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость
нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость 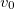 . Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид
. Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид
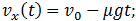
(7.3.14)
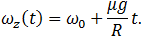
(7.3.15)
При новом выборе направления оси вращения скорость нижней точки обруча записывается в виде
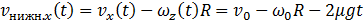
(7.3.16)
Момент 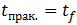 исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:
исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:
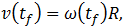
откуда находим:
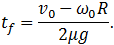
Скорость поступательного движения обруча в этот момент становится равной
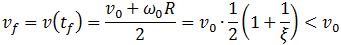
и остается потом неизменной. Эта скорость меньше начальной скорости поступательного движения обруча.
2 случай 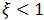 или
или 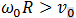 . В этом случае скорость нижней точки обода отрицательна, направлена против скорости
. В этом случае скорость нижней точки обода отрицательна, направлена против скорости 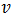 . Значит, сила трения
. Значит, сила трения 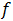 направлена по
направлена по 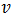 (см. рис.11-2).
(см. рис.11-2).
Соответственно, в уравнениях движения и их решениях (7.3.14) и (7.3.15) надо изменить знаки на противоположные перед вторыми слагаемыми, содержащими изменившую направление силу трения, получаем:
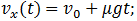
(7.3.17)
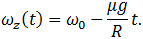
(7.3.18)
Соответственно, выражение для скорости нижней точки обруча приобретает вид:
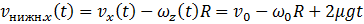
(7.3.19)
Момент прекращения проскальзывания 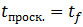 определяется аналогично и оказывается равным:
определяется аналогично и оказывается равным:
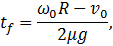
а для скорости установившегося движения получается вновь выражение
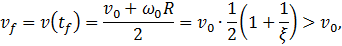
но в данном случае она будет больше (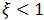 ) начальной скорости поступательного движения.
) начальной скорости поступательного движения.
Объединяя оба случая в один, записываем окончательный результат:
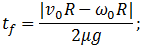
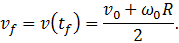
Если какое-либо тело привести во вращение относительно произвольной оси и затем предоставить самому себе, то положение оси вращения в пространстве, вообще говоря, изменится: ось будет либо поворачиваться, либо перемещаться относительно инерциальной системы отсчета. Для того, чтобы произвольно взятую ось удерживать в неизменном положении, к ней необходимо приложить определенные силы.
Ось вращения тела, положение которой в пространстве сохраняется без приложения извне каких-либо сил, называется свободной осью тела.
Можно показать, что существуют по крайне мере три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями. Такие оси называются главными осями инерции тела.
Моменты инерции тела относительно главных осей называются главными моментами инерции.
Для тел, обладающих осевой симметрией (например, у однородного цилиндра), одна из главных осей совпадает с осью симметрии, а две любые оси, перпендикулярные к оси симметрии и друг другу и проходящие через центр масс тела, также являются главными (рис. 7.15). Моменты инерции относительно двух последних осей равны друг другу, а момент инерции относительно оси симметрии отличен от них
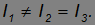
Такое тело называется симметричным волчком.
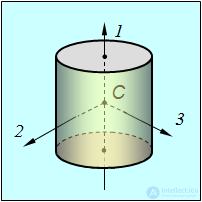
Рис. 7.15. Главные оси однородного цилиндра
У тела с центральной симметрией (например, у однородного шара) любые три взаимно перпендикулярные оси, проходящие через центр симметрии, являются главными. Для них
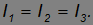
Такие тела называются шаровыми волчками. Любая ось шарового волчка, проходящая через центр симметрии, является главной (а, значит, и свободной).
В общем случае главные моменты инерции тела различны, то есть
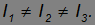
Такое тело называется асимметричным волчком. Примером асимметричного волчка может служить однородный прямоугольный параллелепипед (рис. 7.16).
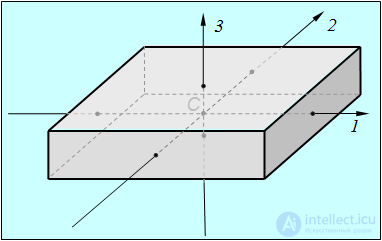
Рис. 7.16. Главные оси однородного параллелепипеда
При «почти» свободном вращении на тело могут действовать малые возмущения. Если при таких возмущениях ось вращения мало изменяет свое положение, то вращение называется устойчивым. В противном случае говорят о неустойчивом вращении.
Пусть для асимметричного волчка для определенности имеет место следующее соотношение между главными моментами инерции:
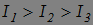
Можно показать, что вращение вокруг осей 1 и 3 (то есть осей с максимальными и минимальными моментами инерции) будет устойчивым, а вокруг оси 2 (с промежуточным по величине моментом инерции) — неустойчивым.
Видео 7.4. Устойчивость полета в воздухе прямоугольного параллелепипеда
Пусть тело вращается вокруг одной из главных осей, например, вокруг оси z. Тогда вектор угловой скорости имеет вид
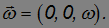
Компоненты момента импульса тела будут равны
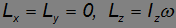
или в векторном виде
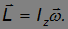
То есть этом случае момент импульса параллелен оси вращения
Видео 7.5. Устойчивое вращение стержня, диска и цепочки вокруг той свободной оси, которой соответствует максимальный момент инерции
Если тело вращается в отсутствие внешних сил (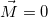 ), то согласно закону сохранения момента импульса в этом случае
), то согласно закону сохранения момента импульса в этом случае
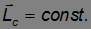
В общем случае вектор угловой скорости вращается вокруг момента импульса. Однако если ось вращения совпадает с одной из главных осей, то ось вращения сохраняет свою ориентацию в пространстве в отсутствие внешних сил.
Гироскопом называется массивное осесимметричное тело (симметричный волчок), быстро вращающееся вокруг оси симметрии, причем ось вращения может изменять положение в пространстве. Ось симметрии называется осью фигуры гироскопа.
Видео 7.6. Что же такое гироскоп?

Рис. 7.17. Движение системы гироскопов
Ось симметрии является одной из главных осей гироскопа. Поэтому его момент импульса совпадает по направлению с осью вращения.
Для того, чтобы изменить положение в пространстве положение оси фигуры гироскопа, необходимо подействовать на него моментом внешних сил.
Видео 7.7. Гироскопические силы:большой гироскоп рвет веревку
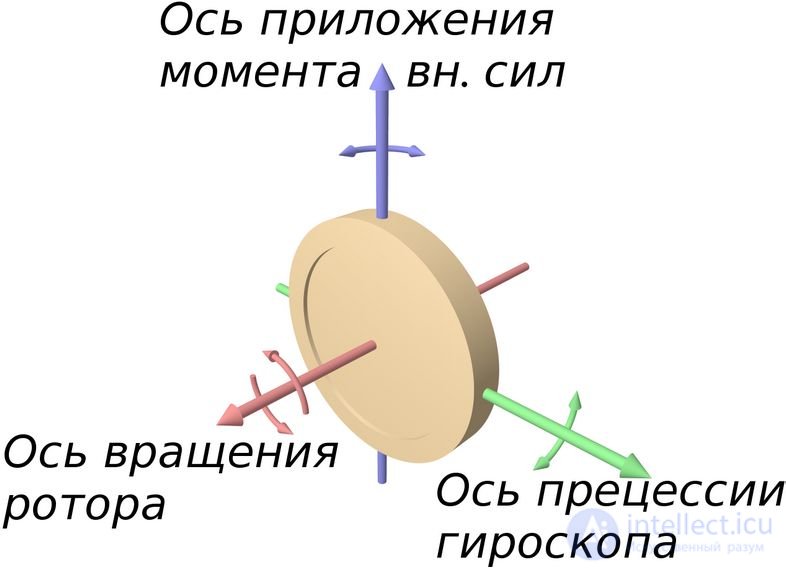
Рис. 7.18. Направление векторов при вращении гироскопа
При этом наблюдается явление, получившее название гироскопического: под действием сил, которые, казалось бы, должны были вызвать поворот оси 1 вокруг оси 2 (рис. 7.19), наблюдается поворот оси фигуры вокруг оси 3.
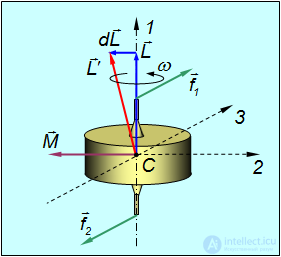
Рис. 7.19. Движение оси фигуры гироскопа под действием момента внешних сил
Видео 7.8. Гироскоп с перегрузами: направление и скорость прецессии, нутации
Гироскопические явления проявляются всюду, где имеются быстро вращающиеся тела, ось которых может поворачиваться в пространстве.
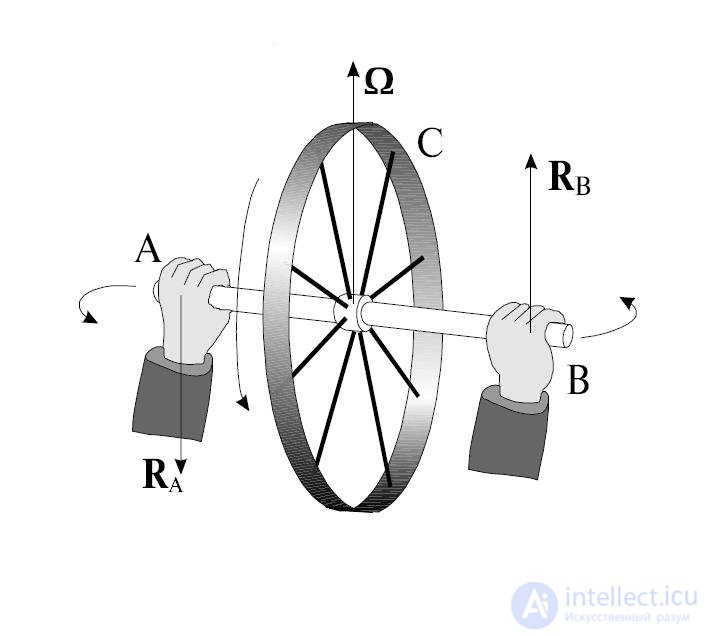
Рис. 7.20. Реакция гироскопа на внешнее воздействие
Странное на первый взгляд поведение гироскопа, рис. 7.19 и 7.20, полностью объясняется уравнением динамики вращательного движения твердого тела
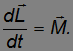
Видео 7.9. «Любвеобильный» гироскоп: ось гироскопа бежит вдоль направляющей, не покидая ее
Видео 7.10. Действие момента силы трения: «Колумбово» яйцо
Если гироскоп привести в быстрое вращение, он будет обладать значительным моментом импульса. Если на гироскоп будет действовать внешняя сила в течение времени 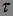 , то приращение момента импульса будет
, то приращение момента импульса будет
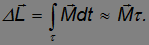
Если сила действует в течение короткого времени 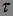 , то
, то
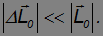
Другими словами, при коротких воздействиях (толчках) момент импульса гироскопа практически не меняется. С этим связана замечательная устойчивость гироскопа по отношению к внешним воздействиям, которая используется в различных приборах, таких как гирокомпасы, гиростабилизированные платформы и т. д.
Видео 7.11. Модель гирокомпаса, гиростабилизация
Видео 7.12. Большой гирокомпас

7.21. Гиростабилизатор орбитальной станции
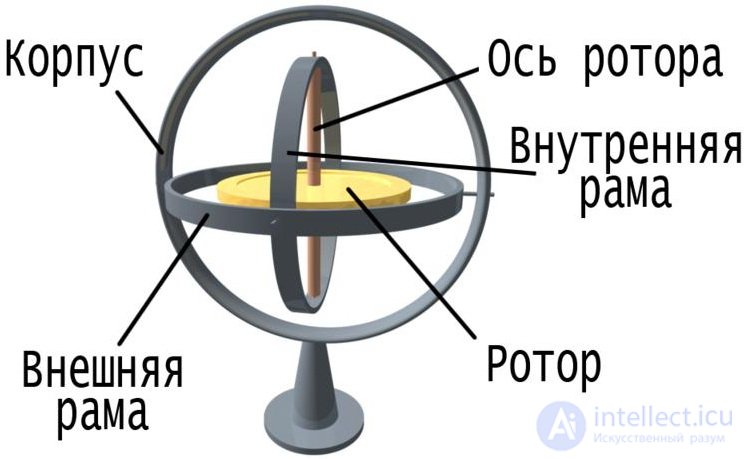
В гироскопах, применяющихся в авиации и космонавтике, используется карданов подвес, который позволяет сохранять направление оси вращения гироскопа независимо от ориентации самого подвеса:
Видео 7.13. Гироскопы в цирке: езда на одном колесе по проволоке
Рассмотрим движение гироскопа с неподвижной точкой опоры, как показано на на рис. 7.22.
Движение гироскопа под действием внешней силы называется вынужденной прецессией.
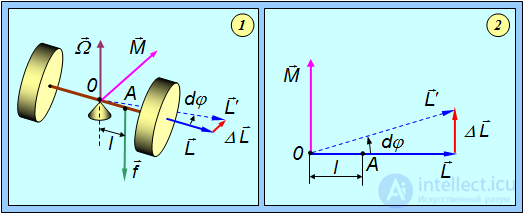
Рис. 7.22. Вынужденная прецессия гироскопа: 1 — общий вид; 2 — вид сверху
Приложим в точке А силу 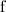 . Если гироскоп не вращается, то, естественно, правый маховик будет опускаться, а левый — подниматься. Другая ситуация будет, если предварительно гироскоп привести в быстрое вращение. В этом случае под действием силы
. Если гироскоп не вращается, то, естественно, правый маховик будет опускаться, а левый — подниматься. Другая ситуация будет, если предварительно гироскоп привести в быстрое вращение. В этом случае под действием силы 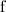 ось гироскопа будет вращаться с угловой скоростью
ось гироскопа будет вращаться с угловой скоростью 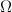 вокруг вертикальной оси. То есть ось гироскопа приобретает скорость в направлении, перпендикулярном направлению действующей силы.
вокруг вертикальной оси. То есть ось гироскопа приобретает скорость в направлении, перпендикулярном направлению действующей силы.
Таким образом, прецессия гироскопа представляет собой движение под действием внешних сил, происходящее таким образом, что ось фигуры описывает коническую поверхность.
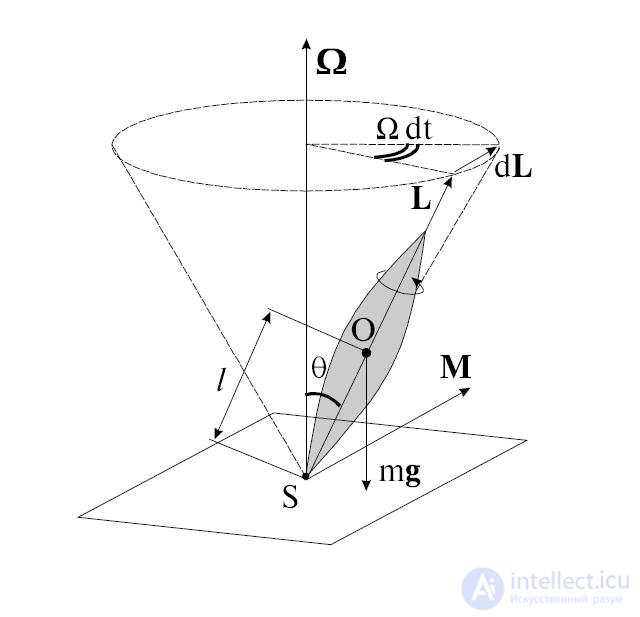
Рис. 7.23. К выводу формулы прецессии гироскопа.
Объяснение этого явления заключается в следующем. Момент силы 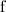 относительно точки 0 будет
относительно точки 0 будет
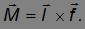
Приращение момента импульса гироскопа за время 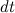 равно
равно
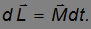
Это приращение перпендикулярно моменту импульса и, следовательно, меняет его направление, но не величину.
Вектор момента импульса ведет себя подобно вектору скорости при движении частицы по окружности. В последнем случае приращения скорости 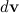 перпендикулярно скорости частицы
перпендикулярно скорости частицы 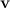 и равно по модулю
и равно по модулю
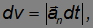
где
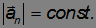
В случае гироскопа элементарное приращение момента импульса
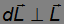
и равно по модулю
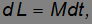
причем
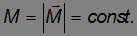
За время 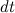 вектор момента импульса повернется на угол
вектор момента импульса повернется на угол 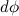
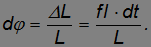
Угловая скорость вращения плоскости, проходящей через ось конуса, описываемого осью фигуры, и ось фигуры, называется угловой скоростью прецессии гироскопа.
Возникающие при определенных условиях колебания оси фигуры гироскопа в плоскости, проходящей через ось указанного выше конуса и саму ось фигуры, называются нутациями. Нутации могут быть вызваны, например, коротким толчком оси фигуры гироскопа вверх или вниз (см. рис. 7.24):
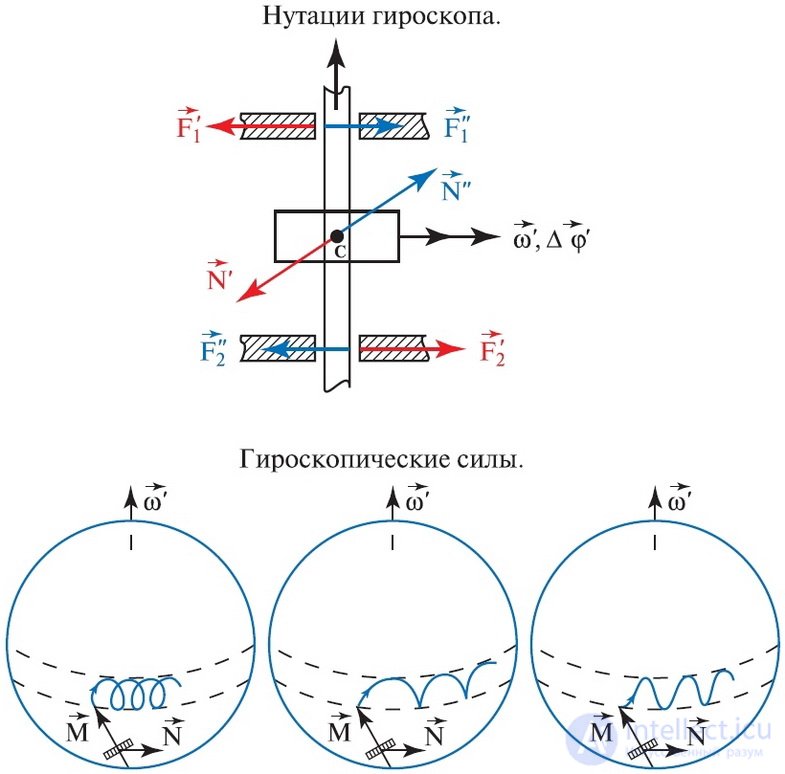
Рис. 7.24. Нутации гироскопа
Угловая скорость прецессии в рассматриваемом случае равна
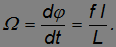
Отметим важное свойство гироскопа — его безынерционность, заключающееся в том, что после прекращения действия внешней силы вращение оси фигуры прекращается.
Влияние гироскопических сил в технике иллюстрируется следующими рисунками.
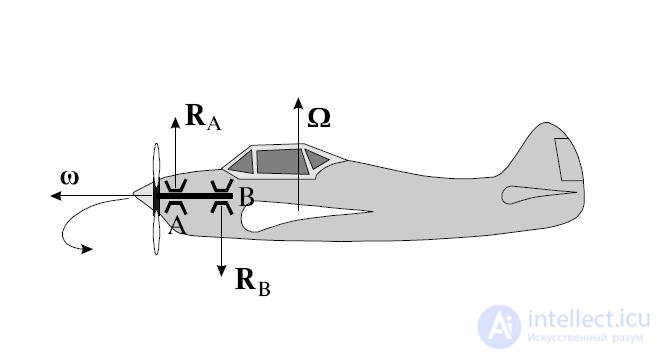
Рис. 7.25. Гироскопические силы,действующие на самолет при вращении винта
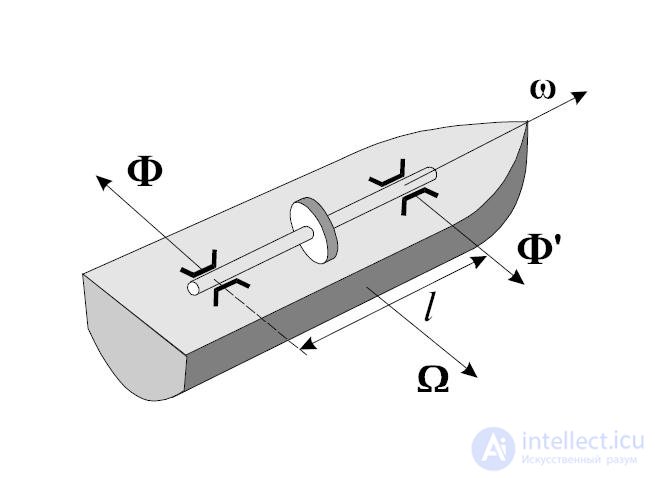
Рис. 7.26. Перевертывание волчка под действием гироскопических сил
Рис. 7.27. Как поставить яйцо «на попа»
Приложение
О принципе работы колеса
Раз уж мы много говорили в этой главе о вращении тел, остановимся на самом великом и важном открытии человечества — изобретении колеса. Всем известно, что волочить груз гораздо труднее, чем перевозить его на колесах. Встает вопрос, почему? Колесо, играющее огромную роль в современной технике, по праву считается одним из гениальнейших изобретений человечества.
Передвижение груза с помощью катка. Прототипом колеса был каток, подкладываемый под груз. Его первые применения теряются во мгле веков. Прежде чем разбираться с колесом, поймем принцип действия катка. Для этого рассмотрим пример.
Пример. Груз массой M положен на цилиндрический каток массой 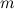 и радиусом
и радиусом  , который может двигаться по плоскому горизонтальному настилу. К грузу приложена горизонтальная сила
, который может двигаться по плоскому горизонтальному настилу. К грузу приложена горизонтальная сила 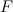 (рис. 7.28). Найдем ускорения груза и катка. Силой трения качения пренебречь. Считать, что движение системы происходит без проскальзывания.
(рис. 7.28). Найдем ускорения груза и катка. Силой трения качения пренебречь. Считать, что движение системы происходит без проскальзывания.
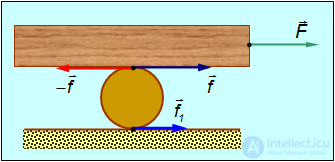
Рис. 7.28. Передвижение груза с помощью катка
Обозначим 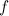 силу трения между катком и грузом и
силу трения между катком и грузом и 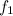 — между катком и настилом. За положительное направление примем направление внешней силы
— между катком и настилом. За положительное направление примем направление внешней силы 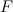 . Тогда положительным значениям
. Тогда положительным значениям 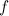 и
и 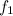 соответствуют направления сил трения, показанные на рис. 7.28.
соответствуют направления сил трения, показанные на рис. 7.28.
Таким образом, на груз действуют силы 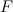 и
и 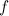 , а на каток — силы
, а на каток — силы 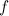 и
и 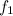 . Обозначим a ускорение груза и a1 — ускорение катка. Кроме того, каток вращается по часовой стрелке с угловым ускорением
. Обозначим a ускорение груза и a1 — ускорение катка. Кроме того, каток вращается по часовой стрелке с угловым ускорением  .
.
Уравнения поступательного движения принимают вид:
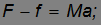
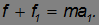
Уравнение вращательного движения катка записывается так:
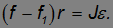
Обратимся теперь к условиям отсутствия проскальзывания. Из-за вращения катка его нижняя точка имеет линейное ускорение 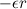 и, кроме того, участвует в поступательном движении с ускорением
и, кроме того, участвует в поступательном движении с ускорением 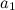 . В отсутствие проскальзывания между катком и настилом полное ускорение нижней точки катка должно быть равно нулю, так что
. В отсутствие проскальзывания между катком и настилом полное ускорение нижней точки катка должно быть равно нулю, так что
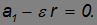
Верхняя точка катка приобретает из-за вращения противоположно направленное линейное ускорение 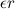 и то же ускорение
и то же ускорение 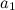 поступательного движения. Чтобы не было проскальзывания между катком и грузом, полное ускорение верхней точки должно быть равно ускорению груза:
поступательного движения. Чтобы не было проскальзывания между катком и грузом, полное ускорение верхней точки должно быть равно ускорению груза:
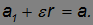
Из полученных уравнений для ускорений следует, что ускорение катка в два раза меньше ускорения груза:
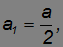
и, соответственно,
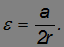
Из непосредственного опыта каждый знает, что каток действительно отстает от груза.
Подставляя соотношения для ускорений в уравнения движения и решая их относительно неизвестных  ,
, 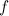 ,
, 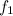 , получаем следующие выражение для ускорения груза
, получаем следующие выражение для ускорения груза
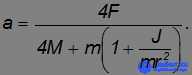
Обе силы трения 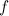 и
и 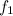 оказываются при этом положительными, так что на рис. 12 их направления выбраны правильно:
оказываются при этом положительными, так что на рис. 12 их направления выбраны правильно:
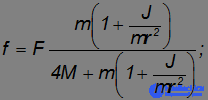
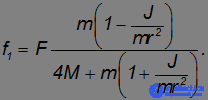
Как видно, радиус катка особой роли не играет: отношение 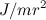 зависит только от его формы. При данных массе
зависит только от его формы. При данных массе 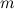 и радиусе
и радиусе  момент инерции катка максимален, когда каток представляет собой трубу:
момент инерции катка максимален, когда каток представляет собой трубу: 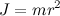 . В этом случае сила трения между катком и настилом отсутствует (
. В этом случае сила трения между катком и настилом отсутствует (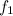 = 0) а уравнения для ускорения груза и силы трения между грузом и катком принимают вид:
= 0) а уравнения для ускорения груза и силы трения между грузом и катком принимают вид:
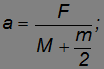
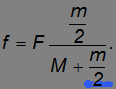
При уменьшении массы катка сила трения уменьшается, ускорение груза увеличивается — груз легче перемещать.
В случае катка-цилиндра (бревна) 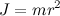 /2 и мы находим силы трения
/2 и мы находим силы трения
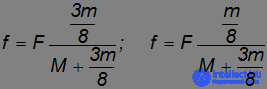
и ускорение груза.
Сравнивая с результатами для катка-трубы, видим, что эффективно масса катка как бы уменьшилась: ускорение груза возрастает при прочих равных условиях.
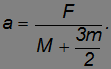
Главный итог рассмотренного примера: ускорение отлично от нуля (то есть груз начинает двигаться) при сколь угодно малой внешней силе. При волочении же груза по настилу для его смещения необходимо приложить как минимум силу 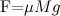 .
.
Второй вывод: ускорение вовсе не зависит от величины трения между частями данной системы. Коэффициент трения 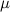 не вошел в найденные решения, он появится только в условиях отсутствия проскальзывания, которые сводятся к тому, что приложенная сила
не вошел в найденные решения, он появится только в условиях отсутствия проскальзывания, которые сводятся к тому, что приложенная сила 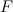 не должна быть слишком велика.
не должна быть слишком велика.
Полученный результат, что каток как бы полностью «уничтожает» силу трения, не удивителен. Действительно, в отсутствие относительного перемещения соприкасающихся поверхностей силы трения не совершают работы. На самом деле каток «заменяет» трение скольжения на трение качения, которым мы пренебрегли. В реальном случае минимальная сила, необходимая для движения системы, отлична от нуля, хотя и гораздо меньше, чем при волочении груза по настилу. В современной технике принцип действия катка реализуется в шарикоподшипниках.
Качественное рассмотрение работы колеса. Разобравшись с катком, перейдем к колесу. Первое колесо в виде деревянного диска, насаженного на ось, появилось, по-видимому, в IV тысячелетии до н.э. в цивилизациях Древнего Востока. Во II тыс. до н.э. конструкция колеса совершенствуется: появляются спицы, ступица и гнутый обод. Изобретение колеса дало гигантский толчок развитию ремесел и транспорта. Однако многие не понимают самого принципа действия колеса. В ряде учебников и энциклопедий можно найти неверное утверждение, что колесо, подобно катку, также дает выигрыш, заменяя силу трения скольжения на силу трения качения. Иногда приходится слышать ссылки на использование смазки или подшипников, но дело не в этом, поскольку колесо с очевидностью появилось раньше, чем додумались до смазки (и, тем более, подшипников).
Действие колеса проще всего понять, исходя из энергетических соображений. Древние повозки устроены просто: кузов прикрепляется к деревянной оси радиусом  (общая масса кузова с осью равна M). На ось насаживаются колеса массой
(общая масса кузова с осью равна M). На ось насаживаются колеса массой 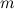 и радиусом R (рис. 7.29).
и радиусом R (рис. 7.29).
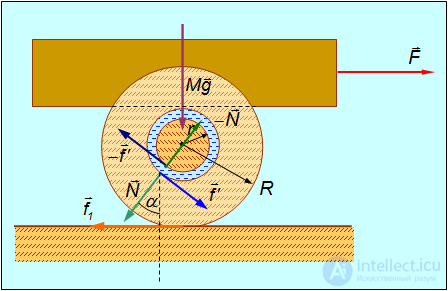
Рис. 7.29. Передвижение движение груза с помощью колеса
Предположим, что такую повозку везут по деревянному же настилу (тогда во всех соприкасающихся местах имеем тот же коэффициент трения 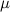 ). Сначала заклиним колеса и, действуя силой
). Сначала заклиним колеса и, действуя силой 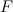 , протащим повозку на расстояние s. Поскольку повозка скользит по настилу, сила трения достигает своего максимально возможного значения
, протащим повозку на расстояние s. Поскольку повозка скользит по настилу, сила трения достигает своего максимально возможного значения
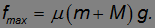
Работа против этой силы равна
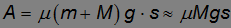
(так как обычно масса колес много меньше массы повозки 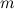 <<M).
<<M).
Освободим теперь колеса и снова протащим повозку на то же расстояние s. Если колеса не скользят по настилу, то в нижней точке колеса сила трения не совершает работы. Но трение скольжения возникает между осью и колесом в нижней части оси радиусом  . Там тоже имеется сила нормального давления. Она будет несколько отличаться от прежней за счет веса колес и других причин, которые мы обсудим ниже, но при небольшой массе колес и небольшом коэффициенте трения можно считать ее примерно равной
. Там тоже имеется сила нормального давления. Она будет несколько отличаться от прежней за счет веса колес и других причин, которые мы обсудим ниже, но при небольшой массе колес и небольшом коэффициенте трения можно считать ее примерно равной 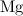 . Поэтому между осью и колесом действует та же самая сила трения
. Поэтому между осью и колесом действует та же самая сила трения
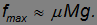
Подчеркнем еще раз: колесо само по себе не уменьшает силу трения. Но работа A' против этой силы будет теперь гораздо меньше, чем в случае волочения повозки с заклиненными колесами. Действительно, когда повозка проходит расстояние S, ее колеса совершают 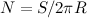 оборотов. Значит, трущиеся об ось колеса поверхности сдвинутся друг относительно друга на меньшее расстояние
оборотов. Значит, трущиеся об ось колеса поверхности сдвинутся друг относительно друга на меньшее расстояние 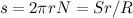 . Поэтому работа против сил трения также будет в соответствующее число раз меньше:
. Поэтому работа против сил трения также будет в соответствующее число раз меньше:
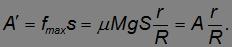
Таким образом, надев колеса на оси, мы уменьшаем не силу трения, как в случае с катком, а путь, на котором она действует. Скажем, колесо радиусом R = 0,5 м и осью радиусом  = 2 см уменьшает работу на 96 %. С остальными 4 % успешно справляются смазка и подшипники, уменьшающие само трение (смазка, кроме того, предотвращает износ ходовой части повозки). Теперь понятно, почему в старых экипажах и боевых колесницах делали такие большие колеса. Современные продуктовые коляски в супермаркетах могут катиться лишь благодаря подшипникам.
= 2 см уменьшает работу на 96 %. С остальными 4 % успешно справляются смазка и подшипники, уменьшающие само трение (смазка, кроме того, предотвращает износ ходовой части повозки). Теперь понятно, почему в старых экипажах и боевых колесницах делали такие большие колеса. Современные продуктовые коляски в супермаркетах могут катиться лишь благодаря подшипникам.
Из полученной формулы для работы при качении следует, что при  = R (колеса без оси, вмонтированные в корпус и трущиеся об него) будет совершена та же работа, что и при волочении повозки. Весь выигрыш заключен в отношении радиусов
= R (колеса без оси, вмонтированные в корпус и трущиеся об него) будет совершена та же работа, что и при волочении повозки. Весь выигрыш заключен в отношении радиусов  /R, то есть колесо — по сути дела рычаг непрерывного действия с плечами
/R, то есть колесо — по сути дела рычаг непрерывного действия с плечами  и R. Благодаря «сворачиванию» рычага в окружность его не надо возвращать в начальное положение: это достигается автоматически. Трудно представить себе техническое изобретение, более гениальное по простоте и эффективности!
и R. Благодаря «сворачиванию» рычага в окружность его не надо возвращать в начальное положение: это достигается автоматически. Трудно представить себе техническое изобретение, более гениальное по простоте и эффективности!
Количественная теория колеса. Рассмотрим силы, действующие на нашу повозку (см. рис. 7.29).
Силы, действующие на колесо: сила трения 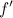 со стороны оси, сила нормального давления
со стороны оси, сила нормального давления 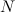 со стороны оси, сила трения
со стороны оси, сила трения 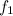 со стороны настила. Эти силы показаны на рис. 7.29 соответственно синей, зеленой и оранжевой стрелками. Заметим, что мы не предполагаем, что ось соприкасается с колесом в своей нижней точке: угол
со стороны настила. Эти силы показаны на рис. 7.29 соответственно синей, зеленой и оранжевой стрелками. Заметим, что мы не предполагаем, что ось соприкасается с колесом в своей нижней точке: угол 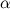 описывает смещение назад точки соприкосновения оси с колесом (соответственно, точки приложения сил
описывает смещение назад точки соприкосновения оси с колесом (соответственно, точки приложения сил 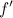 ,
, 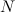 ). Значение угла
). Значение угла 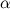 также должно быть найдено из решений уравнений движения. Кроме того, на колесо действует сила тяжести
также должно быть найдено из решений уравнений движения. Кроме того, на колесо действует сила тяжести 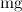 и нормальное давление
и нормальное давление 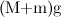 со стороны настила, но они сейчас нам не важны и на рисунке не показаны.
со стороны настила, но они сейчас нам не важны и на рисунке не показаны.
Выбирая ось х в горизонтальном направлении, а ось у — в вертикальном, записываем проекцию уравнения поступательного движения колеса на ось x :
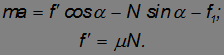
Предполагая отсутствие проскальзывания в точке соприкосновения колеса с настилом (то есть 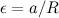 ), записываем уравнение вращательного движения колеса:
), записываем уравнение вращательного движения колеса:
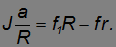
Силы, действующие на повозку (показаны соответственно красной, фиолетовой, темно-синей и темно-зеленой стрелками на рис. 7.29): внешняя сила 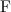 , сила тяжести
, сила тяжести 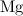 и силы
и силы 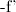 ,
, 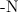 со стороны оси. Записываем уравнения поступательного движения повозки в проекциях на оси x, y :
со стороны оси. Записываем уравнения поступательного движения повозки в проекциях на оси x, y :
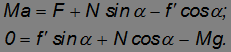
Мы имеем пять уравнений для пяти неизвестных:  ,
, 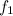 ,
, 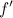 ,
, 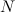 ,
, 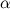 . Их все можно найти, решая систему уравнений. Мы хотим получить лишь ответ на вопрос: при какой минимальной силе
. Их все можно найти, решая систему уравнений. Мы хотим получить лишь ответ на вопрос: при какой минимальной силе 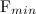 повозка сдвинется с места? Для этого надо положить
повозка сдвинется с места? Для этого надо положить 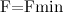 , при этом ускорение
, при этом ускорение  = 0. Имеем тогда систему уравнений:
= 0. Имеем тогда систему уравнений:
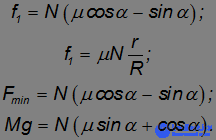
Здесь мы уже учли выражение закона трения скольжения. Из двух первых уравнений следует:
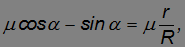
откуда можно найти тригонометрические функции угла 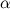 :
:
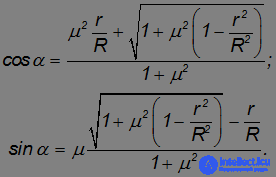
Тогда из двух последних уравнений следует искомое выражение:
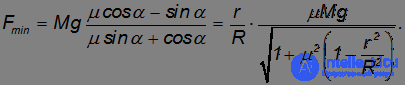
Любопытно, что масса колес не вошла в конечный ответ для 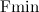 .
.
В предельном случае  = R имеем
= R имеем 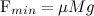 , что соответствует, в сущности, отсутствию колес и перетаскивание повозки волоком. В обратном предельном случае
, что соответствует, в сущности, отсутствию колес и перетаскивание повозки волоком. В обратном предельном случае
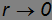
минимальная сила также стремится к нулю. При малых коэффициентах трения квадратный корень в знаменателе приближенно равен единице, и
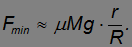
Выше мы качественно получили этот результат из энергетических соображений.
Исследование, описанное в статье про динамика твердого тела, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое динамика твердого тела, гироскоп, принцип работы колеса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики