Лекция
Привет, Вы узнаете о том , что такое механика жидкостей и газов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое механика жидкостей и газов, закон паскаля (гидростатики), уравнение непрерывности, движение тел в среде с сопротивлением, турбулентность, ламинарность , настоятельно рекомендую прочитать все из категории Физические основы механики.
В механике с большой степенью точности жидкости и газы рассматриваются как сплошные среды, непрерывно распределенные в занятой ими части пространства. Плотность жидкости слабо зависит от давления. Плотность же газов от давления зависит существенным образом. Однако из опыта известно, что сжимаемостью газа, как и жидкости, во многих задачах можно пренебречь и пользоваться единым понятием несжимаемой жидкости, плотность которой всюду одинакова. Гидростатика — наука древняя. Основываясь, например, на свойствах равновесия несжимаемой жидкости, французский ученый Б. Паскаль установил закон сообщающихся сосудов (известный, правда, еще Леонардо да Винчи). Исследования Паскаля по гидростатике были опубликованы в 1663 г., уже после его смерти. С них мы и начнем эту главу.
Утверждение, известное как закон Паскаля или закон гидростатики, но в равной мере справедливое и для газов, гласит:
Жидкость, находящаяся в замкнутом сосуде, передает производимое на нее давление по всем направлениям одинаково.
Данное свойство жидкости можно продемонстрировать с помощью прибора, называемого шаром Паскаля (рис. 9.1).
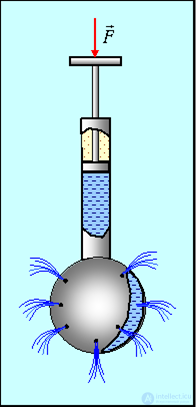
Рис. 9.1. Шар Паскаля
Проведем мысленно в некотором объеме жидкости, находящемся в равновесии, площадку 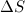 . Отдельные частицы жидкости действуют друг на друга и, в частности, на площадку
. Отдельные частицы жидкости действуют друг на друга и, в частности, на площадку 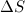 с силой, зависящей от степени сжатия. Это воздействие характеризуется давлением
с силой, зависящей от степени сжатия. Это воздействие характеризуется давлением
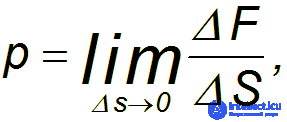
где 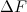 — равнодействующая всех сил, с которыми жидкость действует на площадку.
— равнодействующая всех сил, с которыми жидкость действует на площадку.
В системе СИ единицей давления является паскаль (Па):
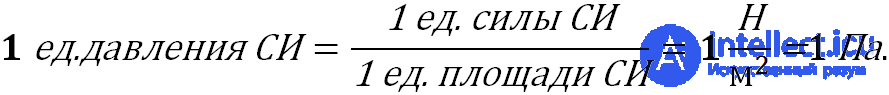
Один паскаль — давление, производимое силой один ньютон, равномерно распределенной по нормальной к ней поверхности площадью 1 м2.
Например, если булавка вдавливается в поверхность стола силой 10 Н, а площадь ее острия 0,05 мм2, то давление булавки на стол равно

На рис. 9.2 показаны характерные масштабы давлений, встречающихся в природе.
Рис. 9.2. Масштабы давлений, встречающихся в окружающем мире
Обратим внимание: давление — скалярная величина, для него неприменимо понятие направления. Сила же, с которой жидкость давит на элементарную площадку 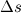 , всегда направлена по нормали к площадке.
, всегда направлена по нормали к площадке.
Если внутри жидкости поместить тонкую пластинку площадью S, то со стороны жидкости на нее будет действовать сила давления, перпендикулярная к ее поверхности (рис. 9.3).

Рис. 9.3. Сила давления в жидкости
Действительно, если бы сила была направлена не под прямым углом к выбранной площадке, то ее касательная составляющая из-за отсутствия сопротивления сдвигу привела бы жидкость в движение, что противоречит условию неподвижности.
Одно из проявлений закона Паскаля можно наблюдать в гидравлическом прессе (рис. 9.4).
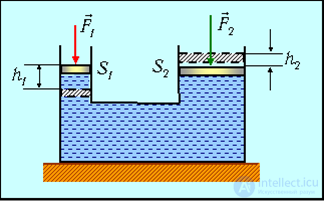
Рис. 9.4. Принцип работы гидравлического пресса
Два сообщающихся сосуда заполнены жидкостью и закрыты поршнями различной площади. По закону Паскаля, давления под поршнями одинаковы p1 = p2, то есть

или

Таким образом, сила давления второго поршня больше силы давления первого во столько раз, во сколько площадь второго поршня больше площади первого. Гидравлический пресс — простой механизм, позволяющий развивать колоссальные силы, используемые для прессования различных изделий из металлов и пластмасс. Обозначим h1 и h2 — ходы поршней. Вследствие практической несжимаемости объемы жидкости, перешедшей из одного цилиндра в другой, одинаковы:
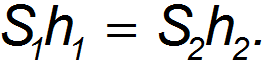
Работы, совершаемые силами F1(2) за один ход, вычисляются как

и

так что их отношение будет
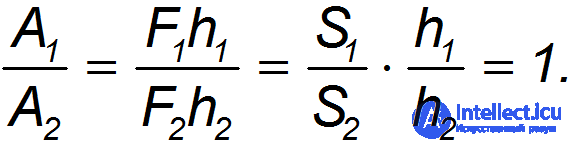
Как и следовало ожидать, пресс дает выигрыш в силе, но не в совершаемой работе.
На том же принципе основано устройство гидравлического подъемника (рис. 9.5). Обратите внимание на то, что площадь поперечного сечения первого цилиндра, в котором возвратно-поступательно движется поршень, накачивающий масло, значительно меньше площади поперечного сечения цилиндра, который направляет движение второго поршня. Второй поршень передает усилие на шток, соединенный жестко с платформой, на которой поднимается груз — автомобиль. При одинаковом давлении масла в системе силы давления, с которыми масло действует на поршни, значительно отличаются.
Открывание вентиля 3 приводит к тому, что под действием давления масло перетекает в бак для его хранения.
Рис. 9.5. Работа гидравлического подъемника
Определим давление внутри жидкости, считая ее несжимаемой, то есть считая ее плотность неизменной независимо от глубины. Пусть на жидкость в сосуде действует внешнее давление p0. Выделим мысленно в жидкости вертикальный цилиндр с поперечным сечением S и высотой h (рис. 9.6).

Рис. 9.6. Давление жидкости в поле сил тяжести
На верхний слой жидкости действует внешнее давление p0, которое также передается и другим слоям жидкости. К этому давлению в нижележащих слоях добавляется давление, создаваемое весом сло`в жидкости, расположенных выше. На верхнее основание цилиндра действует сила F0 = p0S, на нижнее основание F = pS, где p — давление на глубине h. Кроме того, вертикально вниз действует сила тяжести столба жидкости, находящейся в объеме цилиндра:

где ρ — плотность жидкости, hS — ее объем.
Запишем условие равновесия выделенного столба жидкости:
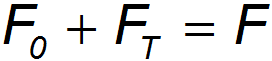
или
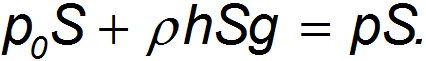
Следовательно, давление в жидкости на глубине h будет равно
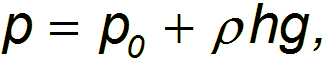
где ρgh — гидростатическое давление жидкости, обусловленное ее тяжестью.
Согласно полученной формуле, сила давления на нижние слои жидкости будет больше, чем на верхние. Поэтому на тело, погруженное в жидкость, действует выталкивающая сила, называемая силой Архимеда. Погрузим в жидкость на глубину h параллелепипед с площадью основания S и высотой ребра a (рис. 9.7).
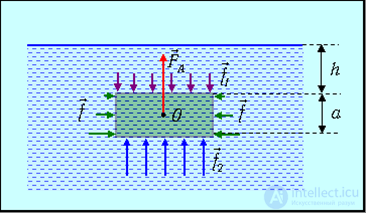
Рис. 9.7. Сила Архимеда, действующая на тело, погруженное в однородную жидкость
Давление на глубине h равно

и потому на верхнее основание действует сила

На глубине h+a давление равно
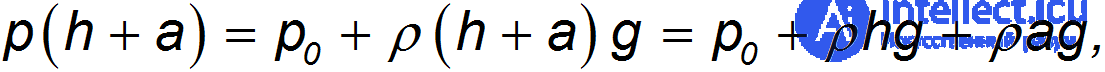
и потому на нижнее основание действует сила

Равнодействующая этих двух сил направлена вверх и равна по величине

Здесь Sa = V — объем погруженной части тела, m = pV — жидкости (газа) того же объема.
Полученное уравнение представляет математическую формулировку закона Архимеда:
На тело, погруженное в жидкость (газ), действует выталкивающая сила, равная весу вытесненной телом жидкости (газа).

Рис. 9.8. Иллюстрация закона Архимеда
Рассмотрим теперь движение жидкости. Самый простой случай — так называемое стационарное течение. Нет никакого противоречия в употреблении слова «стационарный» рядом со словом «течение», которое подразумевает движение элементов жидкости.
Стационарное течение — это течение, при котором скорость жидкости в каждой данной точке остается постоянной как по величине, так и по направлению.
Элементы жидкости приходят и уходят, но в данной точке каждый вновь пришедший элемент приобретает ту скорость, которая этой точке соответствует. Поэтому стационарное течение можно характеризовать полем скоростей, задавая векторную функцию v(r) от пространственных координат. Графически поле скоростей изображается с помощью линий тока.
Ориентированная линия, касательная к которой в каждой точке совпадает по направлению с вектором скорости в данной точке пространства, называется линией тока.
На рис. 9.9 показана линия тока в области течения жидкости.
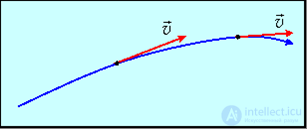
Рис. 9.9. Линия тока
Если вспомнить то, что мы знаем из школьного курса физики об электричестве, то можно сказать, что линии тока — это аналог силовых линий.
Условимся проводить линии тока так, чтобы густота их (которая характеризуется отношением числа линий  к величине перпендикулярной к ним площади
к величине перпендикулярной к ним площади 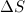 , через которую они проходят) была пропорциональна величине скорости в данном месте. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Для стационарного течения форма и расположение линий тока со временем не изменяются.
, через которую они проходят) была пропорциональна величине скорости в данном месте. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Для стационарного течения форма и расположение линий тока со временем не изменяются.
Рассмотрим какую-либо трубку тока. Всюду далее полагаем площадь сечения трубки достаточно малой, так что можно считать скорость жидкости одинаковой во всех точках сечения. За время dt через произвольное ее сечение S проходит объем жидкости Svdt (рис. 9.10–1).

Рис. 9.10 Трубки тока
Выберем два ее сечения S1 и S2 (рис. 9–2). За время dt через сечение S1 пройдет объем жидкости S1v1dt, где v1 — скорость течения жидкости в точках сечения S1. Аналогично, через сечение S2 за то же время dt пройдет объем жидкости S2v2dt, где v2 — скорость течения жидкости в точках сечения S2. Из условия несжимаемости жидкости следует равенство объемов жидкости, вошедших в область между сечениями S1, S2 и вышедших из него:

Следовательно,
В несжимаемой жидкости величина Sv в любом сечении одной и той же трубки одинакова,другими словами,эта величина постоянна вдоль трубки тока:
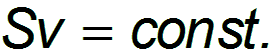
Это соотношение — одна из форм теоремы о непрерывности струи. Данная теорема выражает собой факт несжимаемости жидкости.
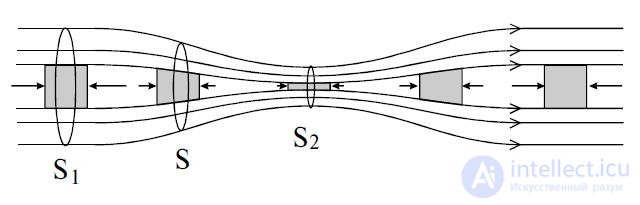
Рис. Об этом говорит сайт https://intellect.icu . 9.11. Скорость струи в различных сечениях трубки
Теорема о непрерывности струи применима к реальным жидкостям, а также к газам, в том случае, если сжимаемостью их можно пренебречь. Прямое следствие теоремы — широко известный факт: в месте сужения трубы скорость потока возрастает. Более того, аналогичная теорема есть и в теории электромагнетизма, и там она связана с сохранением электрического заряда.
Пример. Оценим пропускную способность одного ряда участка автомагистрали. Учтем, что «Правила дорожного движения» рекомендуют держать дистанцию L между автомобилями, которая в метрах численно равна половине скорости движения, выраженной в км/час.
В этой задаче мы в сущности тоже имеем дело с уравнением непрерывности — при отсутствии «пробки» на дороге через каждое ее сечение должно проходить одинаковое количество автомобилей. Поток автомобилей равен
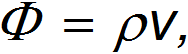
где v — средняя скорость движения, а ρ — линейная «плотность» автомобилей на дороге, то есть число машин на единицу длины. Если l — средняя длина автомобиля, a L — средняя дистанция между ними, то
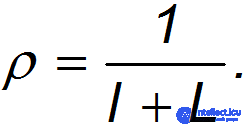
Рекомендацию «Правил дорожного движения» математически можно выразить в виде формулы:
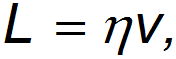
где
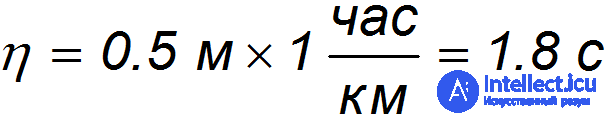
— «коэффициент безопасности». В итоге приходим к выражению:
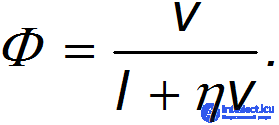
Для численной оценки примем l = 3 м, a v = 60 км/час = 16,67 м/с (допустимая скорость движения в городах). Получаем тогда:
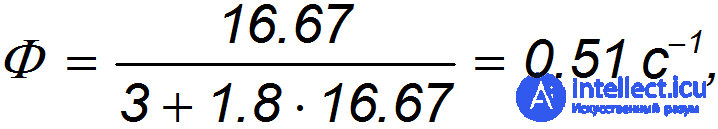
то есть каждый ряд способен пропустить 30 машин в минуту.
При повышении скорости движения до v = 90 км/час = 25 м/с пропускная способность возрастает совершенно незначительно: в этом случае находим

Даже в пределе бесконечно большой скорости движения

предельное значение потока
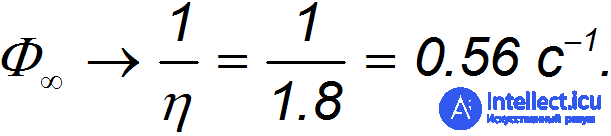
При снижении скорости движения, скажем, до v = 30 км/час = 8,33 м/с пропускная способность станет

Гораздо более «эффективным» является несоблюдение дистанции. Скажем, при дистанции L, равной длине l корпуса автомобиля, и скорости движения v = 30 км/час, получаем для потока:
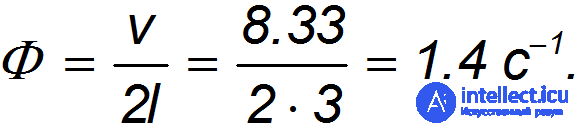
Но вряд ли повышение пропускной способности магистрали даже в три раза должно достигаться за счет уменьшения безопасности движения.
При течении жидкости ее отдельные слои в общем случае текут с разными скоростями, скользят друг относительно друга, вследствие чего между ними возникают силы трения. Эти силы называют силами внутреннего трения. Они возникают не только в жидкостях, но и в газах.
Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.
Выделим в стационарно текущей идеальной жидкости трубку тока, ограниченную сечениями 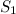 и
и 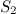 , по которой слева направо течет жидкость (рис. 9.12). Пусть в месте сечения
, по которой слева направо течет жидкость (рис. 9.12). Пусть в месте сечения 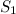 заданы: скорость течения
заданы: скорость течения  , давление
, давление 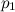 и высота
и высота 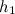 , на которой расположено это сечение. Аналогично, в месте сечения
, на которой расположено это сечение. Аналогично, в месте сечения 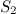 заданы скорость течения
заданы скорость течения  , давление
, давление 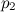 и высота
и высота 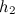 .
.

Рис. 9.12. К выводу уравнения Бернулли
За время 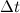 объем жидкости переместится вдоль трубки тока, причем сечение
объем жидкости переместится вдоль трубки тока, причем сечение 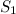 переместится в положение
переместится в положение 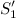 , пройдя путь
, пройдя путь 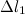 , сечение
, сечение 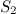 переместится в положение
переместится в положение 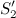 , пройдя путь
, пройдя путь  . В силу уравнения непрерывности струи заштрихованные объемы будут иметь одинаковую величину:
. В силу уравнения непрерывности струи заштрихованные объемы будут иметь одинаковую величину:  .
.
Энергия каждой частицы жидкости слагается из ее кинетической энергии и потенциальной энергии в поле сил тяжести. Полная энергия потока, протекающего за время 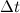 через сечение
через сечение 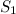 , равна
, равна
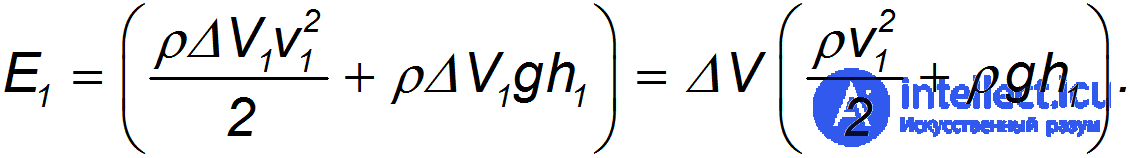
Аналогичное выражение для энергии потока имеем для сечения 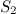 :
:
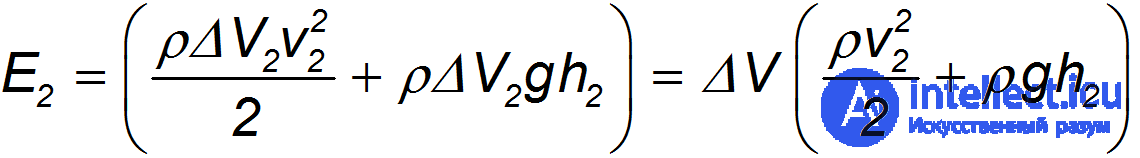
При стационарном течении между сечениями 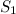 и
и 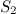 энергия не накапливается. В идеальной жидкости силы трения отсутствуют, так что механическая энергия никуда не исчезает. Следовательно, изменение полной энергии жидкости равно работе, совершенной внешними силами
энергия не накапливается. В идеальной жидкости силы трения отсутствуют, так что механическая энергия никуда не исчезает. Следовательно, изменение полной энергии жидкости равно работе, совершенной внешними силами

Силы давления на боковую поверхность трубки тока перпендикулярны в каждой точке к направлению перемещения частиц, вследствие чего работы не совершают. Отлична от нуля лишь работа сил давления, приложенных к сечениям 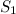 и
и 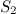 . Эта работа равна
. Эта работа равна

Приравнивая изменение энергии потока 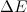 работе сил давления
работе сил давления 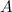 , находим:
, находим:
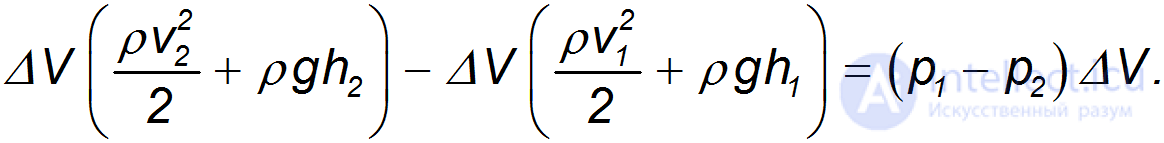
Сократив на 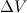 и перенеся члены с одинаковыми индексами в одну часть равенства, получаем:
и перенеся члены с одинаковыми индексами в одну часть равенства, получаем:
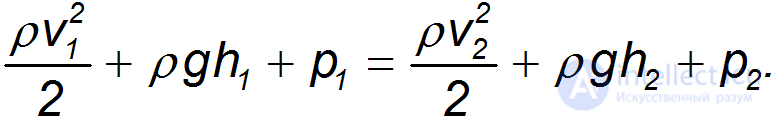
Сечения 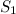 и
и 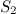 были взяты совершенно произвольно. Поэтому можно утверждать, что
были взяты совершенно произвольно. Поэтому можно утверждать, что
В стационарно текущей идеальной несжимаемой жидкости в любом сечении трубки тока величина
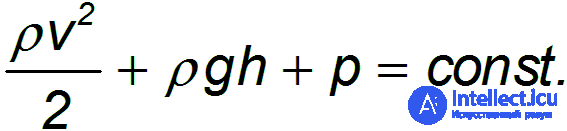
имеет одно и то же значение, другими словами, вдоль трубки тожа эта величина постоянна
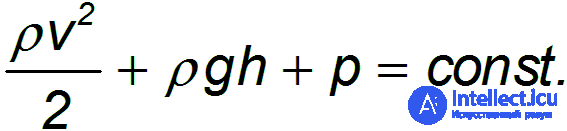
Полученное нами соотношение называется уравнением Бернулли. Это уравнение выражает собой закон сохранения механической энергии при стационарном течении несжимаемой идеальной жидкости.
В частном случае горизонтального течения жидкости 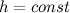 уравнение Бернулли принимает вид
уравнение Бернулли принимает вид
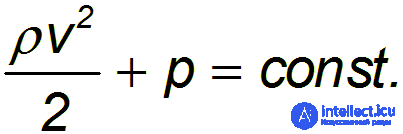
Из уравнения непрерывности

следует, что в месте сужения потока его скорость возрастает, а из уравнения Бернулли — что в этом месте падает давление.

Рис. 9.13. Скорости жидкости и давление в зависимости от сечения трубки
Когда идущие параллельными курсами корабли находятся слишком близко друг к другу, давление между ними падает и давление внешнего потока их сближает, и может привести к столкновению судов.
Пример. В сосуде проделано небольшое отверстие. Высота жидкости над отверстием равна 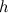 . Найдем скорость вытекающей струи.
. Найдем скорость вытекающей струи.
Применим уравнение Бернулли. В качестве сечения 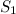 возьмем поверхность жидкости, а за сечение
возьмем поверхность жидкости, а за сечение 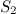 примем проделанное отверстие. Давления в обоих сечениях можно считать постоянными (и равными атмосферному). Скоростью жидкости в сечении
примем проделанное отверстие. Давления в обоих сечениях можно считать постоянными (и равными атмосферному). Скоростью жидкости в сечении 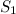 можно пренебречь (если площадь сосуда много больше площади отверстия:
можно пренебречь (если площадь сосуда много больше площади отверстия: 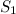 >>
>> 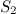 ) Тогда имеем:
) Тогда имеем:

где 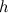 — высота сечения
— высота сечения 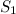 над сечением
над сечением 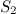 (то есть уровень жидкости над отверстием), a
(то есть уровень жидкости над отверстием), a  — скорость истечения жидкости из отверстия. Получаем в итоге:
— скорость истечения жидкости из отверстия. Получаем в итоге:
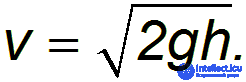
Указанное соотношение называется формулой Торричелли. Заметим, что скорость истечения струи равна скорости свободного падения тела с той же высоты. Это не удивительно, так как в основе обоих результатов лежит закон сохранения энергии при движении в однородном поле сил тяжести.
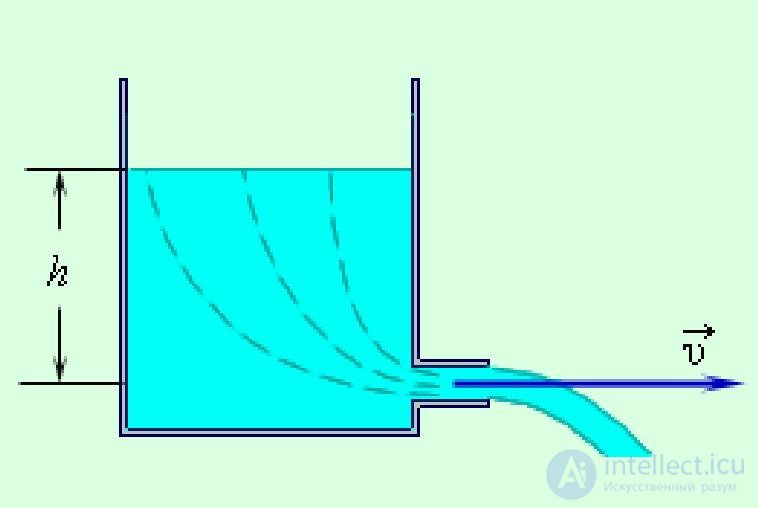
Рис. 9.14. Истечение жидкости из отверстия
Выводя уравнение Бернулли, мы пренебрегли сжимаемостью жидкости. Что касается газов, их сжимаемость намного больше, чем у жидкостей. Получим оценку применимости уравнения Бернулли к течению газов. Величина  , называемая динамическим давлением, должна быть мала по сравнению со статическим давлением
, называемая динамическим давлением, должна быть мала по сравнению со статическим давлением  . Тогда колебания давления вследствие течения газа будут невелики и его сжимаемостью можно пренебречь. Следовательно, критерием применимости уравнения Бернулли к газам служит неравенство
. Тогда колебания давления вследствие течения газа будут невелики и его сжимаемостью можно пренебречь. Следовательно, критерием применимости уравнения Бернулли к газам служит неравенство
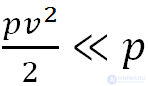
или
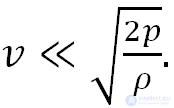
Приведем численную оценку. При нормальных условиях давление воздуха приблизительно равно 105 Па, а плотность воздуха 1,29 кг/м3. Отсюда
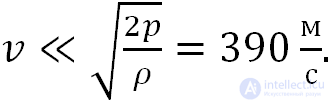
Это число близко к скорости звука и отличается от нее только коэффициентом 2 под знаком корня: в выражении для скорости звука под знаком корня стоит показатель адиабаты 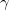 , равный для воздуха при комнатных температурах 1,4. Как будет видно позже, это не случайно, поэтому критерий применимости к газу приближения «несжимаемой жидкости», в котором он считается несжимаемым, можно сформулировать так. Можно пренебречь сжимаемостью газа при скоростях его течения много меньших скорости звука в этом газе:
, равный для воздуха при комнатных температурах 1,4. Как будет видно позже, это не случайно, поэтому критерий применимости к газу приближения «несжимаемой жидкости», в котором он считается несжимаемым, можно сформулировать так. Можно пренебречь сжимаемостью газа при скоростях его течения много меньших скорости звука в этом газе:
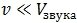
При таких скоростях мы можем применять уравнение Бернулли к газам с тем же успехом, что и к жидкостям.
Со времен опытов Галилея на Пизанской башне известно, что все тела падают в поле силы тяжести с одинаковым ускорением g.
Однако каждодневная практика указывает на другое: легкое перышко падает медленнее тяжелого металлического шарика. Понятна и причина этого — сопротивление воздуха.
Уравнения движения. Если ограничиться случаем поступательного движения невращающихся тел в неподвижной среде с сопротивлением, то сила сопротивления будет направлена против скорости. В векторном виде ее можно записать как
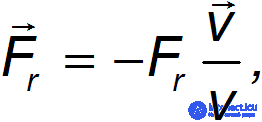
где 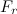 — абсолютная величина этой силы, a
— абсолютная величина этой силы, a  — модуль скорости тела. Учет сопротивления среды меняет вид уравнений движения тела, брошенного под углом к горизонту:
— модуль скорости тела. Учет сопротивления среды меняет вид уравнений движения тела, брошенного под углом к горизонту:
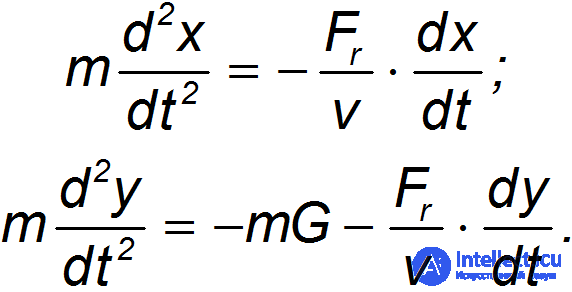
В приведенных уравнениях учтена также выталкивающая сила Архимеда, действующая на тело: ускорение свободного падения g заменено на меньшую величину
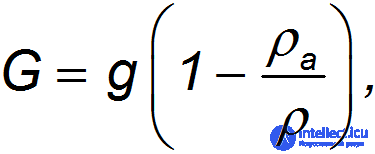
где  — плотность среды (для воздуха
— плотность среды (для воздуха  = 1.29 кг/м3), а
= 1.29 кг/м3), а  — средняя плотность тела.
— средняя плотность тела.
Действительно, вес  тела в среде уменьшается на величину выталкивающей силы Архимеда
тела в среде уменьшается на величину выталкивающей силы Архимеда
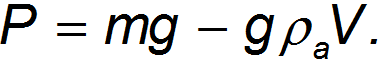
Выражая объем  тела через его среднюю плотность
тела через его среднюю плотность
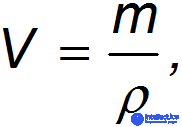
приходим к выражению

При наличии сопротивления воздуха скорость падающего тела не может расти безгранично. В пределе она стремится к некоторому установившемуся значению, которое зависит от характеристик тела. Если тело достигло установившейся скорости падения 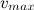 , то из уравнений движения следует, что сила сопротивления равна весу тела (с учетом архимедовой силы):
, то из уравнений движения следует, что сила сопротивления равна весу тела (с учетом архимедовой силы):

Сила сопротивления 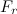 как мы вскоре убедимся, есть функция скорости падения. Стало быть, полученное выражение для силы сопротивления представляет собой уравнение для определения установившейся скорости падения
как мы вскоре убедимся, есть функция скорости падения. Стало быть, полученное выражение для силы сопротивления представляет собой уравнение для определения установившейся скорости падения 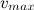 . Ясно, что при наличии среды энергия тела частично расходуется на преодоление ее сопротивления.
. Ясно, что при наличии среды энергия тела частично расходуется на преодоление ее сопротивления.
Число Рейнольдса. Разумеется, уравнения движения тела в жидкости невозможно даже начать решать, пока нам ничего неизвестно о модуле 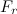 силы сопротивления. Величина этой силы существенно зависит от характера обтекания тела встречным потоком газа (или жидкости). При малых скоростях этот поток является ламинарным (то есть слоистым). Его можно представить себе как относительное движение не смешивающихся между собой слоев среды.
силы сопротивления. Величина этой силы существенно зависит от характера обтекания тела встречным потоком газа (или жидкости). При малых скоростях этот поток является ламинарным (то есть слоистым). Его можно представить себе как относительное движение не смешивающихся между собой слоев среды.
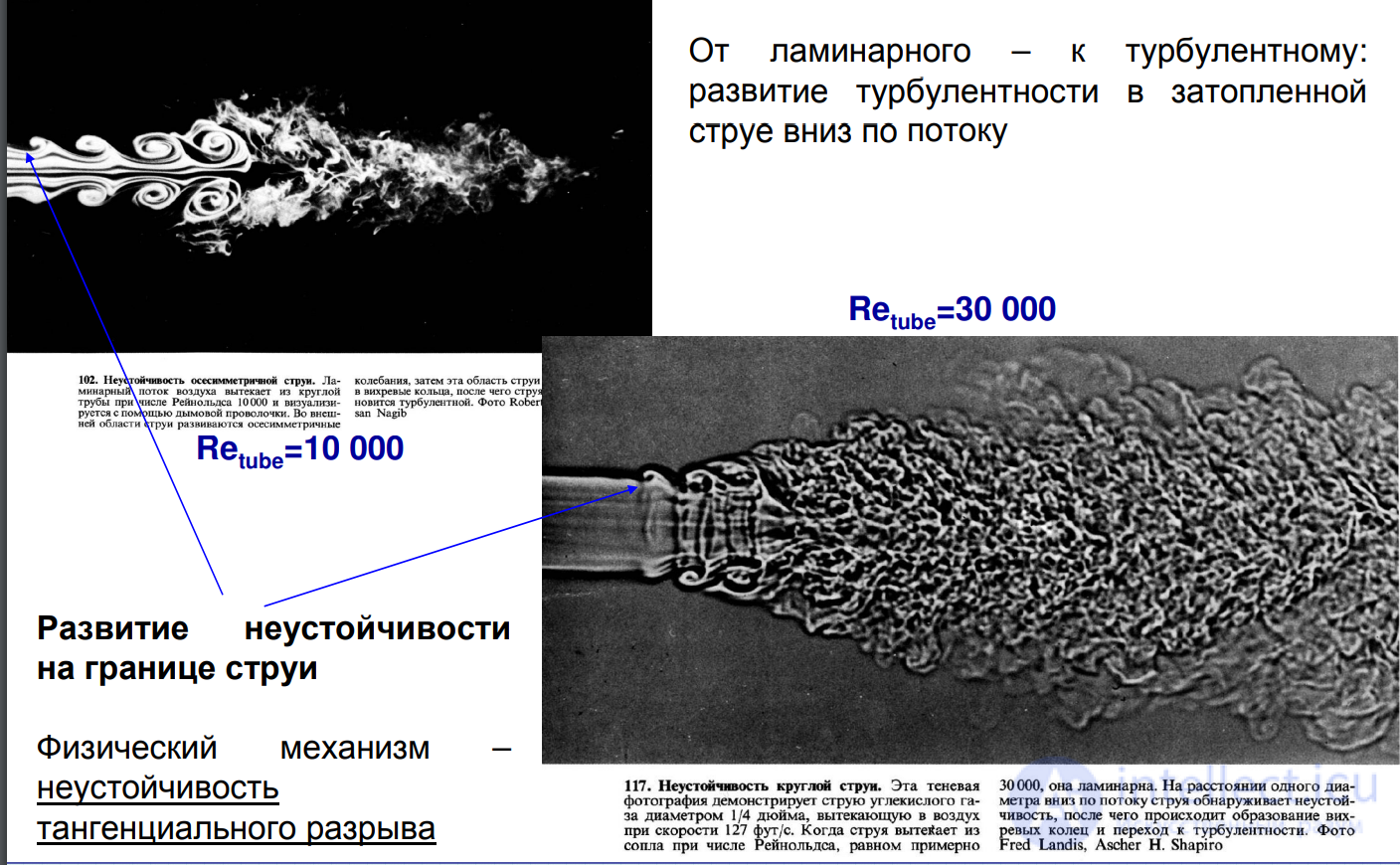
Ламинарное течение жидкости демонстрируется на опыте, показанном на рис. 13.
Как уже отмечалось в главе 9.3, при относительном движении слоев жидкости или газа между этими слоями возникают силы сопротивления движению, которые называются силами внутреннего трения. Эти силы обусловлены особым свойством текучих тел — вязкостью, которая характеризуется численно коэффициентом вязкости  . Приведем характерные значения
. Приведем характерные значения  для различных веществ: для воздуха (
для различных веществ: для воздуха ( = 1,8·10-5 Па·с), воды (
= 1,8·10-5 Па·с), воды ( = 10–3 Па·с), глицерина (
= 10–3 Па·с), глицерина ( = 0,85 Па·с). Эквивалентное обозначение единиц, в которых измеряется коэффициент вязкости: Па·с=кг·м–1·с–1.
= 0,85 Па·с). Эквивалентное обозначение единиц, в которых измеряется коэффициент вязкости: Па·с=кг·м–1·с–1.
Между движущимся телом и средой всегда существуют силы сцепления, так что непосредственно вблизи поверхности тела слой газа (жидкости) полностью задерживается, как бы «прилипая» к нему. Он трется о следующий слой, который слегка отстает от тела. Тот, в свою очередь, испытывает силу трения со стороны еще более удаленного слоя и т.д. Совсем далекие от тела слои можно считать покоящимися. Теоретический расчет внутреннего трения для движения шарика диаметром D приводит к формуле Стокса:
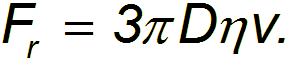
Подставляя формулу Стокса в выражение для силы сопротивления при установившемся движении, находим выражение для установившейся скорости падения шарика в среде:
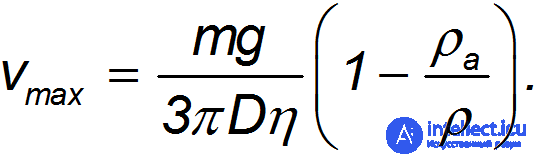
Видно, что чем легче тело, тем меньше скорость его падения в атмосфере. Полученное уравнение объясняет нам, почему пушинка падает медленнее,чем стальной шарик.
При решении реальных задач, например, вычислении установившейся скорости падения парашютиста при затяжном прыжке, не следует забывать, что сила трения пропорциональна скорости тела лишь для относительно медленного ламинарного встречного потока воздуха. При увеличении скорости тела вокруг него возникают воздушные вихри, слои перемешиваются, движение в какой-то момент становится турбулентным, и сила сопротивления резко возрастает. Внутреннее трение (вязкость) перестает играть сколько бы то ни было заметную роль.

Рис. 9.15 Фотография струи жидкости при переходе от ламинарного течения к турбулентному (число Рейнольдса Re=250)
Возникновение силы сопротивления можно тогда представить себе следующим образом. Пусть тело прошло в среде путь 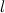 . При силе сопротивления
. При силе сопротивления 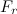 на это затрачивается работа
на это затрачивается работа

Если площадь поперечного сечения тела равна 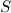 , то тело «натолкнется» на частицы, занимающие объем
, то тело «натолкнется» на частицы, занимающие объем 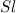 . Полная масса частиц в этом объеме равна
. Полная масса частиц в этом объеме равна  ·
·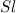 Представим, что эти частицы полностью увлекаются телом, приобретая скорость
Представим, что эти частицы полностью увлекаются телом, приобретая скорость  . Тогда их кинетическая энергия становится равной
. Тогда их кинетическая энергия становится равной

Эта энергия не появилась ниоткуда: она создана за счет работы внешних сил по преодолению силы сопротивления. Стало быть, A=К, откуда
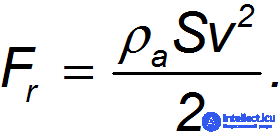
Мы видим, что теперь сила сопротивления сильнее зависит от скорости движения, становясь пропорциональной ее второй степени (ср. с формулой Стокса). В отличие от сил внутреннего трения ее часто называют силой динамического лобового сопротивления.
Однако предположение о полном увлечении частиц среды движущимся телом оказывается слишком сильным. В реальности любое тело так или иначе обтекается потоком, что уменьшает силу сопротивления. Принято использовать так называемый коэффициент сопротивления C, записывая силу лобового сопротивления в виде:

При турбулентном потоке в некотором интервале скоростей C не зависит от скорости движения тела, но зависит от его формы: скажем, для диска он равен единице, а для шара примерно 0,5.
Подставляя формулу для силы лобового сопротивления в выражение для силы сопротивления при установившемся движении, приходим к иному, нежели ранее полученная формула, выражению для установившейся скорости падения шара (при C = 0,5):

Применяя найденную формулу к движению парашютиста весом 100 кг с поперечным размером парашюта 10 м, находим
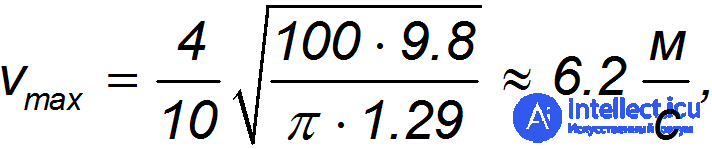
что соответствует скорости приземления при прыжке без парашюта с высоты 2 м. Видно, что для описания движения парашютиста больше подходит формула, соответствующая турбулентному потоку воздуха.
Выражение для силы сопротивления с коэффициентом сопротивления удобно использовать во всем интервале скоростей. Поскольку при малых скоростях режим сопротивления меняется, то коэффициент сопротивления в области ламинарного течения и в переходной области к турбулентному течению будет зависеть от скорости тела. Однако прямая зависимость C от  невозможна, поскольку коэффициент сопротивления безразмерен. Значит, он может быть лишь функцией какой-то безразмерной комбинации с участием скорости. Такая комбинация, играющая важную роль в гидро- и аэродинамике, называется числом Рейнольдса
невозможна, поскольку коэффициент сопротивления безразмерен. Значит, он может быть лишь функцией какой-то безразмерной комбинации с участием скорости. Такая комбинация, играющая важную роль в гидро- и аэродинамике, называется числом Рейнольдса  (см. тему 1.3).
(см. тему 1.3).
Число Рейнольдса — это параметр, описывающий смену режима при переходе от ламинарного течения к турбулентному. Таким параметром может служить отношение силы лобового сопротивления к силе внутреннего трения. Подставляя в формулу для силы сопротивления выражение для площади поперечного сечения шара 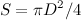 , убеждаемся, что величина силы лобового сопротивления с точностью до несущественных сейчас числовых факторов определяется выражением
, убеждаемся, что величина силы лобового сопротивления с точностью до несущественных сейчас числовых факторов определяется выражением

а величина силы внутреннего трения — выражением

Отношение этих двух выражений и есть число Рейнольдса:

Если речь идет не о движении шара, то под D понимается характерный размер системы (скажем, диаметр трубы в задаче о течении жидкости). По самому смыслу числа Рейнольдса ясно, что при его малых значениях доминируют силы внутреннего трения: вязкость велика и мы имеем дело с ламинарным потоком. При больших значениях числа Рейнольдса, наоборот, доминируют силы динамического лобового сопротивления и поток становится турбулентным.
Число Рейнольдса имеет огромное значение при моделировании реальных процессов в меньших (лабораторных) масштабах. Если для двух течений разных размеров числа Рейнольдса одинаковы, то такие течения подобны, и возникающие в них явления могут быть получены одно из другого простым изменением масштаба измерения координат и скоростей. Поэтому, например, на модели самолета или автомобиля в аэродинамической трубе можно предугадать и изучить процессы, которые возникнут в процессе реальной эксплуатации.
Коэффициент сопротивления. Итак, коэффициент сопротивления в формуле для силы сопротивления зависит от числа Рейнольдса:
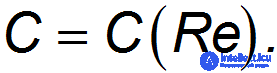
Эта зависимость имеет сложный характер, показанный (для шара) на рис. 9.16. Теоретически получить эту кривую трудно, и обычно используют зависимости, экспериментально измеренные для данного тела. Однако возможна качественная ее интерпретация.
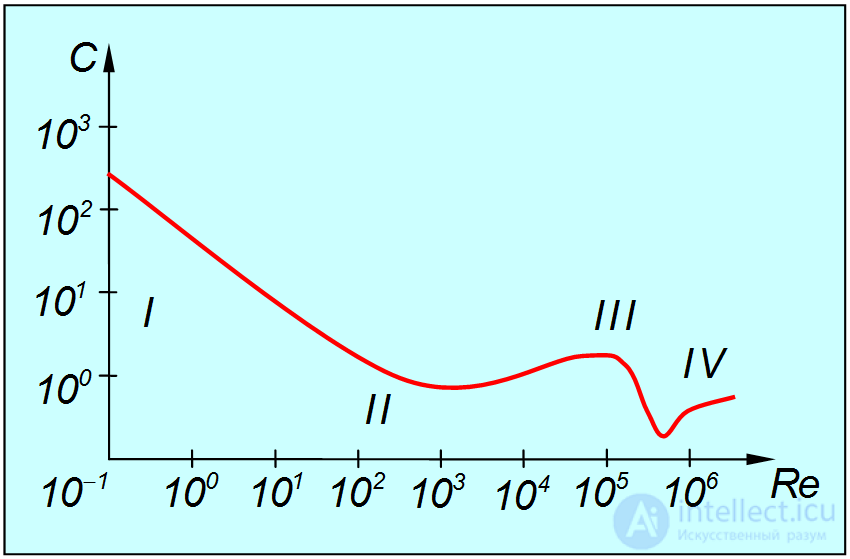
Рис. 9.16. Зависимость коэффициента сопротивления от числа Рейнолъдса (римскими цифрами показаны области значений Re; которым соответствуют различные режимы течения воздушного потока)
Область I. Здесь число Рейнольдса очень мало ( < 1) и течение потока ламинарно. Экспериментальная кривая описывается в этой области функцией
< 1) и течение потока ламинарно. Экспериментальная кривая описывается в этой области функцией
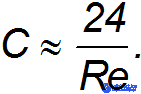
При подстановке этого значения в найденную ранее формулу для силы сопротивления и использовании 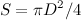 и выражения для числа Рейнольдса мы приходим к формуле Стокса. В этой области, как уже говорилось, сопротивление возникает вследствие вязкости среды.
и выражения для числа Рейнольдса мы приходим к формуле Стокса. В этой области, как уже говорилось, сопротивление возникает вследствие вязкости среды.
Область II. Здесь число Рейнольдса лежит в интервале 1 <  < 2·104. Данная область соответствует переходу от ламинарного к турбулентному течению. Экспериментальные данные свидетельствуют, что при увеличении числа Рейнольдса достигается некоторое его критическое значение, после которого стационарное ламинарное течение становится неустойчивым. Разумеется, это критическое значение не универсально и различается для разных типов течений. Но его характерная величина порядка нескольких десятков.
< 2·104. Данная область соответствует переходу от ламинарного к турбулентному течению. Экспериментальные данные свидетельствуют, что при увеличении числа Рейнольдса достигается некоторое его критическое значение, после которого стационарное ламинарное течение становится неустойчивым. Разумеется, это критическое значение не универсально и различается для разных типов течений. Но его характерная величина порядка нескольких десятков.
При  лишь слегка больших критического значения появляется нестационарное периодическое движение потока, характеризуемое некоторой частотой. При дальнейшем увеличении
лишь слегка больших критического значения появляется нестационарное периодическое движение потока, характеризуемое некоторой частотой. При дальнейшем увеличении  периодическое движение усложняется, и в нем появляются новые и новые частоты. Этим частотам соответствуют периодические движения (вихри), пространственные масштабы которых становятся все более мелкими. Движение приобретает более сложный и запутанный характер — развивается
турбулентность . В данной области коэффициент сопротивления продолжает падать с ростом
периодическое движение усложняется, и в нем появляются новые и новые частоты. Этим частотам соответствуют периодические движения (вихри), пространственные масштабы которых становятся все более мелкими. Движение приобретает более сложный и запутанный характер — развивается
турбулентность . В данной области коэффициент сопротивления продолжает падать с ростом  , но медленнее. Минимум достигается при
, но медленнее. Минимум достигается при  = (4–5)·103, вслед за чем С несколько повышается.
= (4–5)·103, вслед за чем С несколько повышается.
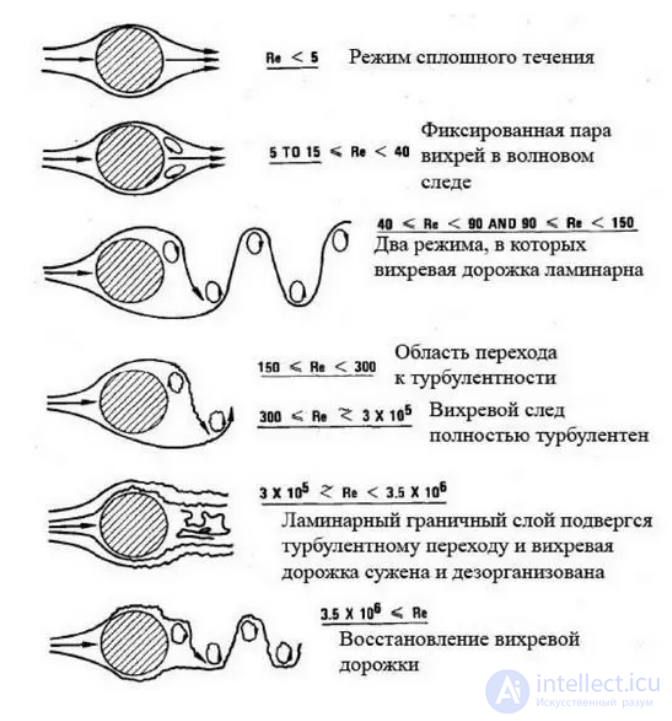
Область III. Эта область соответствует развитому турбулентному течению потока вокруг шара, а с этим режимом мы уже встречались выше. Характерные здесь значения числа Рейнольдса лежат в интервале 2·104 <  < 2·105.
< 2·105.
При движении тело оставляет за собой турбулентный след, за пределами которого течение ламинарно. Вихревой турбулентный след легко наблюдать, например, за кормой корабля. Часть поверхности тела непосредственно примыкает к области турбулентного следа, а его передняя часть — к области ламинарного течения. Граница между ними на поверхности тела называется линией отрыва. Физической причиной возникновения силы сопротивления является разность давлений на передней и задней поверхностях тела. Оказывается, что положение линии отрыва определяется свойствами пограничного слоя и не зависит от числа Рейнольдса. Поэтому коэффициент сопротивления примерно постоянен в этом режиме.
Область IV. Однако такой режим обтекания тела не может поддерживаться до сколь угодно больших значений  . В какой-то момент передний ламинарный пограничный слой турбулизируется, что отодвигает назад линию отрыва. Турбулентный след за телом сужается, что приводит к резкому (в 4–5 раз) падению сопротивления среды. Это явление, названное кризисом сопротивления, происходит в узком интервале значений
. В какой-то момент передний ламинарный пограничный слой турбулизируется, что отодвигает назад линию отрыва. Турбулентный след за телом сужается, что приводит к резкому (в 4–5 раз) падению сопротивления среды. Это явление, названное кризисом сопротивления, происходит в узком интервале значений  = (2–2,5)·105. Строго говоря, приведенные теоретические соображения могут измениться при учете сжимаемости среды (воздуха, в нашем случае). Однако это проявится, как мы уже обсуждали, при скоростях объектов, сравнимых со скоростью звука.
= (2–2,5)·105. Строго говоря, приведенные теоретические соображения могут измениться при учете сжимаемости среды (воздуха, в нашем случае). Однако это проявится, как мы уже обсуждали, при скоростях объектов, сравнимых со скоростью звука.


порождение турбулентности решеткой
подходы для моделирования турбулентности
При развитой турбулентности: λ << lT<< L – инерционный интервал широкий, и в нем
"помещаются" все модели турбулентности:
- RANS: масштаб сечения потока ~L: масштаб "закачки" энергии в поток;
- LES: до масштаба lT: lT<< L (желательно); при развитой турбулентности lT>> λ;
- DNS: до микромасштаба λ – все неоднородности потока

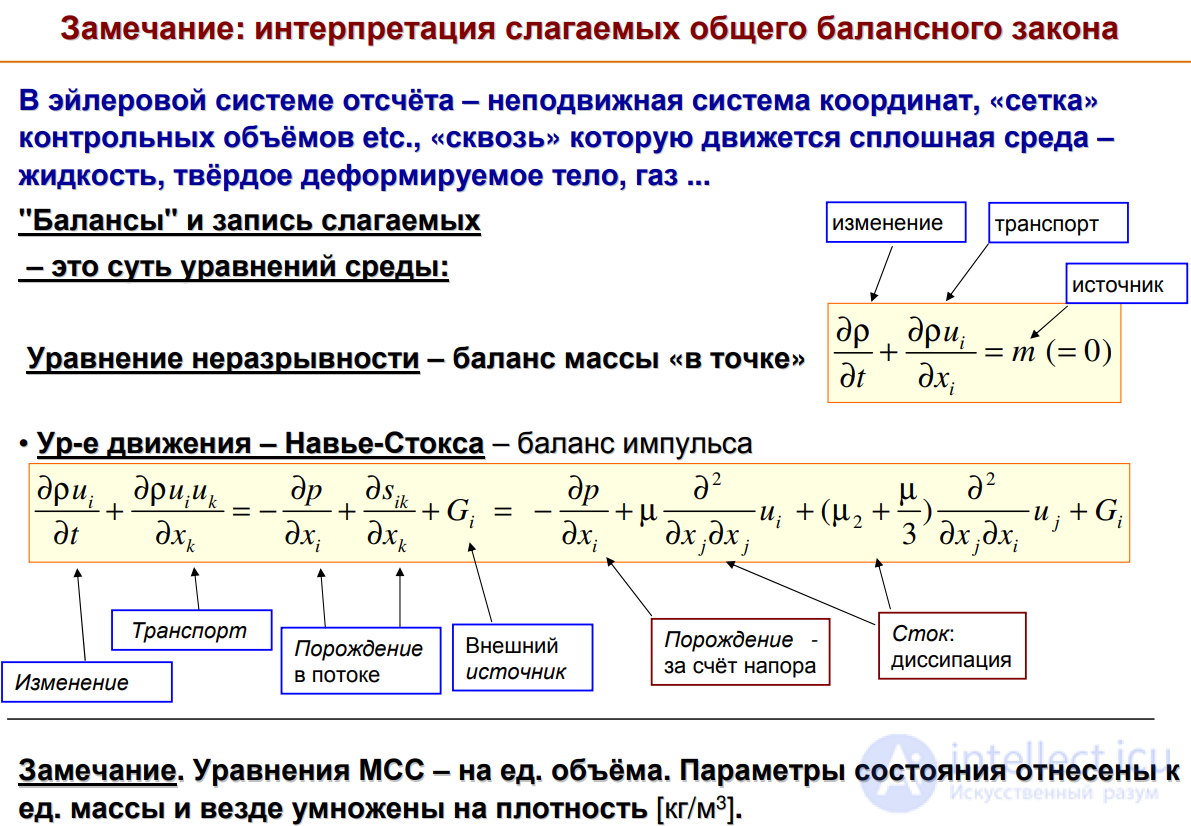
Уравнение Навье-Стокса описывает всю гидродинамику ньютоновской жидкости, включая детали турбулентного течения;
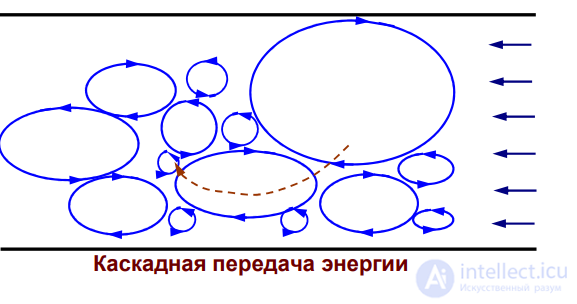
Каскадная передача энергии используемая для модлирования турбулентности
RANS модели, основанные на уравнении для турбулентной кинетической энергии (ТКЭ)
0. ТКЭ и ее диссипация: они существуют и важны для описания
1. Уравнение для ТКЭ – вывод уравнения:〈уравнение для К〉 – уравнение для 〈К〉 = уравнение для 〈k 〉
2. Уравнения для диссипации ТКЭ – ввод уравнения ...
3. Двухпараметрические модели турбулентности k-ε и k-ω

Исследование, описанное в статье про механика жидкостей и газов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое механика жидкостей и газов, закон паскаля (гидростатики), уравнение непрерывности, движение тел в среде с сопротивлением, турбулентность, ламинарность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики