4.5 Кинетическая энергия, понятие и виды кратко

Сразу хочу сказать, что здесь никакой воды про кинетическая энергия, и только нужная информация. Для того чтобы лучше понимать что такое кинетическая энергия , настоятельно рекомендую прочитать все из категории Физические основы механики.

кинетическая энергия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек . Работа всех сил, действующих на материальную точку при ее перемещении, идет на приращение кинетической энергии . Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

,

где индекс нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения . Более строго, кинетическая энергия есть разность между полной энергией системы и ее энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением . Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: , , и другие. В системе СИ она измеряется в джоулях (Дж).

Рассмотрим случай, когда материальная точка движется из точки 1 в точку 2 под действием приложенных к ней сил (рис.4.4.)

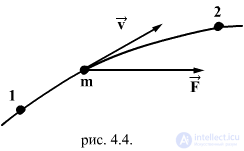
Причем силы, действующие на материальную точку, могут иметь разную природу, т.е. могут быть консервативными и неконсервативными. Уравнение движения в этом случае запишется в виде

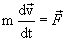(4.6)

где
Перепишем (4.6) в виде

(4.7)

Умножим скалярно уравнение (4.7) на 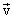и проинтегрируем от точки1 до точки 2, получим:

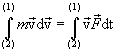(4.8)

Учитываем то, что 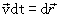, и интеграл в правой части выражения (4.8) представляет собой работу всех сил, на участке 1-2, можно записать:

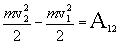(4.9)

величина

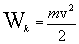(4.10)

называется кинетической энергией материальной точки. Таким образом, кинетическая энергия материальной точки – это энергия, которой обладает эта точка вследствие своего движения.

Из полученного выражения (4.9) следует, что работа всех сил, действующих на материальную точку на участке траектории 1-2 равна изменению ее кинетической энергии на этом участке.

История понятия

Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.), посвященных понятию «живой силы» .

Кинетическая энергия в классической механике

Случай одной материальной точки

По определению, кинетической энергией материальной точки массой называется величина

,

при этом предполагается, что скорость точки всегда значительно меньше скорости света. С использованием понятия импульса () данное выражение примет вид .

Если — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как . Скалярно умножив его на перемещение материальной точки и учитывая, что , причем , получим .

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина остается постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твердого тела

При рассмотрении движения абсолютно твердого тела его можно представить как совокупность материальных точек. Об этом говорит сайт https://intellect.icu . Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кенига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

Здесь — масса тела, — скорость центра масс, и — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс .

Кинетическая энергия в гидродинамике

В гидродинамике вместо массы материальной точки рассматривают массу единицы объема, то есть плотность жидкости или газа . Тогда кинетическая энергия, приходящаяся на единицу объема, двигающегося со скоростью , то есть плотность кинетической энергии (Дж/м³), запишется:

где по повторяющемуся индексу , означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осредненные величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путем осреднения уравнений Навье-Стокса . Если, в согласии с методом Рейнольдса, представить , , где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретет вид:

где — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности» , часто называемой просто «энергией турбулентности»), а — плотность кинетической энергии, связанная с турбулентным потоком вещества ( — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения зависит от выбора системы координат, в то время как кинетическая энергия турбулентности от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объему или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определенную погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

Кинетическая энергия в квантовой механике

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (, — мнимая единица):

где — редуцированная постоянная Планка, — оператор набла, — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шредингера .

Кинетическая энергия в релятивистской механике

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как:

где — масса покоя,

— скорость движения в выбранной инерциальной системе отсчета,

— скорость света в вакууме ( — энергия покоя).

Или выражение для кинетической энергии в виде ряда Маклорена:

При скоростях много меньших скорости света () пренебрегаем членами разложения с высшими степенями и выражение для переходит в классическую формулу .

Как и в классическом случае, имеет место соотношение , получаемое посредством умножения на выражения второго закона Ньютона (в виде ).

Свойства кинетической энергии

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему
• Инвариантность по отношению к повороту системы отсчета. Кинетическая энергия не зависит от положения точки, направления ее скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата ее скорости
• Неинвариантность по отношению к смене системы отсчета в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчета к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея . Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии

Физический смысл кинетической энергии

Работа всех сил, действующих на материальную точку при ее перемещении, идет на приращение кинетической энергии :

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твердое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

Пример задачи

На какой высоте кинетическая энергия мяча будет равна потенциальной, если он брошен вертикально вверх с начальной скоростью 19,6 м/с?

Вау!! 😲 Ты еще не читал? Это зря!

• Теорема о кинетической энергии системы
• Потенциальная энергия
• Закон сохранения энергии
• Хаос
• Энтальпия
• Негэнтропия
• Термодинамика
• парадокс кинетической энергии , взрыв металла при ударе ,
• Теорема Кенига

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про кинетическая энергия Надеюсь, что теперь ты понял что такое кинетическая энергия и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики

Из статьи мы узнали кратко, но содержательно про кинетическая энергия