Лекция
Привет, Вы узнаете о том , что такое математика в физике, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое математика в физике , настоятельно рекомендую прочитать все из категории Физические основы механики.
Предметом естествознания в широком смысле является познание окружающего нас мира. Задача естественных наук состоит в том, чтобы сформировать в нашем сознании такую модель физического мира, которая наиболее полно отражала бы его свойства и обеспечивала бы такие соотношения между элементами модели, какие существуют между элементами внешнего мира. Дж. Максвелл писал «Точные науки стремятся к тому, чтобы свести загадки природы к определению некоторых величин путем операций над числами». Поэтому естественные науки «говорят» с природой на языке математики. Принцип «nulla scientia potest sciri sine mathematika» (никакую науку нельзя познать без математики) был сформулирован еще в средневековье. Но откуда взять эти самые числа, которыми оперирует математика, которые должны фигурировать в уравнениях, выражающих те или иные закономерности природы? Единственным источником их может служить сама природа (варианты «божественных» откровений мы не рассматриваем как малопрактичные).
Есть у меня шестерка слуг, проворных, удалых.
И все, что вижу я вокруг, - все знаю я от них.
Они по знаку моему являются в нужде.
Зовут их Как и Почему, Кто, Что, Когда и Где.
Р. Киплинг
Естествознание — это комплекс экспериментальных наук, в основе которых лежат наиболее общие закономерности, изучаемые физикой.
Естественные науки начинаются с наблюдений и измерений, ими же проверяются и питаются в своем развитии. Конечно, новые идеи в науке появляются и благодаря умозрительным рассуждениям. Но окончательный ответ на решающие вопросы может быть получен только в эксперименте. Да и сами эти идеи на пустом месте не возникают.
С помощью приборов мы задаем природе вопросы, и получаем ответы, которые «обрабатываем» в нашем мозгу, на своих компьютерах. Понять явление — значит уметь его описать, знать условия, при которых оно происходит, предсказать его последствия. Важно лишь правильно сформулировать свои вопросы, и тогда мы получаем шанс, что природа на них ответит.
Природа (и вместе с ней наука) не отвечает на вопрос «почему?». Почему тело под действием силы приобретает ускорение? Почему электрическое поле действует на заряд? Разве кто-нибудь в состоянии ответить на эти вопросы? Мы можем лишь констатировать факты такого типа:
Иными словами, наука в принципе может ответить лишь на вопрос «как?». Как устроен наш мир, какие законы им управляют, каков механизм тех или иных процессов, каковы их характерные времена и масштабы, какими уравнениями они описываются.
Физика изучает самые фундаментальные закономерности природы, самые простые ее составные части. Благодаря этой «простоте» физика (так же, как и химия, молекулярная биология и т. п.) имеет дело с воспроизводимыми ситуациями. Это означает, что мы можем повторить наши эксперименты, и если все условия в точности выполнены, то и результаты будут такими же. Подобное вряд ли возможно, например, в геологии, не говоря уже об общественных науках (экономике, истории и т.д.). Важно понимать также, что физический эксперимент никогда не бывает идеальным, любое измерение производится с определенной точностью. И когда мы говорим о том или ином законе природы, мы должны помнить, что этот закон был установлен в каких-то конкретных условиях и имеет, как правило, конкретные пределы применимости.
Физические модели и теории предназначены для приведения в соответствие между собой тех сведений, которые мы получаем, исследуя явления природы. Ни одна из теорий не может претендовать на звание истинной, она лишь дает наилучшее для данного времени описание той области, в которой она применяется. Мы называем теорию «хорошей», если она:
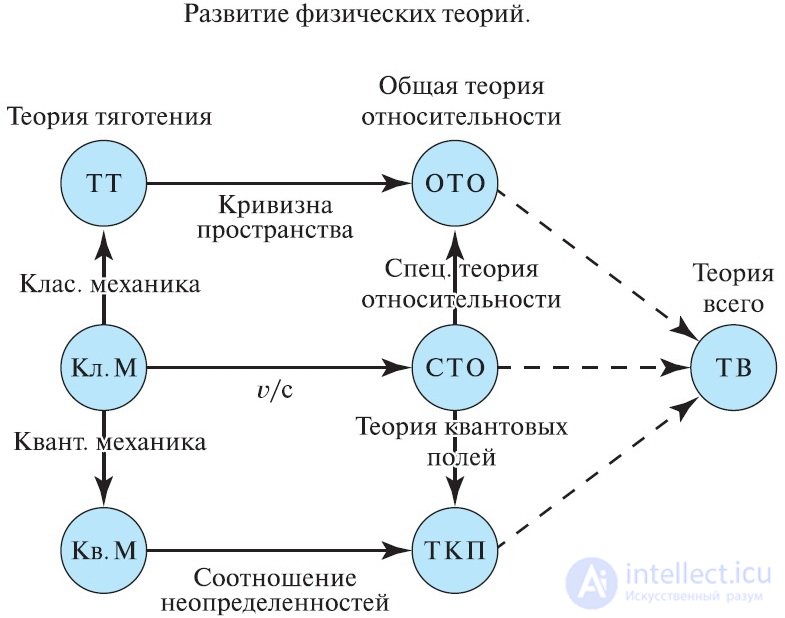
Рис. 1.1. Развитие физических теорий
История науки показала, что, как правило, «хорошая» теория допускает возможность усовершенствования. Это не значит, что хорошая» теория верна безусловно. Теория всегда может быть изменена (или же полностью отвергнута), если станут известны новые факты. Просто при более глубоком проникновении в суть вещей оказывается, что «хорошая» теория является частью более общей теории и имеет свою область применимости. Так случилось, скажем, с механикой Ньютона после открытия теории относительности.
Ограничения классической механики
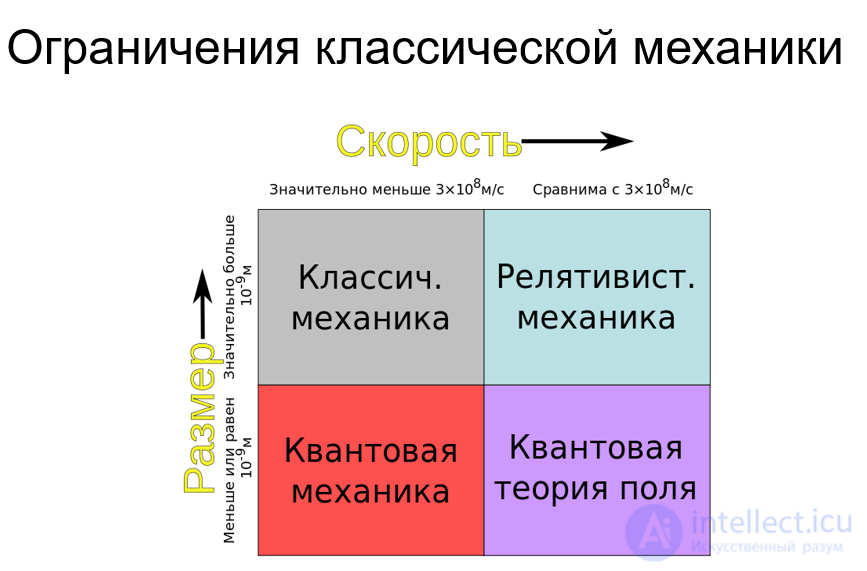
Результаты многочисленных опытных наблюдений обобщают в виде физических законов, которые представляют собой некоторые утверждения относительно связей между теми или иными физическими величинами. Для проверки на опыте этих утверждений необходимо независимыми способами измерить все те величины, которые связаны в данном физическом законе. Измерение любой физической величины проводится путем ее сравнения с определенным стандартным значением,принятым за единицу этой величины.Эти единицы обязательно должны указываться вместе с численным значением результата. Метрическая система мер, созданная в эпоху Великой французской революции, по мысли ее авторов должна была служить «на все времена, для всех народов, для всех стран».
Основные единицы измерения выбираются произвольно.
Поясним факт произвольности выбора основных единиц следующими примерами. Длину можно с одинаковым успехом измерять в аршинах, саженях, футах, ярдах, метрах и так далее. Расстояние от Москвы до Петербурга по железной дороге составляет 650 километров (км), это же расстояние в морских милях (1 международная морская миля равна 1852 метрам) равно примерно 351 морской миле. Массу можно измерять в килограммах или, например, в фунтах. Можно указать: фунт британский торговый — 453,592 грамма (г), фунт тройский или аптекарский — 373,242 г, русский фунт, употреблявшийся до введения метрической системы — 409,512 г.

Рис. 1.2. Масса в природе и технике
Для тех, кто внимательно следит за международной торговлей золотом, укажем, что на этих торгах, по традиции, указывается стоимость тройской унции золота, то есть 31,1034768 грамма (1/12 аптекарского фунта).
Цель указанных примеров состоит в том, чтобы показать, что свобода (произвольность) выбора основных единиц измерения способна привести к весьма дорогостоящей путанице. В действительности свобода выбора основных единиц, претендующих на то, чтобы, как сказано выше, служить «на все времена, для всех народов, для всех стран», ограничена целым рядом жестких требований. А именно (цитируем по книге А.Г. Чертова "Международная система единиц измерения", Москва, Росвузиздат, 1963):
1."Число основных единиц системы необходимо свести к разумному минимуму. С увеличением числа основных единиц системы увеличивается и число размерных коэффициентов в физических формулах, что создает неудобство при использовании системы.
Наоборот, в системе с меньшим числом основных единиц уменьшается число размерных коэффициентов. Однако с уменьшением числа основных единиц системы увеличивается число производных единиц с одинаковой размерностью, что также создает неудобство при пользовании системой единиц.
Опыт показывает, что наиболее удачной системой единиц для измерения механических величин оказалась система с тремя основными единицами: единицами длины, массы и времени или длины, силы и времени. Для измерения величин молекулярной физики наиболее удобной является система с четырьмя основными единицами: единицами длины, массы, времени и температуры. Для измерения электромагнитных величин применяются системы также с четырьмя основными единицами.
2.Нужен рациональный выбор основных единиц. Необходимо, чтобы как сами основные единицы, так и полученные на их основе производные единицы по своему размеру были удобны для практических целей. Кроме того, основные единицы должны быть такими, чтобы их можно было воспроизвести в виде эталонов или эталонными установками с точностью, удовлетворяющей требованиям науки и техники.
3.Система должна быть когерентной, т. е. чтобы во всех определяющих уравнениях коэффициент пропорциональности являлся безразмерной величиной, равной единице.
4.Система должна содержать единицы измерения всех величин, входящих в те разделы физики, для которых система предназначена.
5.Система должна содержать только одну единицу измерения для каждой физической величины.
6.Система единиц, предназначенная для определенного раздела физики, должна являться основанием для построения систем единиц других разделов физики или быть их логическим развитием.
Например, система механических единиц МКС является основанием для построения системы электромагнитных единиц МКСА. В свою очередь система МКСА является результатом логического распространения системы МКС на область электромагнитных явлений.
Наличие такой логической связи между отдельными системами, действующими в различных разделах физики, позволяет создать единую систему, охватывающую широкий круг областей физической науки".
В последнее десятилетие (1950–1960 годы) была проделана большая работа международными организациями по созданию такой системы. Эта система основывается на шести основных единицах и получила название Международной системы единиц (SI) — начальные буквы французского наименования Systeme International.
Международная система единиц (SI, по-русски СИ) была принята XI Генеральной конференцией по мерам и весам, с 1 января 1963 года она введена в СССР в качестве Государственного стандарта.
Основной особенностью современных единиц является то, что между единицами разных величин устанавливаются зависимости на основе тех или иных законов или определений, которыми связаны между собой измеряемые величины. Таким образом, из нескольких условно выбираемых основных единиц строятся производные единицы.
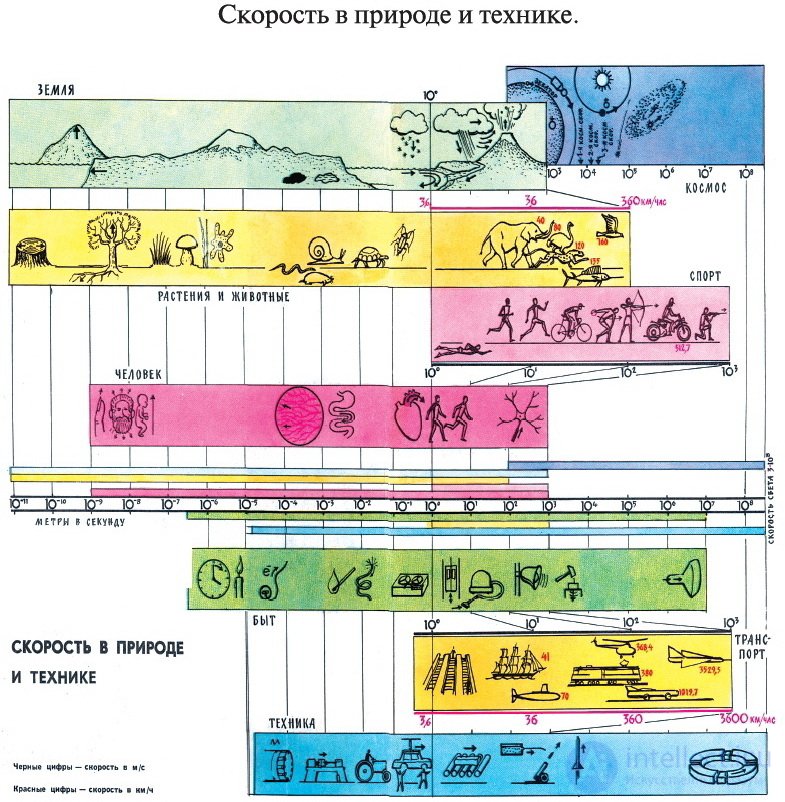
Рис. 1.3. Скорость в природе и технике
Единицы, которые выводятся из основных и дополнительных с помощью физических законов и определений, называются производными единицами.
Совокупность основных, дополнительных и производных единиц измерения называется системой единиц измерения.
В зависимости от выбора основных и дополнительных единиц измерения могут быть построены различные системы единиц измерения, отличающиеся практической целесообразностью и удобством пользования.

Рис. 1.4. Плотность вещества в природе
Отметим, что в физике вообще и в теоретической физике в особенности широко используются системы так называемых натуральных единиц. Подробно речь о таких системах единиц пойдет в тех разделах, где их использование общепринято, здесь же приведем один пример для краткого пояснения того, что имеется ввиду.
Атомная система единиц вводится из следующих соображений. В атоме (молекуле) главным действующим лицом является электрон, Это связано с тем, что ядра в несколько тысяч раз тяжелее электронов и, как правило, могут считаться неподвижными. Действительно, отношение массы самого легкого ядра — протона к массе электрона равно 1836. Главным взаимодействием, определяющим свойства атома, является электромагнитное, прежде всего электростатическое — кулоновское. Наконец, атом — квантовый объект: классическая (не квантовая) теория его свойства не описывает. В этих условиях естественно предположить (так оно и есть), что масштабы "атомного мира" определяются такими фундаментальными мировыми постоянными как: 1) масса электрона  ; 2) элементарный заряд — модуль заряда электрона, он же заряд протона
; 2) элементарный заряд — модуль заряда электрона, он же заряд протона  ; 3) квантовая постоянная — постоянная Планка
; 3) квантовая постоянная — постоянная Планка 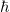 . Другими словами, естественно положить
. Другими словами, естественно положить 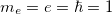 , что означает лишь следующее: массы всех объектов будем измерять в массах электрона, все заряды — в зарядах протона, а все величины с размерностью момента импульса или произведения энергии на время — в постоянных Планка. В этих единицах масса протона равна 1836, а заряд ядра равен числу протонов в ядре, то есть атомному номеру соответствующего элемента. К примеру, единица длины равна радиусу первой боровской орбиты электрона в атоме водорода
, что означает лишь следующее: массы всех объектов будем измерять в массах электрона, все заряды — в зарядах протона, а все величины с размерностью момента импульса или произведения энергии на время — в постоянных Планка. В этих единицах масса протона равна 1836, а заряд ядра равен числу протонов в ядре, то есть атомному номеру соответствующего элемента. К примеру, единица длины равна радиусу первой боровской орбиты электрона в атоме водорода 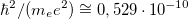 метра; единица скорости равна
метра; единица скорости равна  метра в секунду (c — скорость света в вакууме), а единица энергии равна
метра в секунду (c — скорость света в вакууме), а единица энергии равна  Дж. Столь крупная единица скорости — больше двух тысяч километров в секунду и столь малые единицы длины и энергии безусловно крайне неудобны в технике (см. ниже систему СИ) и, тем более, в быту, но очень удобны в мире атомов и молекул.
Дж. Столь крупная единица скорости — больше двух тысяч километров в секунду и столь малые единицы длины и энергии безусловно крайне неудобны в технике (см. ниже систему СИ) и, тем более, в быту, но очень удобны в мире атомов и молекул.
Такого рода системы единиц замечательны главным образом тем, что никак не связаны с параметрами человеческого организма (не антропогенные единицы) или другими «местными» — Земными масштабами. Под антропогенностью имеется ввиду следующее: секунда — примерно интервал времени между двумя последовательными «ударами» сердца спокойно лежащего здорового человека, метр — примерно расстояние от левого плеча до концов пальцев горизонтально вытянутой правой руки, сажень — расстояние между концами пальцев горизонтально вытянутых рук, килограмм — примерно масса двух кулаков взрослого мужчины. Связывать одну из единиц времени, а именно сутки, с периодом вращения Земли тоже не очень хорошо: во-первых, период вращения Земли меняется, а во-вторых, другие разумные существа могут и не знать периода обращения Земли вокруг своей оси, такая единица времени будет им совершенно непонятной.
В Международной системе единиц СИ (начальные буквы французского наименования Systeme International) в качестве основных выбраны следующие семь единиц:
Основные единицы измерения

В квадратных скобках указано общепринятое обозначение для размерностей: длину можно измерять в метрах, ярдах или попугаях, но обозначение L (от англ. length) всегда подскажет нам, что мы имеем дело с длиной. Аналогично вводится обозначение размерности времени Т (от англ. time).

Рис. 1.5. "Хронография" развития Вселенной
Кроме основных, в системе СИ используются дополнительные единицы.
Дополнительные единицы измерения
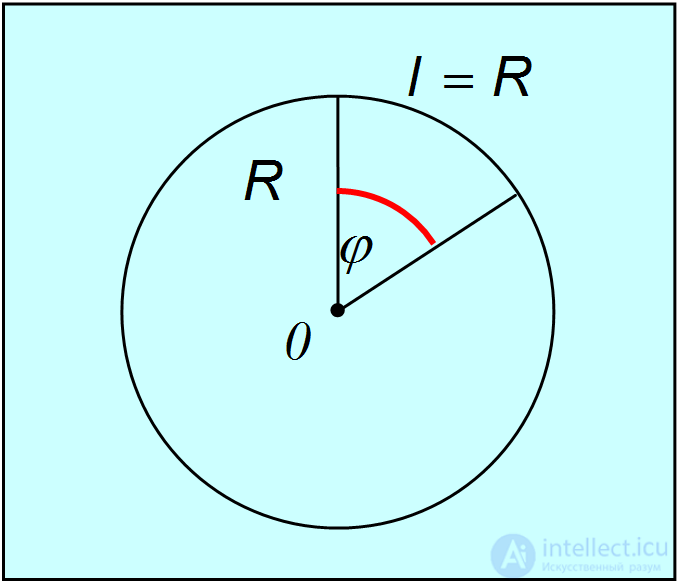
Рис. 1.6 Определение единицы плоского угла в СИ
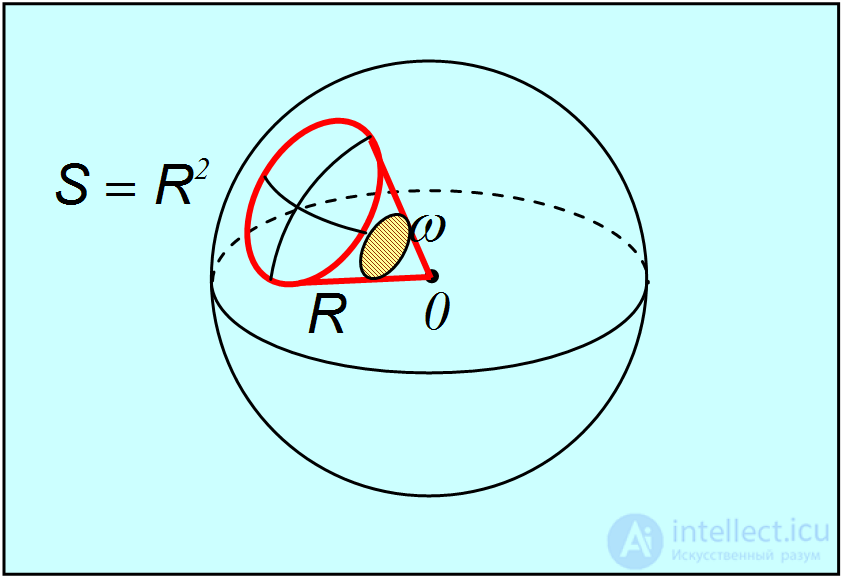
Рис. 1.7. Определение телесного угла
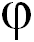 ], 1 рад (радиан). Радиан — это центральный угол, опирающийся на дугу, длина которой равна ее радиусу (рис. 1.6).
], 1 рад (радиан). Радиан — это центральный угол, опирающийся на дугу, длина которой равна ее радиусу (рис. 1.6). ], 1 ср (стерадиан). Телесный угол в 1 Стерадиан — это телесный угол, опирающийся на участок сферической поверхности произвольной формы, площадь которой равна квадрату ее радиуса (рис. 1.7).
], 1 ср (стерадиан). Телесный угол в 1 Стерадиан — это телесный угол, опирающийся на участок сферической поверхности произвольной формы, площадь которой равна квадрату ее радиуса (рис. 1.7).Для простоты ученые стремятся выбрать минимальное число основных величин, которое позволяет дать полное описание физического мира. В выборе основных величин и их производных имеется некоторый произвол. С двумя из этих единиц мы знакомимся уже с самого детства. Это естественно, так как все события происходят где-то и когда-то. Мы обитаем в пространстве, которое измеряем единицами длины. Мы живем во времени, и человечество научилось его измерять в глубокой древности. Почему наш мир существует во времени и в пространстве? Мы договорились таких вопросов не ставить, так как наука все равно на них не ответит. Но каковы свойства пространства и времени? — этот вопрос вполне закономерен. Изучая физические явления, мы узнаем свойства пространства и времени, и процесс этого познания еще не завершен.
До недавнего времени международным эталоном метра считалось расстояние между двумя штрихами на стержне из платинового сплава, хранящимся в Международном бюро мер и весов в Париже. В последние годы эталон метра определялся числом длин световой волны конкретной (оранжевой) спектральной линии изотопа криптона 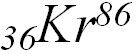 при переходе электрона между квантовыми состояниями
при переходе электрона между квантовыми состояниями 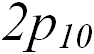 и
и 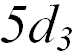 (что это такое, мы узнаем в заключительных частях курса). Метр содержит 1 650 763.73 длины волны этой спектральной линии в вакууме. Вследствие возросших требований к точности эталона длины в 1983 г. было принято следующее определение метра: это расстояние, проходимое светом в вакууме за время
(что это такое, мы узнаем в заключительных частях курса). Метр содержит 1 650 763.73 длины волны этой спектральной линии в вакууме. Вследствие возросших требований к точности эталона длины в 1983 г. было принято следующее определение метра: это расстояние, проходимое светом в вакууме за время  = 1/299 792 458 секунд. Иными словами, постулировано, что скорость света с в точности равна
= 1/299 792 458 секунд. Иными словами, постулировано, что скорость света с в точности равна  = 2.99792458 • 108 м/с. В сущности, это означает, что вместо длины в качестве фундаментальной единицы выбрана скорость, а длина стала производной единицей.
= 2.99792458 • 108 м/с. В сущности, это означает, что вместо длины в качестве фундаментальной единицы выбрана скорость, а длина стала производной единицей.
На рис. 1.8 представлены пространственные расстояния, характерные для окружающего мира.
Рис. 1.8. Пространственные масштабы в природе
Весь доступный нашим наблюдениям мир заключен в интервале от 1026 м (радиус видимой части Вселенной) до 10-18 м (расстояния, «прощупываемые» в современных экспериментах с элементарными частицами). Для удобства шкала расстояний  изображена в логарифмическом масштабе
изображена в логарифмическом масштабе 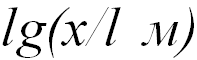 . Это значит, что расстоянию 10 м на шкале соответствует число 1, а расстоянию 100 км = 100 000 м — число 5.
. Это значит, что расстоянию 10 м на шкале соответствует число 1, а расстоянию 100 км = 100 000 м — число 5.
Если раньше время определяли по Солнцу, и секунда соответствовала 1/86 400 средних солнечных суток, то теперь она равна продолжительности 9 192 631 770 периодов колебаний световой волны, излученной при переходе между сверхтонкими уровнями основного состояния атома цезия  . Цезиевый стандарт очень точен: за 6 000 лет двое цезиевых часов могут разойтись лишь на одну секунду. Существуют и более точные часы на водородном мазере: разница в секунду набегает здесь за 30 млн. лет. Возможно, водородный мазер будет принят когда-нибудь в качестве нового эталона времени.
. Цезиевый стандарт очень точен: за 6 000 лет двое цезиевых часов могут разойтись лишь на одну секунду. Существуют и более точные часы на водородном мазере: разница в секунду набегает здесь за 30 млн. лет. Возможно, водородный мазер будет принят когда-нибудь в качестве нового эталона времени.
Некоторые временные интервалы, встречающиеся в природе, иллюстрирует рис. 1.9.
Рис. 1.9. Временные интервалы в природе
Самое большое время, о котором мы можем получить какие-то сведения — это время существования видимой части Вселенной. По современным представлениям она родилась в результате так называемого Большого Взрыва примерно 14 млрд. лет тому назад (6 • 1017 с). Наименьшие времена (10-26 с), с которыми мы сталкиваемся, по порядку величины соответствуют времени, за которое свет проходит самые малые расстояния, доступные сейчас для изучения.
Действительно понимающий природу
того или иного явления должен получить
основные законы из соображений размерности
Э. Об этом говорит сайт https://intellect.icu . Ферми
Физические величины бывают размерными и безразмерными.
Величина называется размерной, если ее численное значение зависит от выбора системы единиц.
Так, известный промежуток времени от восхода до восхода Солнца мы можем выразить как 1 сутки, или как 24 часа, или как 1 440 мин., или 86 400 с. Числа меняются, но мы говорим о том же самом интервале времени.
Величина называется безразмерной, если ее значение сохраняется неизменным при любом выборе системы единиц.
Например, высота Эвереста (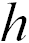 = 8 848 м) и радиус Земли (
= 8 848 м) и радиус Земли (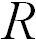 = 6 370 км) — размерные величины, но их отношение уже величина безразмерная: независимо от системы единиц
= 6 370 км) — размерные величины, но их отношение уже величина безразмерная: независимо от системы единиц
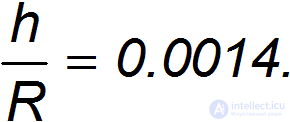
Некоторых пояснений требует такой объект как «угол». В математической энциклопедии (Москва, Советская энциклопедия, 1985, том 5, стр. 467) угол определен следующим образом: «Уугол — геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи называются сторонами угла, а их общее начало — вершиной угла». Эквивалентное определение: плоский угол — часть плоскости между двумя лучами, выходящими из одной точки. Радианная мера центрального угла вводится (см. рис. 1.7) как отношение длины дуги окружности, на которую он опирается к длине радиуса этой окружности: 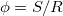 . Очевидно, что радианную меру можно ввести для любого угла, достаточно ножку циркуля поставить в вершину угла, провести окружность произвольного радиуса и вычислить отношение длины дуги, ограниченной сторонами угла, к радиусу этой дуги. Широко распространенное отождествление угла (как геометрической фигуры) и его радианной меры требует такого дополнительного разъяснения: угол величина безразмерная, равная «отношению длины дуги к радиусу», а единицы измерения этой безразмерной величины могут быть разными. Например, такой единице измерения угла как градус просто соответствует дуга длиной не в радиус, а в 1/360 часть длины окружности. Другой пример: в морской навигации для измерения углов используется «румб», этой единице измерения соответствует дуга длиной в 1/32 часть окружности. Понимание того факта, что угол — величина безразмерная, весьма важно при анализе размерностей (см. ниже).
. Очевидно, что радианную меру можно ввести для любого угла, достаточно ножку циркуля поставить в вершину угла, провести окружность произвольного радиуса и вычислить отношение длины дуги, ограниченной сторонами угла, к радиусу этой дуги. Широко распространенное отождествление угла (как геометрической фигуры) и его радианной меры требует такого дополнительного разъяснения: угол величина безразмерная, равная «отношению длины дуги к радиусу», а единицы измерения этой безразмерной величины могут быть разными. Например, такой единице измерения угла как градус просто соответствует дуга длиной не в радиус, а в 1/360 часть длины окружности. Другой пример: в морской навигации для измерения углов используется «румб», этой единице измерения соответствует дуга длиной в 1/32 часть окружности. Понимание того факта, что угол — величина безразмерная, весьма важно при анализе размерностей (см. ниже).
Размерные величины можно умножать и делить друг на друга. Так, отношение пройденного расстояния ко времени в пути дает нам новую физическую величину (скорость), размерность которой 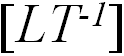 (м/с, км/час и т. п.). При определении размерности величины обычно пользуются размерностями основных, а не производных величин. Складывать и вычитать можно только величины одинаковой размерности (нельзя сложить, например, сантиметры и граммы).
(м/с, км/час и т. п.). При определении размерности величины обычно пользуются размерностями основных, а не производных величин. Складывать и вычитать можно только величины одинаковой размерности (нельзя сложить, например, сантиметры и граммы).
Любой физический закон и описывающее его уравнение не должны зависеть от выбранной нами системы единиц. Это естественно, так как закон природы описывает соотношение между величинами, которое существовало до нас, существует независимо от нас, и будет существовать после нас. А система единиц — дело произвольного соглашения между людьми. Отсюда вытекает очень важное правило:
Обе части любого равенства должны иметь одинаковые размерности.
Написав некое соотношение, всегда можно проверить его правильность путем анализа размерности. Многие студенческие ошибки могут быть выявлены таким путем. Более того, подбором размерностей можно зачастую угадать результат до проведения детальных вычислений.
Приведем пример. Автомобиль трогается с места и движется при этом равноускоренно с ускорением 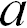 . Какую скорость
. Какую скорость  приобретет автомобиль, пройдя путь
приобретет автомобиль, пройдя путь 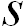 ?
?
Применение анализа размерностей позволяет найти вид искомого соотношения. Скорость является функцией 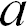 и
и 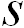 . Это значит, что она выражается как произведение некоторых степеней этих величин:
. Это значит, что она выражается как произведение некоторых степеней этих величин:

где C — некоторая безразмерная постоянная. Надо определить показатели степени 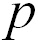 и
и  . Запишем формулу размерности для этого соотношения:
. Запишем формулу размерности для этого соотношения:
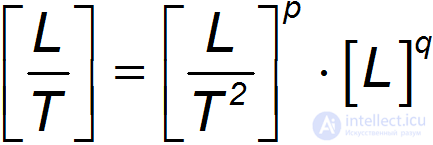
или

В силу того, что семь основных единиц являются независимыми, для согласования размерностей обеих частей равенства необходимо, чтобы 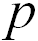 и
и 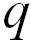 удовлетворяли системе уравнений:
удовлетворяли системе уравнений:
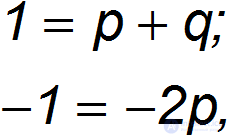
откуда следует:
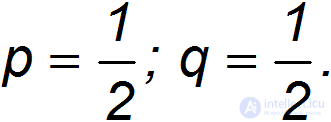
Таким образом, анализ размерностей приводит нас к формуле

Значение безразмерной постоянной C не может быть определено таким способом; при точном решении оно оказывается равным
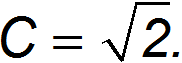
Как правило, значения безразмерных постоянных в физике типа
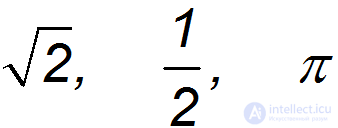
и т. п. не слишком велики и не слишком малы. Поэтому анализ размерностей позволяет оценить масштабы тех или иных физических величин, другими словами, определить их по порядку величины, или, что то же самое, найти их с точностью до множителя порядка единицы типа приведенных (для примера) выше.
Применение анализа размерностей требует осторожности и определенного искусства. Здесь могут встретиться два подводных камня. Первый из них — определение физических величин, от которых может зависеть результат. Для этого требуется понимание, какие физические законы и явления важны для рассматриваемой системы. Второй подводный камень — существование в данной задаче величин, которые могут образовать безразмерные отношения.
Еще один пример, показывающий, как можно ввести в заблуждение и себя и других, если не учесть все, в том числе и безразмерные параметры задачи. Рассмотрим математичес-кий маятник: материальная точка массы  подвешена на невесомой и нерастяжимой нити длины
подвешена на невесомой и нерастяжимой нити длины 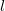 в однородном поле тяжести с ускорением свободного падения
в однородном поле тяжести с ускорением свободного падения 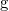 . При отклонении нити от вертикали, благодаря возвращающему действию силы тяжести, возникают колебания. Необходимо оценить период этих колебаний
. При отклонении нити от вертикали, благодаря возвращающему действию силы тяжести, возникают колебания. Необходимо оценить период этих колебаний 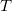 или частоту
или частоту  , которая связана с периодом хорошо известным соотношением
, которая связана с периодом хорошо известным соотношением 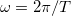 . Из трех параметров
. Из трех параметров 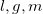 можно составить единственную комбинацию с размерностью частоты, а именно
можно составить единственную комбинацию с размерностью частоты, а именно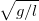 не содержащую массу
не содержащую массу  . Следовательно, (будьте внимательны) частота равна
. Следовательно, (будьте внимательны) частота равна
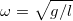
Используя связь частоты и периода, получаем

Это точные выражения для частоты и периода малых колебаний математического маятника. Уже это обстоятельство дает почву для подозрений, так как факт малости колебаний, когда их амплитуда  (
(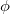 — угол отклонения нити маятника от вертикали) мала:
— угол отклонения нити маятника от вертикали) мала: 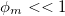 , в приведенной выше оценке нигде и никак не использовался. Точный результат получился случайно благодаря тому, что в выражении для частоты безразмерный коэффициент был без всяких к тому оснований положен равным единице. В действительности в задаче есть четвертый, причем безразмерный параметр — амплитуда колебаний
, в приведенной выше оценке нигде и никак не использовался. Точный результат получился случайно благодаря тому, что в выражении для частоты безразмерный коэффициент был без всяких к тому оснований положен равным единице. В действительности в задаче есть четвертый, причем безразмерный параметр — амплитуда колебаний  , поэтому один только анализ размерностей способен дать лишь следующий результат:
, поэтому один только анализ размерностей способен дать лишь следующий результат:
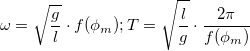
где 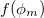 — некоторая функция амплитуды колебаний.
— некоторая функция амплитуды колебаний.
Получить функцию 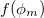 из анализа размерностей невозможно. Решение динамической задачи дает вид этой функции и, в частности, ее значение
из анализа размерностей невозможно. Решение динамической задачи дает вид этой функции и, в частности, ее значение  , которое и следует подставлять в последние, из написанных выше формул для частоты и периода, при условии малости колебаний.
, которое и следует подставлять в последние, из написанных выше формул для частоты и периода, при условии малости колебаний.
Рассмотрим более сложный пример: используя анализ размерностей, найти силу сопротивления  среды движущемуся телу. В этой задаче важно с самого начала определить, от каких величин может зависеть искомая сила. Что нам подсказывает опыт? Чем больше скорость
среды движущемуся телу. В этой задаче важно с самого начала определить, от каких величин может зависеть искомая сила. Что нам подсказывает опыт? Чем больше скорость  движения тела, тем больше сила сопротивления среды. Значит, сила
движения тела, тем больше сила сопротивления среды. Значит, сила  должна зависеть от скорости движения. Далее, тела с большим поперечным сечением испытывают большее сопротивление, чем с меньшим. Поэтому в ответ должна войти площадь
должна зависеть от скорости движения. Далее, тела с большим поперечным сечением испытывают большее сопротивление, чем с меньшим. Поэтому в ответ должна войти площадь  поперечного сечения тела. Наконец, сила
поперечного сечения тела. Наконец, сила  должна зависеть от параметра, характеризующего свойства среды. Здесь и таится первый подводный камень. Какую характеристику среды выбрать?
должна зависеть от параметра, характеризующего свойства среды. Здесь и таится первый подводный камень. Какую характеристику среды выбрать?
Представляется естественным в качестве такого параметра взять плотность (воздуха, жидкости) 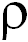 : чем плотнее среда, тем большее влияние она оказывает на движение тела. Исходя из сказанного, мы ищем силу сопротивления в виде
: чем плотнее среда, тем большее влияние она оказывает на движение тела. Исходя из сказанного, мы ищем силу сопротивления в виде

(множитель 2 можно включить в 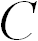 , но мы его выделяем по историческим причинам). Сила имеет размерность произведения массы на ускорение, то есть
, но мы его выделяем по историческим причинам). Сила имеет размерность произведения массы на ускорение, то есть
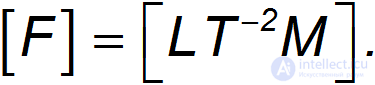
Условие совпадения размерностей обеих частей равенства имеет вид:

откуда следует система уравнений
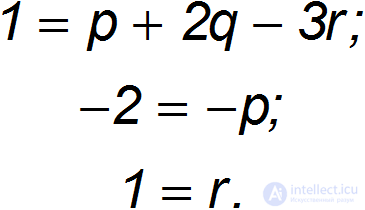
Легко убедиться, что ее решениями являются числа
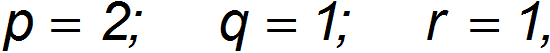
откуда следует искомая формула
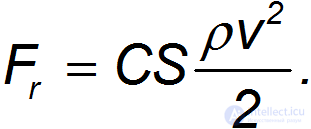
Но почему мы выбрали плотность воздуха в качестве параметра, отвечающего за сопротивление среды? Почему бы в качестве такового не взять величину вязкости воздуха 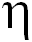 , имеющую размерность
, имеющую размерность  . С вязкостью мы еще познакомимся поближе, а пока достаточно интуитивного представления, что при той же плотности среда может быть более или менее вязкой (кисель и компот). Тогда искомая сила может быть представлена в виде
. С вязкостью мы еще познакомимся поближе, а пока достаточно интуитивного представления, что при той же плотности среда может быть более или менее вязкой (кисель и компот). Тогда искомая сила может быть представлена в виде

Напишем аналогичное условие равенства размерностей:

откуда следует система уравнений
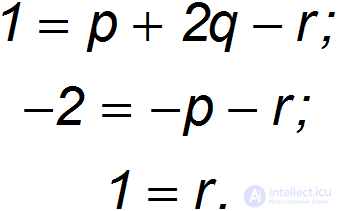
Ее решением являются числа

то есть искомая формула имеет вид:
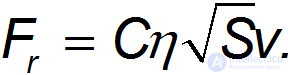
Полученные формулы для силы сопротивления совершенно различны: в одной из них сила зависит от скорости квадратично, в другой — линейно. Так какая же из них верна? Данный пример обнажил первый подводный камень: мы должны решить, какой из двух возможных процессов (лобовое сопротивление или вязкость среды) доминирует в конкретной рассматриваемой задаче.
Попробуем перехитрить уравнения: включим в анализ размерности и плотность воздуха, и его вязкость. Будем искать силу сопротивления в виде
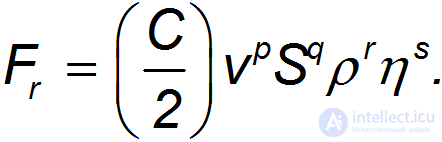
Соотношения размерностей принимают форму:
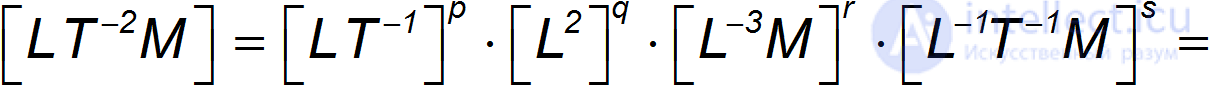
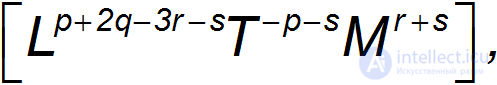
откуда получаем систему уравнений:
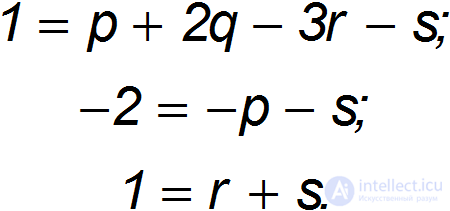
Сразу замечаем, что нас ожидает второй подводный камень: у нас всего три уравнения для определения четырех параметров. Стало быть, какой-то из них останется неизвестным. Попробуем разобраться, что бы это значило? Два последних уравнения позволяют выразить параметры  и
и 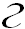 через
через  :
:

Подставляя их в первое уравнение, получаем
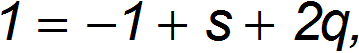
откуда находим
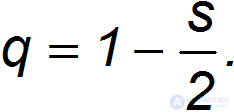
Отсюда получаем силу сопротивления в виде:
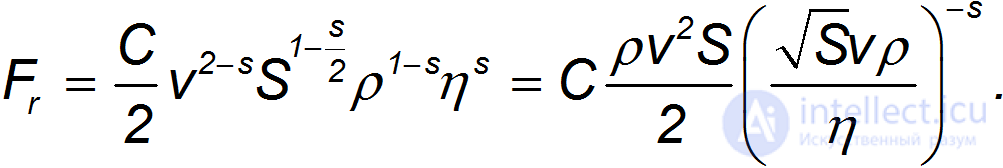
Произвольная степень комбинации в скобках указывает на то, что эта комбинация безразмерна. Раз так, она может быть включена в безразмерную величину 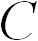 , которая в этом случае оказывается не постоянной величиной, а функцией безразмерного параметра:
, которая в этом случае оказывается не постоянной величиной, а функцией безразмерного параметра:

Этот безразмерный параметр (число Рейнольдса  ) играет важную роль в определении характера силы сопротивления. Функция
) играет важную роль в определении характера силы сопротивления. Функция 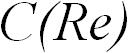 называется коэффициентом сопротивления. Детали мы обсудим позднее, но, забегая вперед, сразу скажем: при малых скоростях воспроизводится второе выражение для силы сопротивления, а при больших — первая формула.
называется коэффициентом сопротивления. Детали мы обсудим позднее, но, забегая вперед, сразу скажем: при малых скоростях воспроизводится второе выражение для силы сопротивления, а при больших — первая формула.
Данный пример демонстрирует, как обращаться с безразмерными комбинациями, если таковые возникают при анализе размерности.
Те задачи, которые мы рассматривали до сих пор, решались по существу одинаково и однозначно. Представим себе, что в какой-то задаче нам необходимо отыскать функциональную зависимость между N физическими величинами. Предполагая, что эта зависимость имеет степенной характер, мы можем пытаться решить задачу методом размерностей. При этом если размерности всех N физических величин выражаются через размерности основных величин и если при этом N – 1 = K (где K — количество основных величин), то существует единственная формула, задающая степенную зависимость между N физическими величинами, и эта формула может быть найдена методом размерностей. Общий вид искомой формулы мы записываем так: в левой части стоит одна из N физических величин в первой степени, а в правой — произведение степеней всех остальных (N – 1) физических величин. Показатели степеней являются неизвестными. Всего неизвестных показателей тоже N – 1. Для определения этих показателей нам необходимо (N – 1) уравнений. Каждое из уравнений мы получаем, сравнивая показатели степени, стоящие слева и справа при одной из основных размерностей. Если в нашей задаче встречаются (N - 1) основных размерностей, мы получим ровно столько уравнений, сколько нам требуется. Эти уравнения линейные, а существование и единственность решения системы таких уравнений гарантирует нам существование и единственность искомой степенной формулы.
Однако, возможны ситуации, когда правило N – K = 1 не выполняется, и тогда приходится прибегать к новым подходам. Рассмотрим простую задачу, чтобы проиллюстрировать такой подход:
Какова дальность полета тела, брошенного под углом 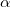 к горизонту с начальной скоростью
к горизонту с начальной скоростью  . Мы предлагаем читателю проделать простые вычисления, прежде чем читать учебник дальше.
. Мы предлагаем читателю проделать простые вычисления, прежде чем читать учебник дальше.
Попытаемся найти связь между S,  и углом
и углом 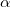 с помощью размерностей. Искомая величина дальность, полета S, может зависеть от начальной скорости бросания
с помощью размерностей. Искомая величина дальность, полета S, может зависеть от начальной скорости бросания  , угла бросания, и, несомненно, от ускорения свободного падения
, угла бросания, и, несомненно, от ускорения свободного падения  (ср. эксперимент по движению тела под углом к горизонту на различных планетах). От массы тела ответ зависеть не должен — размерность искомой величины не содержит размерности «масса».
(ср. эксперимент по движению тела под углом к горизонту на различных планетах). От массы тела ответ зависеть не должен — размерность искомой величины не содержит размерности «масса».
Таким образом, у нас есть четыре величины — S,  ,
, 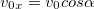 и
и  , зависимость между которыми мы пытаемся установить. В выражения же для размерностей всех этих величин входят только метры и секунды, т. е. N = 4, k = 2 и N – K = 2 > 1. Если записать
, зависимость между которыми мы пытаемся установить. В выражения же для размерностей всех этих величин входят только метры и секунды, т. е. N = 4, k = 2 и N – K = 2 > 1. Если записать
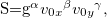
то для трех неизвестных чисел  мы можем написать только два уравнения. Как же решить эту проблему?
мы можем написать только два уравнения. Как же решить эту проблему?
Давайте введем отдельные единицы для измерения расстояний по вертикали и по горизонтали: расстояния вдоль горизонтальной оси 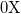 будем измерять в «горизонтальных» метрах —
будем измерять в «горизонтальных» метрах — 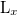 , а расстояния вдоль вертикальной оси Y — в «вертикальных» метрах —
, а расстояния вдоль вертикальной оси Y — в «вертикальных» метрах — 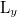 . Тогда размерности таковы:
. Тогда размерности таковы:
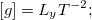
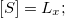

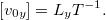
Теперь для N = 4 физических величин уже K = 3 — основными размерностями стали 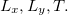
Формула 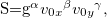
Приводит к соотношению
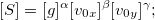

Система уравнений

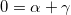
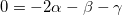
имеет единственное решение
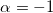
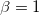

и мы получаем искомый ответ

(Сравните это решение с тем, которое получилось у вас при точном вычислении: 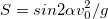 ).
).
Коль скоро мы говорим об измерениях расстояний и времени и выбрали соответствующие единицы (метры, секунды), мы должны условиться, относительно чего мы определяем эти пространственные и временные дистанции. Положение объекта может быть определено только по отношению к каким-то другим телам. Говорить о движении объекта, то есть об изменении его положения, мы можем, только если указываем тела, относительно которых это положение определено.
Тела, которые выбраны для определения положений всех остальных объектов, называются телами отсчета.
В качестве тела отсчета можно, выбрать произвольное твердое тело, например, три взаимно перпендикулярных стальных стержня (рис. 1.10). Далее, на теле отсчета выделяют точку, называемую началом отсчета 0 и выбирают единицы измерения расстояний (в СИ — метры).
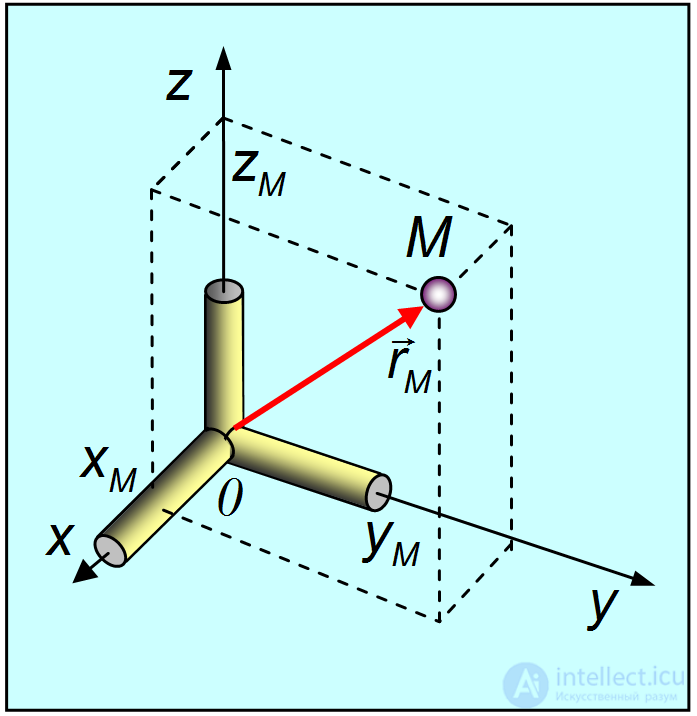
Рис. 1.10. Тело отсчета
В повседневной практике естественным телом отсчета является наша Земля. Но этот выбор не является единственно возможным. Часто удобно пользоваться другими телами отсчета, например Солнцем или звездами. По отношению к разным телам отсчета одни и те же объекты совершают различные движения. Достаточно вспомнить спор относительно двух астрономических систем — Птолемея и Коперника. Обе эти системы правильные и отличаются они, в сущности, лишь выбором тел отсчета, выбор Коперником Солнца кардинально упростил описание движения планет, именно в этом и состоит его заслуга: в средние века требовалась немалая смелость для выбора Солнца, а не Земли в качестве тела отсчета, можно было и на костер попасть.
После выбора тела отсчета положение какой-либо точки М в пространстве может быть задано с помощью направленного отрезка (радиус-вектора 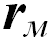 ), соединяющего начало отсчета 0 с данной точкой М. Но вектор — абстрактно-математическое понятие, физическим смыслом оно наполняется, когда мы вводим систему координат. Это может быть декартова прямоугольная система — три взаимно перпендикулярных оси, точка пересечения которых совмещена с началом отсчета. В этом случае радиус-вектор задается тремя проекциями
), соединяющего начало отсчета 0 с данной точкой М. Но вектор — абстрактно-математическое понятие, физическим смыслом оно наполняется, когда мы вводим систему координат. Это может быть декартова прямоугольная система — три взаимно перпендикулярных оси, точка пересечения которых совмещена с началом отсчета. В этом случае радиус-вектор задается тремя проекциями  ,
, 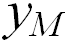 ,
,  данной точки М на координатные оси, которые называются компонентами вектора
данной точки М на координатные оси, которые называются компонентами вектора 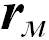 . Это может быть сферическая, цилиндрическая или любая другая система координат, где тот же радиус-вектор
. Это может быть сферическая, цилиндрическая или любая другая система координат, где тот же радиус-вектор 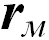 будет задан тройкой других чисел. Число три — это размерность нашего пространства, то есть число независимых координат, необходимых для определения положения точки. Для определения координат точки необходим прибор для определения расстояний, который мы условно будем называть линейкой. В действительности это может быть и деревянная школьная линейка и лазерный дальномер и что угодно другое, способное с требуемой точностью измерять расстояния.
будет задан тройкой других чисел. Число три — это размерность нашего пространства, то есть число независимых координат, необходимых для определения положения точки. Для определения координат точки необходим прибор для определения расстояний, который мы условно будем называть линейкой. В действительности это может быть и деревянная школьная линейка и лазерный дальномер и что угодно другое, способное с требуемой точностью измерять расстояния.

Система координат Декарта
Для отсчета времени нам необходимы какие-то периодические процессы, происходящие в природе или устройствах, созданных человеком. Такие процессы (устройства с такими процессами) мы будем называть часами. При решении любой задачи надо условиться о выборе начала отсчета времени. Начало отсчета времени выбирается произвольно: можно отсчитывать время от сотворения мира, или от основания Рима, или от Рождества Христова, или от бегства Магомета из Мекки и т. д. Как и, практически, всегда произвольность выбора приводит к тому, что он — выбор может быть сделан удачно, менее удачно и совсем неудачно. Удачно – не удачно определяется тем, насколько простым, наглядным и прозрачным получается решение рассматриваемой задачи. В отличие от трехмерного пространства время одномерно, поэтому в дополнение к началу отсчета времени достаточно выбрать лишь единицы измерения (секунды).
Для отсчета времени нам необходимы какие-то периодические процессы, происходящие в природе или устройствах, созданных человеком. Такие процессы (устройства с такими процессами) мы будем называть часами. При решении любой задачи надо условиться о выборе начала отсчета времени. Начало отсчета времени выбирается произвольно: можно отсчитывать время от сотворения мира, или от основания Рима, или от Рождества Христова, или от бегства Магомета из Мекки и т.д. Как и, практически, всегда произвольность выбора приводит к тому, что он — выбор может быть сделан удачно, менее удачно и совсем неудачно. Удачно — не удачно определяется тем, насколько простым, наглядным и прозрачным получается решение рассматриваемой задачи. В отличие от трехмерного пространства время одномерно, поэтому в дополнение к началу отсчета времени достаточно выбрать лишь единицы измерения (секунды).
Тело отсчета, снабженное системой координат и часами, называют системой отсчета..
Пример системы отсчета приведен на рис. 1.11.

Рис. 1.11. Система отсчета
Систему отсчета часто отождествляют с системой координат, что практически никогда не приводит к недоразумениям. Однако надо понимать, что это все-таки не одно и то же: при одном и том же теле отсчета, линейке и часах система координат может быть декартовой, сферической или какой угодно другой.
В классической механике, которую сформулировал в современном виде И. Ньютон, предполагается абсолютный характер пространства и времени. Иначе говоря, в классической механике считается, что измеряемые расстояния и интервалы времени не зависят от выбора системы отсчета. Скажем, если в системе отсчета, связанной с Землей, расстояние от Москвы до Таллина составляет 860 км, то предполагается, что таким же будет результат измерений, проведенных по отношению к системе отсчета, связанной со звездами. Эти положения, кажущиеся столь естественными, вытекают, строго говоря, только из нашего практического опыта, ограниченного сравнительно небольшими расстояниями, временами и малыми скоростями. Впоследствии они были пересмотрены теорией относительности.
Как известно, бывают величины скалярные, не имеющие направления, а бывают векторные, которым кроме величины приписывается некое направление. Время — величина скалярная, а положение в пространстве надо задавать векторами. Недостаточно сказать, что лекция состоится в 860 км от Таллинна. Этой информации не хватит, чтобы узнать, где именно: в Москве или, скажем, в Копенгагене. Отсюда ясно, что векторы должны играть важную роль в физике. Недаром векторное исчисление получило современный вид именно благодаря работам физиков (Дж. Гиббс). Кроме длины и направления, для векторов определяются операция умножения вектора на действительное число и операция сложения векторов, то есть задается векторная алгебра.
Использование векторного исчисления удобно тем, что многие соотношения получаются в общем компактном виде и без особого труда могут быть трансформированы в соответствующие соотношения для любой системы координат. Соотношения между векторами остаются неизменными при смене начала отсчета или выборе иной системы координат. В этом разделе мы напомним некоторые правила векторной алгебры. Занимаясь сейчас физикой, мы не стремимся к точным математическим доказательствам.
Пусть нам дана какая-то декартова прямоугольная система координат. Любой вектор A можно задать тремя компонентами 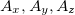 — проекциями вектора на оси
— проекциями вектора на оси  ,
,  ,
,  .В дальнейшем мы используем обе общепринятых записи векторов, выделяя соответствующую букву жирным шрифтом, либо ставя над ней вектор:
.В дальнейшем мы используем обе общепринятых записи векторов, выделяя соответствующую букву жирным шрифтом, либо ставя над ней вектор:
Модулем вектора А (или его длиной) называется число:
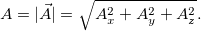
Длина вектора не меняется при поворотах системы координат.
Произведение вектора А на число  является вектором
является вектором
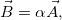
проекции которого определяются как
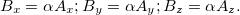
Отсюда следует, во-первых, что длина вектора B равна длине вектора A, умноженной на абсолютное значение числа 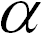
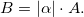
Во-вторых, векторы A и 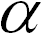 A коллинеарны и имеют одно направление, если
A коллинеарны и имеют одно направление, если 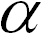 >0, и противоположное, если
>0, и противоположное, если  <0.
<0.
Суммой двух векторов A и B называется вектор с
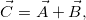
чьи компоненты определяются как сумма компонент слагаемых
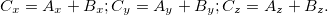
Отсюда следует геометрическое представление суммы векторов — правило параллелограмма либо правило треугольника (рис. 1.12).
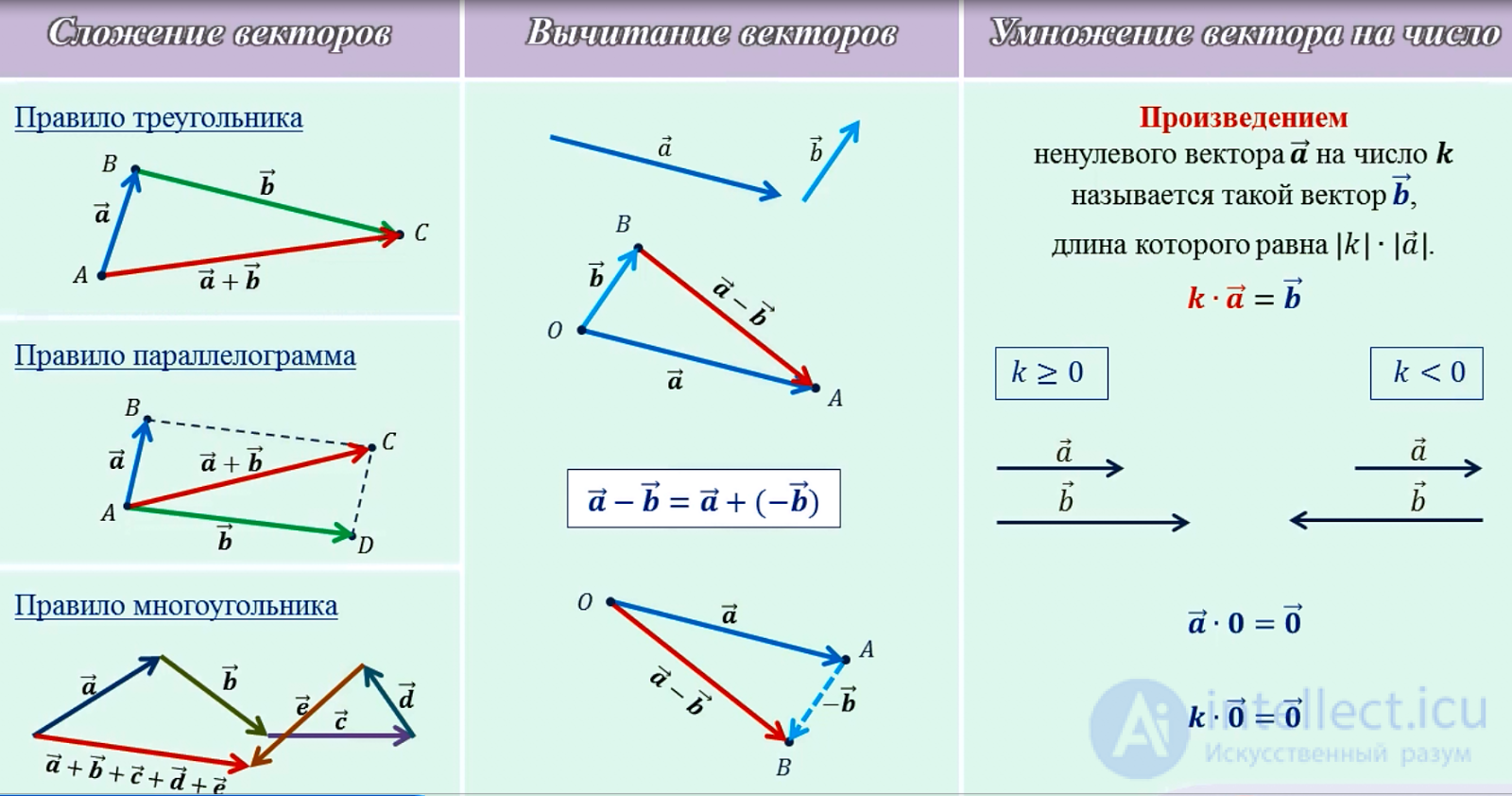

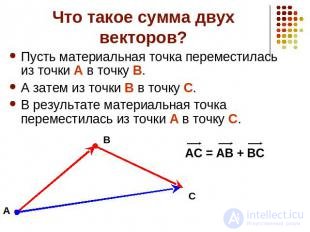
Рис. 1.12. Сложение двух векторов
Аналогично для вычитания векторов
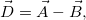
где
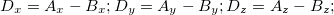
Правило вычитания векторов иллюстрируется на рис. 1.13.
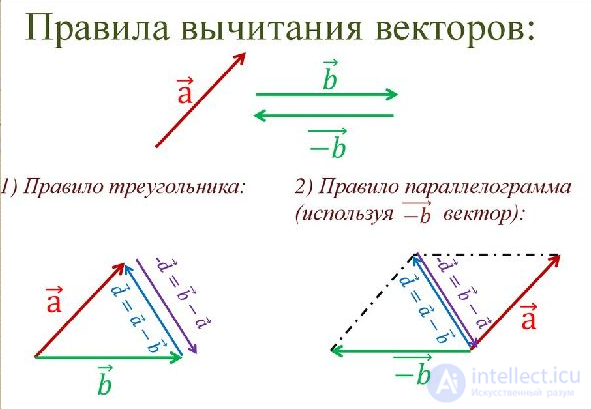
Рис. 1.13. Вычитание векторов
Единичный вектор n — это вектор с длиной, равной единице
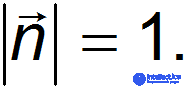
Единичный вектор nA в направлении какого-то вектора а равен

Особую роль играют единичные векторы вдоль положительных направлений осей 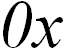 ,
,  ,
, 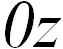 системы координат.
системы координат.
Единичные векторы вдоль положительных направлений осей 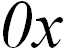 ,
, 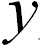 ,
, 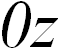 системы координат
системы координат
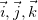
называются ортами.Совокупность ортов состовляет базис данной системы координат.
Иногда оси маркируются цифрами (1,2,3 ) или индексами соответствия осям (x,y,z) обозначают так
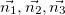 или
или 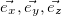
Любой вектор а можно представить в виде разложения по базису
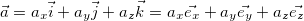
На рис. 1.14 показано разложение вектора вдоль координатных осей
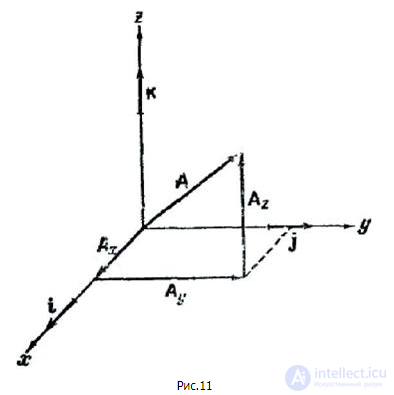
Рис. 1.14. Разложение вектора вдоль координатных осей
Скалярное произведение двух векторов а и b — это число, равное сумме произведений одноименных проекций векторов — сомножителей
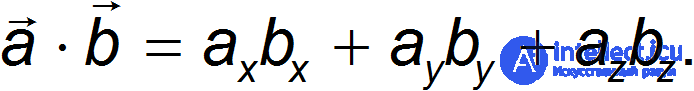
Отсюда следует, что скалярное произведение вектора на самого себя равно квадрату длины вектора

Второе следствие: скалярное произведение коммутативно, то есть

Справедливо также соотношение
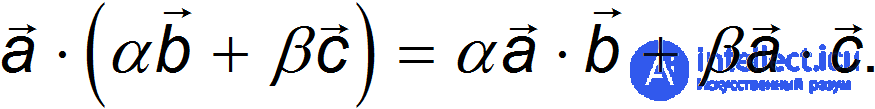
Скалярное произведение не зависит от поворотов системы координат. Можно систему повернуть так, чтобы оба вектора лежали в плоскости  и ось
и ось  была направлена вдоль вектора а. В этой повернутой системе координат векторы-сомножители имеют следующие проекции:
была направлена вдоль вектора а. В этой повернутой системе координат векторы-сомножители имеют следующие проекции:
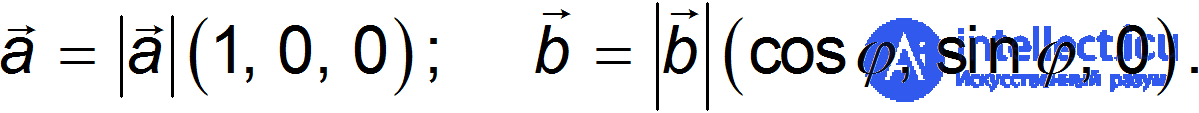
Поэтому скалярное произведение может быть также представлено в виде
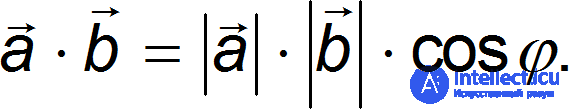
Здесь  — угол между векторами а и b.
— угол между векторами а и b.
Если векторы ортогональны, то есть
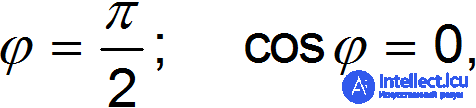
то скалярное произведение равно нулю:
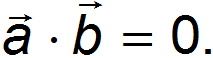
Обратно: если скалярное произведение равно нулю, то либо один из сомножителей — вектор нулевой длины, либо они ортогональны.
Рис. 1.15. Скалярное произведение
Приведем пример использования скалярного произведения (рис. 1.16). Пусть
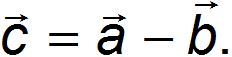
Возведем в квадрат обе части равенства:
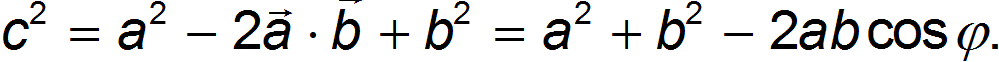
Это — так называемая теорема косинусов; в частном случае прямоугольного треугольника 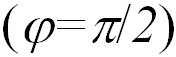 из нее следует теорема Пифагора.
из нее следует теорема Пифагора.
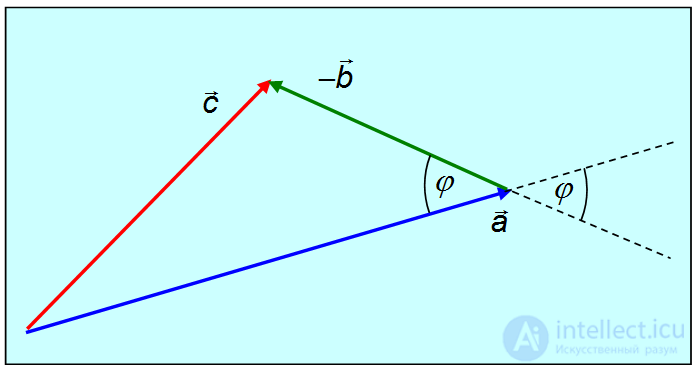
Рис. 1.16. Теорема косинусов
Векторное произведение двух векторов а и b — это вектор с, чьи компоненты равны
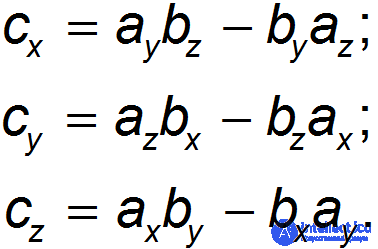
Отсюда следует, что разложение векторного произведения по базису может быть представлено в виде определителя
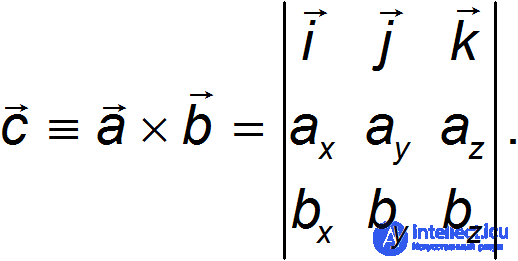
(1.5.1)
Для обозначения векторного произведения используется либо косой крест между сомножителями, либо помещение разделенных запятой (запятая необязательна, если и без нее ясно, где кончается первый сомножитель и начинается второй) сомножителей в квадратные скобки.
Видно также, что в векторном произведении важен порядок сомножителей
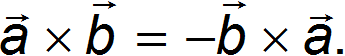
Справедливо соотношение
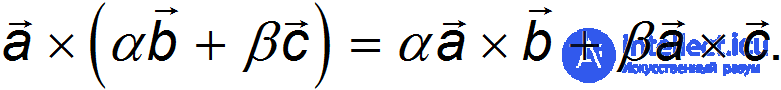
Чтобы понять, куда направлено векторное произведение и чему равна его длина, снова повернем систему координат так, чтобы плоскость осей  совпала с плоскостью векторов а и b и ось
совпала с плоскостью векторов а и b и ось  была направлена вдоль вектора а. Тогда
была направлена вдоль вектора а. Тогда
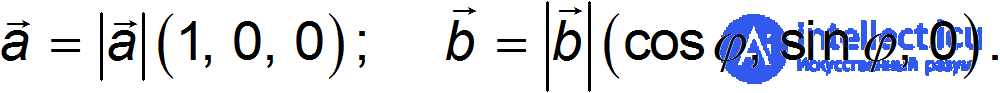
Подставляя эти значения в определитель (1.5.1) для векторного произведения, получаем
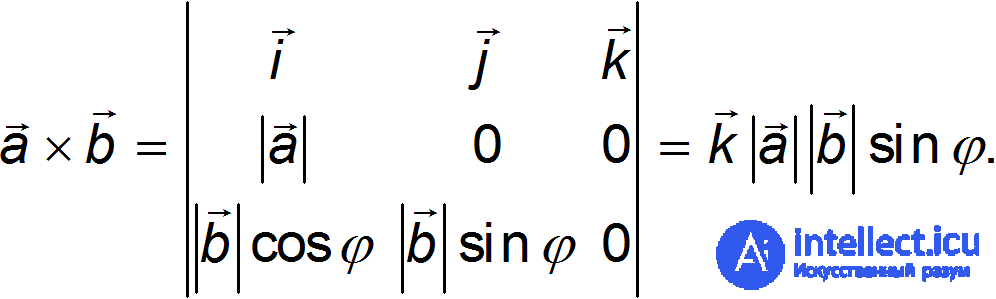
Это значит, что длина векторного произведения равна

и оно ортогонально обоим сомножителям а и b, причем направление его определяется по правилу правого винта.
Если правый винт вращается от первого вектора — сомножителя ко второму по кратчайшему пути, то этот винт перемещается по направлению их векторного произведения.
Применение правила буравчика иллюстрируется на рис. 1.17.
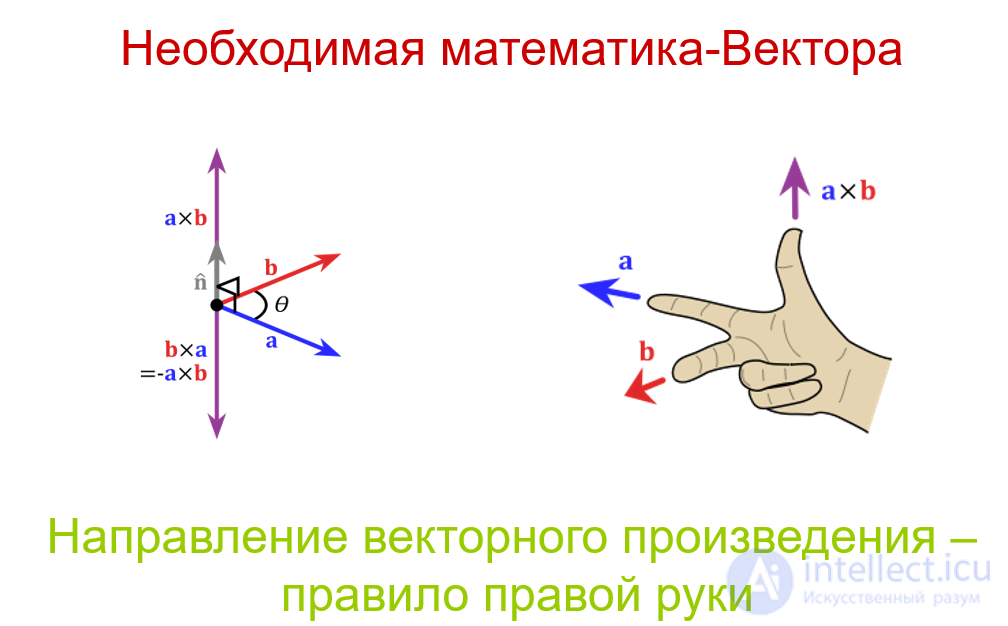
Рис. 1.17. Правило буравчика для определения направления векторного произведения
\
Если сомножители векторного произведения коллинеарны ( ,
,  ;
; 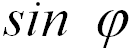 = 0), то векторное произведение равно нулю. Обратно, из равенства нулю векторного произведения вытекает, что либо векторы — сомножители коллинеарны, либо один из векторов равен нулю.
= 0), то векторное произведение равно нулю. Обратно, из равенства нулю векторного произведения вытекает, что либо векторы — сомножители коллинеарны, либо один из векторов равен нулю.
Операция деления на вектор не определена.
Производная вектора a — это вектор, чьи компоненты равны производным от соответствующих компонент вектора а.
Пусть, например, вектор а зависит от времени t. Тогда
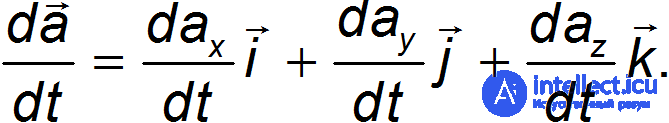
Производные от скалярного и векторного произведений выглядят обычным образом:
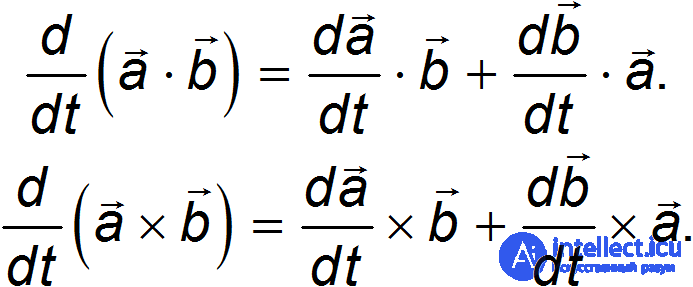
Подчеркнем, что в выражении для производной векторного произведения необходимо сохранять исходный порядок сомножителей.
Необходимая математика-Дифференцирование
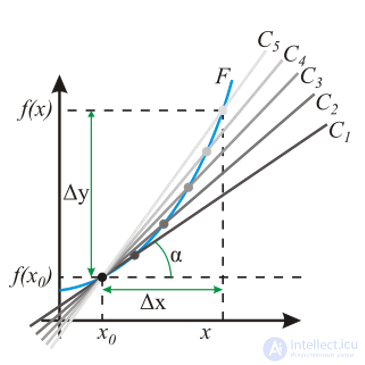
Определение производной

Геометрический смысл производной – касательная в точке x
Правила Дифференцирования

Примеры производных
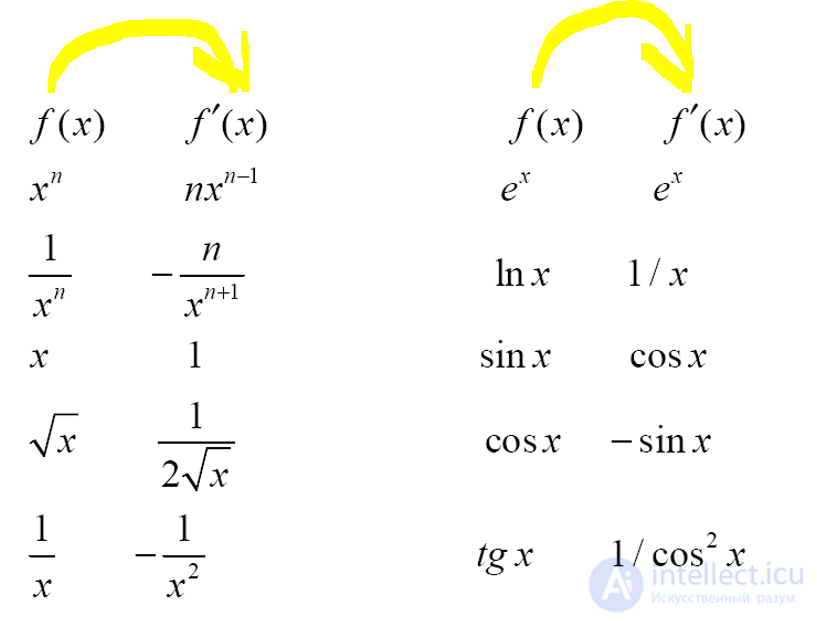
Необходимая математика-Интегрирование
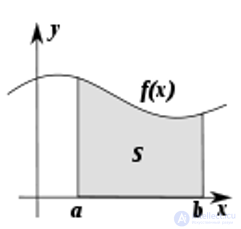
Определение интеграла

Определенный интеграл как площадь под кривой
Вычисление определенного интеграла
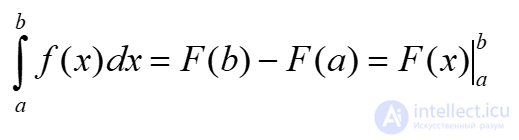
Таблица неопределенных интегралов

Исследование, описанное в статье про математика в физике, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое математика в физике и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики