4.2. Работа механическая кратко

Сразу хочу сказать, что здесь никакой воды про работа, и только нужная информация. Для того чтобы лучше понимать что такое работа, механическая работа , настоятельно рекомендую прочитать все из категории Физические основы механики.

Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.

Механическая работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел) .

При постоянной силе и прямолинейном движении материальной точки, работа рассчитывается как произведение величины силы на перемещение и на косинус угла между векторами перемещения и силы: . В более сложных случаях (непостоянная сила, криволинейное движение) это соотношение применимо к малому промежутку времени, а для вычисления полной работы необходимо суммирование по всем таким промежуткам.

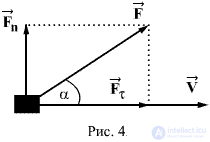
Если рассматриваемая сила 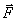постоянна,а тело, к которому она приложена, движется поступательно и прямолинейно, то работой, совершаемой силой при прохождении телом пути 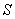, называют величину

(4.1)

где а - угол между силой 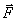и направлением движения тела.

Работа - скалярная величина. Если вектор силы и вектор перемещений образуют острый угол т.е. , то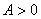, если 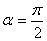, то 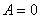, т.е. сила, действующая перпендикулярно к перемещению тела, работы не совершает.

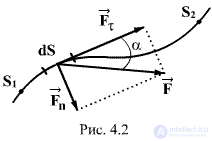
В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.4.2). Выделим элементарный участок пути 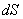, на котором силу можно считать постоянной и перемещение прямолинейным. Элементарная работа на этом участке равна

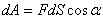(4.2)

Полная работа на пути определяется интегралом

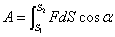(4.3)

Определение работы

По определению, «элементарная» (совершаемая за бесконечно малое время) работа — скалярное произведение действующей на материальную точку силы на перемещение , то есть

.

Работа за конечный промежуток времени — интеграл элементарной работы:

.

Если имеется система материальных точек, выполняется суммирование по всем точкам. При наличии нескольких сил их работа определяется как работа равнодействующей (векторной суммы) этих сил.

Обозначения, размерность

Работа обычно обозначается заглавной буквой (от нем. Arbeit — работа, труд) или заглавной буквой (от англ. work — работа, труд).

Единицей измерения (размерностью) работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг. При этом

1 Дж = 1 кг·м²/с² = 1 Н·м;

1 эрг = 1 г·см²/с² = 1 дин·см;

1 эрг = 10⁻⁷ Дж.

Вычисление работы

Случай одной материальной точки

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершенного точкой:

Здесь «» обозначает скалярное произведение, — вектор перемещения.

Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа этой силы равна нулю.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки :

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из перемещений , если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат , интеграл определяется следующим образом:

,

где и — радиус-векторы начального и конечного положения тела. Об этом говорит сайт https://intellect.icu . Например, если движение происходит в плоскости , а и (, — орты), то последний интеграл обретет вид , где производная берется для кривой , по которой движется точка.

Если сила является консервативной (потенциальной), результат вычисления работы будет зависеть только от начального и финального положения точки, но не от траектории, по которой она перемещалась.

Случай системы точек или тела[править | править код]

Работа сил по перемещению системы из материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершенные над каждой точкой системы, суммируются в работу этих сил над системой):

.

Если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл:

,

где — работа по перемещению бесконечно малого фрагмента объема тела , локализованного около координаты (в системе отсчета тела), от начального до финального положения, (Н/м³) — плотность действующей силы, а интегрирование проводится по всему объему тела.

Эти формулы могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Работа и кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

С использованием второго закона Ньютона, позволяющего выразить силу через ускорение как (где — масса материальной точки), а также соотношений и , элементарная работа может быть переписана как

.

При интегрировании от начального до финального момента получится

,

где — кинетическая энергия. Для материальной точки она определяется как половина произведения массы этой точки на квадрат ее скорости и выражается как . Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Работа и потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая, что

.

Здесь — оператор набла. Если все силы, действующие на частицу, консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, то

.

Данный результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия

в замкнутой системе, в которой действуют консервативные силы, является постоянной во времени. Этот закон широко используется при решении задач классической механики.

Работа силы в теоретической механике

Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, , и на нее действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее).

Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

.

Если положение точки на траектории ее движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из последней формулы получится

.

Вау!! 😲 Ты еще не читал? Это зря!

• Закон сохранения энергии
• Механическая энергия
• Теорема о кинетической энергии системы
• Механические приложения криволинейных интегралов
• Работа в термодинамике

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про работа Надеюсь, что теперь ты понял что такое работа, механическая работа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики

Из статьи мы узнали кратко, но содержательно про работа