3.9. Универсальная форма второго закона Ньютона, выраженная через импульс системы

Сразу хочу сказать, что здесь никакой воды про универсальная форма второго закона ньютона выраженная через импульс системы, и только нужная информация. Для того чтобы лучше понимать что такое универсальная форма второго закона ньютона выраженная через импульс системы , настоятельно рекомендую прочитать все из категории Физические основы механики.

Используя выражеие для импульса

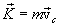
и второй закон Ньютона можем записать

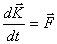(3.11)

где - главный вектор всех внешних сил, действующих на систему.

Последнее уравнение является обобщением уравнения импульса на произвольную механическую систему, т.к. Об этом говорит сайт https://intellect.icu . ее всегда можно представить, в виде системы материальных точек, взаимодействующих друг с другом и с внешними телами. Внешними телами называются тела, не входящие в состав рассматриваемой системы, а силы, действующие на систему со стороны этих тел - внешними силами. Соответственно силы взаимодействия между материальными точками, принадлежащими рассматриваемой системе называются внутренними силами, и их равнодействующая равна нулю. Уравнение (3.11) показывает, что скорость изменения импульса механической системы равна главному вектору всех внешних сил, действующих на эту систему.

Статью про универсальная форма второго закона ньютона выраженная через импульс системы я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое универсальная форма второго закона ньютона выраженная через импульс системы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики