6.1. Преобразования Лоренца

Сразу хочу сказать, что здесь никакой воды про преобразования лоренца, и только нужная информация. Для того чтобы лучше понимать что такое преобразования лоренца , настоятельно рекомендую прочитать все из категории Физические основы механики.

Исходя из сформулированных выше постулатов теории относительности Эйнштейна, можно найти законы преобразований, связывающие межу собой пространственные координаты и время в двух системах отсчета, движущихся прямолинейно и равномерно относительно друг друга.

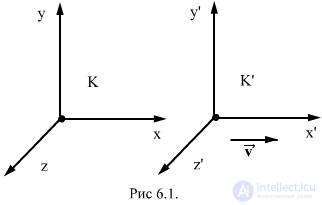
Пусть х, у, z, и х’, у’, z’ и t’,- координаты и время в инерциальных систем отсчета K и K’, а v - скорость их относительного движения (рис. 6.1).

При этом нет никаких оснований полагать, что время в системе  совпадает со временем в системе K, как это безоговорочно принималось в классической физике. Для просторы выкладок выберем направление скорости за направление осей х и 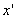. Предположим, что в некоторый момент времени t’ в точке скоординатами происходит некоторый физический процесс, который назовем событием. Нашей задачей является нахождение «координат» события в системе отсчета K’, т.е. нахождение величин х, y, z, t, характеризующих тот же физический процесс в системе K.

Выберем за начало отсчета времени t=0 тот момент, в который начало координат системы K’ совпадало с началом координат системы K. Пусть в момент времени t=0 из начала координат начала распространяться сферическая электромагнитная волна (рис.6.2). В системе K уравнение волновой поверхности имеет вид.

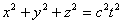
или

(6.1)

Поскольку, согласно принципу относительности Эйнштейна, закон и величина скорости распространения волны должны быть одинаковыми во всех инерциальных системах отсчета, наряду с этим уравнением с равным правом можно написать уравнение сферической волны в системе K’.

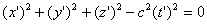
Так как в начальный момент времени начало координат систем совпадали, то

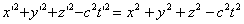(6.2)

Формулы преобразования координат и времени должны, во-первых, не нарушать соотношений (6.1) и (6.2), а, во-вторых, быть линейными. Об этом говорит сайт https://intellect.icu . Требования линейности связано с однородностью пространства. Т.к. движение системы K’ происходит только вдоль оси х преобразование координат у и z должно иметь вид

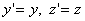
Закон преобразования х’ через х можно написать, исходя из следующегосоображения: если в момент времени t=0 начала систем координат K и K’ совпадали, то координата плоскости х’ в системе K запишется х=νt. Следовательно, в самом общем случае можно написать

(6.3)

где коэффициент 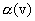 может зависеть лишь от скорости относительного движения. Не делая никаких произвольных допущений о совпадении времени в двух системах отсчета, мы можем представить t’ в виде линейной однородной функции х и t

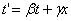(6.4)

Kоэффициенты  и 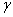 могут, вообще говоря, зависеть от скорости v. Если бы оказалось, что 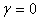, а 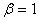, то мы вернулись бы к преобразованиям Галилея. Для определения коэффициентов ,  и 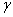, отвечающих Требованиям принципа относительности Эйнштейна, мы должны подставить (6.3) и (6.5) в (6.2). Это дает

Для выполнения тождества необходимо приравнять коэффициенты при х²,t²и хt. Раскрыв скобки и проведя соответствующие преобразования получим:

Из этих трех уравнений находим неизвестные величины ,  и ,: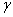

При этом всюду мы выбрали положительный знак корня. Подставляя значения ,  и 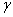 в преобразования координат (6.3) и (6.4) находим:

(6.5)

Эти формулы носят название преобразований Лоренца. Формулы обратного преобразования от штрихованных к не штрихованным величинам:

(6.6)

преобразования лоренца приводят к выводам, коренным образом противоречащим привычным представлениям о свойствах времени и пространства, сложившимся на основе повседневного опыта. Рассмотрим несколько примеров применения преобразований Лоренца.

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про преобразования лоренца Надеюсь, что теперь ты понял что такое преобразования лоренца и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики