Лекция
Привет, Вы узнаете о том , что такое рывок, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое рывок, четвертая, пятая и шестая производные перемещения , настоятельно рекомендую прочитать все из категории Физические основы механики.
рывок — векторная физическая величина, характеризующая темп (скорость) изменения ускорения тела. Является третьей производной по времени от радиус-вектора.
| Единицы измерения | |
|---|---|
| СИ | м/с3 |
| СГС | см/с3 |
| Другие единицы | g/с |
Вектор рывка 
в любой момент времени находится путем дифференцирования вектора ускорения частицы по времени:
где:
— ускорение,
— скорость,
— радиус-вектор.
Соответственно формулы для движения с постоянным рывком имеют вид:
Формулы можно обобщать и далее на более высокие производные радиус-вектора, вводя в разложение координаты в степенной ряд все новые и новые члены. По традиции или просто для удобства из-за частого использования первые 3 коэффициента в разложении имеют собственные названия: скорость, ускорение и рывок соответственно.
Сила, действующая на ускоренно движущийся заряд (радиационное трение, или реакция излучения), пропорциональна третьей производной координаты (т. e. первой производной ускорения) по времени.
(в системе СИ).
Понятие рывка применяется при перевозке пассажиров, а также хрупких и ценных грузов.
Пассажир приспосабливается к ускорению, напрягая мышцы и подбирая позу. При изменении ускорения поза, естественно, тоже меняется. Пассажиру нужно дать время, чтобы отреагировать и сменить ее — иначе стоячий пассажир потеряет равновесие, а сидячий — ударится. Типичный пример — момент полной остановки вагона метро после процесса торможения: стоячие пассажиры, наклонившиеся вперед в процессе торможения, не успевают приспособиться к новому ускорению, возникающему в момент остановки, и наклоняются назад.
Аналогично, груз, к которому приложено ускорение, деформируется. Частое и быстрое изменение ускорения означает частую и быструю деформацию, что может привести к разрушению хрупкого груза. Частично рывок можно уменьшить, использовав амортизирующую упаковку.
Для многих приборов и устройств в технических условиях нормируется предельное значение рывка.
Производные большего порядка в транспорте применяются редко. Известный случай, когда радиус-вектор исследовался до четвертой производной — вывод на орбиту телескопа Хаббла .
Применяется в интегрировании по Верле для быстрого численного решения дифференциальных уравнений движения материальных точек.
В статье И. И. Смульского и Я. И. Смульского «Астероид Апофис: эволюция орбиты и возможное использование» используются производные до шестого порядка и ряд Маклорена в программе расчета
В работе финского математика К. Зундмана, посвященной решению «задачи трех тел», используются высшие производные и ряды
Понятие рывка находит применение и в задаче о вычислении угловых скоростей и угловых ускорений звеньев шарнирного четырехзвенника — в ситуации, когда все шарниры лежат на одной прямой .
В металлорежущих станках с электронным управлением изменение ускорения также важно — быстрые деформации инструмента, случающиеся при высоком рывке, преждевременно выводят инструмент из строя.
Под ускорением в социальных науках понимают возрастание скорости технического развития, которое для одних (трансгуманисты) есть неизбежный исторический процесс, ведущий к трансформации человеческого, для других — способ существования постфордистского капитализма. Последних можно разделить на два лагеря: это акселерационисты, согласно которым капитализм стимулирует ускорение и одновременно препятствует ему, непрестанно откладывая тем самым подлинно революционные изменения, и различные критики акселерационизма, которые полагают, что ускорение — это параллельная дорога, не совпадающая с революционным путем («Ускориться то ускорилась, а перестроиться не успела»).
Все эти три позиции объединяет реалистическая концепция ускорения: оно рассматривается как существующее в действительности, а не как абстракция, имеющая свою историю. Этому реализму ускорения следует противопоставить номиналистический взгляд: реально существует только какое-то движение вещей (по крайней мере, в гераклитовой вселенной), а скорость и ускорение — лишь способы описывать это движение. Эти способы возникают в ходе развития новоевропейской механики и дифференциального исчисления: скорость — это первая производная пути по времени (радиус-вектора), ускорение — производная скорости (вторая производная от радиус-вектора); оба предполагают систему координат, в которой производится измерение, т.е. восходят к картезинскому изобретению. Это, повторимся, абстракции, описывающие движение, но не само движение.
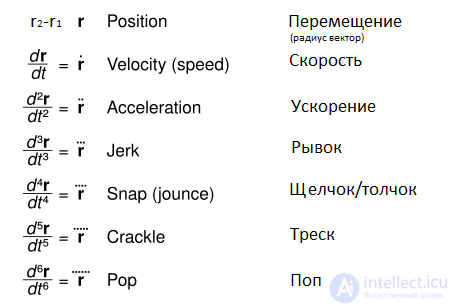
Пролить свет на истинное положение вещей позволяет как раз движение абстракций: есть также имя для третьей производной пути, т.е. для производной самого ускорения, — рывок (jerk). Рывок — это момент начала/конца ускорения/замедления (учитываемый, скажем, при разработке транспортных средств). Более высокие производные радиус-вектора в классической механике не используются, хотя есть условные названия для четвертой, пятой и шестой: Snap, Crackle и Pop (имена гномов — рисованных персонажей с упаковки кукурузных хлопьев), и далее (Lock, Drop, Shot, Put…).
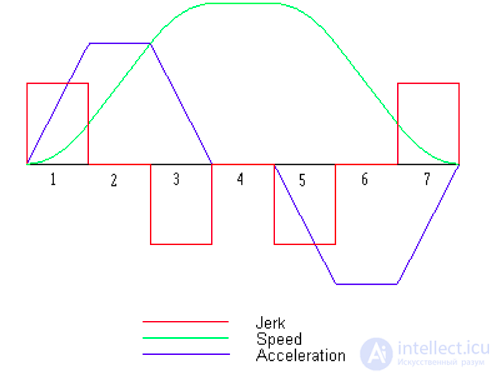
В свете этого расширенного представления о движении можно сказать, что понятие ускорения ограниченно, так как оно заслоняет ускорение самой скорости, изменение ее изменения. Наблюдаемое технологическое развитие при ближайшем рассмотрении состоит скорее из серии рывков, т.е. переходов к «новым открытиям в целой вселенной возможностей», по выражению акселерационистов, и именно эти рывки заключают в себе невидимые микрореволюции (в этом смысле излагаемая здесь позиция является пост-акселерационистской). Однако и такое описание было бы далеко не полным. Если трансгуманисты правы в том, что мы имеем дело с экспоненциальным ускорением, то по мере приближения к бесконечной скорости кривой технологического развития (к технологической сингулярности) мы как бы зумируем (увеличиваем в масштабе) эту кривую, различая в ней все новые и новые производные пути по времени. В каждом рывке уже заключены Щелк, Хрусть и Хлоп, и настоящая наука об изменении (которую Симондон называл аллагматикой) должна исследовать движение этих абстракций, а не социокультурные эффекты (точнее, гомологии) абстракций, взятых самих по себе, будь то скорость или ускорение.
В известном и странном смысле таким исследованием, т.е. зумированием кривой скорости, и занимается информатика. Те моменты движения, которые могут не иметь механического (физического) значения, обретают метафизическое значение в эволюции информатических абстракций. Согласно диалектической схеме развития информатики (см. изданный «Генезис графического пользовательского интерфейса»), исторически первая абстракция — переменная (variable) — есть движение как таковое, т.е. нечто, обладающее скоростью. Это «тезис» первого этапа эволюции, завершающегося «синтезом» в понятии объекта, который становится «тезисом» второго этапа, и т. д. Пост-акселерационистская гипотеза состоит в том, что каждая абстракция, служащая тезисом нового этапа эволюции информатики, соответствует «открытию» следующей производной пути в его социокультурной и техноэкономической проекции.
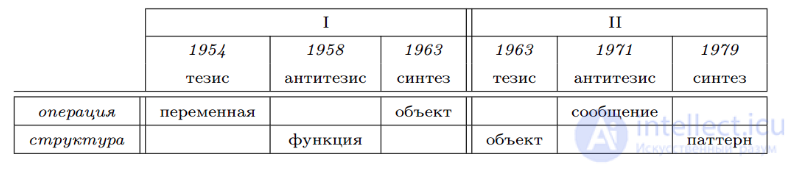
Каждое изобретение новой «тезисной» абстракции в computer science вызывало увеличение скорости программной разработки и одновременно зумирование кривой скорости: переменная (первый этап) — скорость, объект (второй этап) — ускорение, паттерн (третий этап) — рывок. Начало культурной жизни переменной в 1960-х гг. совпадает с жалобами на увеличение «ритма жизни» (скорость), распространение абстракции объекта (с конца 1970-х гг.) — с первыми дискуссиями фантастов и футурологов об ускорении, а внедрение языка паттернов — с софтверным рывком в 1990-х гг. Сегодняшняя ситуация в информатике есть переход от понятия модели в системной инженерии как синтеза третьего этапа (паттерн — онтология — модель) к модели как тезису четвертого этапа, т.е. к четвертой производной пути, которую называют snap («щелчок») или jounce («бросок, толчок»). Этот переход осуществляется через структурное переописание понятия модели при помощи аппарата теории категорий и математической логики. Внедрение этой технологии можно поэтому образно уподобить броску или щелчку («перещелкивание»!), который совпадет с новыми изменениями в общественно-культурной жизни и который будет еще более «быстрым» (т.е. демонстрирующим скорость в еще большем масштабе), чем все предыдущие моменты истории.
Предложенная схема соответствия между движением информатических абстракций и движением дифференцирования радиус-вектора является, разумеется, гадательной, но она может послужить важным мостом между теорией оператóрной рекапитуляции и социальными исследованиями технокультурной эволюции.
В физике четвертая , пятая и шестая производные положения определяются как производные вектора положения по времени – причем первая, вторая и третья производные являются скоростью , ускорением и рывком соответственно. Производные более высокого порядка встречаются реже, чем первые три; поэтому их названия не столь стандартизированы, хотя концепция минимальной траектории щелчка использовалась в робототехнике .
Четвертая производная называется snap , в результате чего пятая и шестая производные иногда «немного шутливо» называются crackle и pop , вдохновленные талисманами Rice Krispies Snap, Crackle и Pop Четвертая производная также называется jounce .
Щелчок или толчок — это четвертая производная вектора положения по времени или скорость изменения рывка по времени.Эквивалентно, это вторая производная ускорения или третья производная скорости , и определяется любым из следующих эквивалентных выражений
В гражданском строительстве проектирование железнодорожных путей и дорог подразумевает минимизацию щелчка, особенно вокруг изгибов с разными радиусами кривизны . Когда щелчк постоянен, рывок изменяется линейно, что позволяет плавно увеличивать радиальное ускорение , а когда, как это предпочтительно, щелчк равен нулю, изменение радиального ускорения линейно. Минимизация или устранение щелчка обычно выполняется с использованием математической функции клотоиды .
Минимизация щелчка улучшает производительность станков и американских горок.
Для постоянного щелчка используются следующие уравнения: 
где
постоянный щелчок,
это начальный рывок,это последний рывок,
начальное ускорение,конечное ускорение,
начальная скорость,конечная скорость,
это начальное положение,это конечная позиция,
время между начальным и конечным состояниями.Обозначениес→(используемый Виссером ) не следует путать с вектором смещения, обычно обозначаемым аналогичным образом.
Размеры щелчка — расстояние в четвертой степени времени (LT −4 ). Об этом говорит сайт https://intellect.icu . Соответствующая единица СИ — метр в секунду в четвертой степени, м/с 4 , м⋅с −4 .
Пятая производная вектора перемещения по времени иногда называется треском. Это скорость изменения щелчка по времени. Треск определяется любым из следующих эквивалентных выражений: 
Для постоянного потрескивания используются следующие уравнения: 
где
: постоянный треск,
: начальный щелчок, : финальный щелчок, : начальный рывок, : финальный рывок, : начальное ускорение, : конечное ускорение, : начальная скорость, : конечная скорость, : исходное положение, : конечная позиция, : время между начальным и конечным состояниями.Размеры трещины составляют LT −5 . Соответствующая единица СИ — м/ с5 .
Шестую производную вектора перемещения по времени иногда называют pop. Это скорость изменения потрескивания по времени. Pop определяется любым из следующих эквивалентных выражений:
Для постоянной поп-музыки используются следующие уравнения 
где
: постоянный хлопок,
: начальный треск, : финальный треск, : начальный щелчок, : финальный щелчок, : начальный рывок, : финальный рывок, : начальное ускорение, : конечное ускорение, : начальная скорость, : конечная скорость, : исходное положение, : конечная позиция, : время между начальным и конечным состояниями.Размерность поп составляет LT −6 . Соответствующая единица СИ — м/с 6 .
Существует широкий спектр приложений для оптимизации траектории, в первую очередь в робототехнике: промышленность, манипуляция, ходьба, планирование пути и аэрокосмическая промышленность. Его также можно использовать для моделирования и оценки.
В зависимости от конфигурации, роботизированные манипуляторы с открытой цепью требуют определенной степени оптимизации траектории. Например, роботизированная рука с 7 сочленениями и 7 звеньями (7-DOF) является избыточной системой, в которой одно декартово положение конечного эффектора может соответствовать бесконечному числу положений углов сочленений, таким образом, эта избыточность может использоваться для оптимизации траектории, чтобы, например, избегать любых препятствий в рабочем пространстве или минимизировать крутящий момент в сочленениях.
Оптимизация траектории часто используется для вычисления траекторий для вертолетов с квадрокоптерами . Эти приложения обычно используют узкоспециализированные алгоритмы. Одно интересное приложение, показанное U.Penn GRASP Lab, вычисляет траекторию, которая позволяет квадрокоптеру пролетать через обруч, когда его бросают. Другое, на этот раз от ETH Zurich Flying Machine Arena , включает два квадрокоптера, бросающих шест вперед и назад между собой, при этом он уравновешивается как перевернутый маятник. Проблема вычисления траекторий с минимальной энергией для квадрокоптера также недавно была изучена
Оптимизация траектории используется в производстве, в частности, для управления химическими процессами или вычисления желаемого пути для роботизированных манипуляторов.
Существует множество различных приложений для оптимизации траектории в области шагающей робототехники. Например, в одной из статей использовалась оптимизация траектории двуногих походок на простой модели, чтобы показать, что ходьба энергетически выгодна для движения с низкой скоростью, а бег энергетически выгоден для движения с высокой скоростью Как и во многих других приложениях, оптимизация траектории может использоваться для вычисления номинальной траектории, вокруг которой строится стабилизирующий контроллер. Оптимизация траектории может применяться в детальном планировании движения сложных гуманоидных роботов, таких как Atlas . Наконец, оптимизация траектории может использоваться для планирования пути роботов со сложными динамическими ограничениями с использованием моделей пониженной сложности.
Для тактических ракет профили полета определяются историями тяги и подъемной силы . Эти истории могут контролироваться рядом средств, включая такие методы, как использование истории команды угла атаки или графика высоты/снижения, которому должна следовать ракета. Каждая комбинация факторов конструкции ракеты, желаемых характеристик ракеты и ограничений системы приводит к новому набору оптимальных параметров управления.
Минимизация ускорения (вторая производная траектории) снижает нагрузку на приводы, уменьшает износ механических частей и повышает точность управления.
Минимизация рывка (третья производная траектории) делает движение плавным, что особенно важно для промышленных манипуляторов и медицинских роботов.
Максимизация скорости (первая производная) используется, когда важно выполнить задачу за минимальное время (например, при сборке на конвейере или в соревновательных роботах).
Минимизация рывка обеспечивает комфорт пассажиров и снижает нагрузку на подвеску автомобиля.
Максимизация скорости применяется для быстрого прибытия к цели, но с учетом ограничений по ускорению и дорожным условиям.
Оптимизация кривизны траектории снижает вероятность заноса, особенно при движении по скользким покрытиям.
В игровых движках и 3D-анимации минимизация рывка делает движение персонажей реалистичным.
Максимизация скорости используется для сцен с резкими рывками или ускорениями (например, при взрывах, прыжках или гонках).
Минимизация ускорения снижает перегрузки на экипаж и конструкцию.
Максимизация скорости и ускорения может быть критически важна при взлете или уклонении от опасности.
В станках с ЧПУ минимизация рывка повышает точность обработки, снижает вибрации.
В логистике максимизация скорости и ускорения используется при быстрой транспортировке грузов, но с учетом ограничений.
В системах транспортировки (конвейеры, автономные тележки, дроны) важно учитывать:
Грузоподъемность – избыточное ускорение или рывок может привести к падению груза.
Балансировка – особенно для неустойчивых объектов (например, налитых жидкостей в цистернах).
Оптимизация времени – максимизация скорости, но с плавными переходами между участками.
Исследование, описанное в статье про рывок, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое рывок, четвертая, пятая и шестая производные перемещения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики