Лекция
Привет, Вы узнаете о том , что такое термодинамика, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое термодинамика, теплоемкость системы, адиабатный процесс , настоятельно рекомендую прочитать все из категории Молекулярная физика и термодинамика.
В отличие от молекулярно-кинетической теории классическая термодинамика изучает макроскопические свойства тел и характеристики различных явлений, не интересуясь их микроскопической природой. Поэтому уже с самого начала она оперирует величинами, характеризующими систему как целое (давление, температура, объем и т. п.). Как правило, термодинамика не в состоянии объяснить значения тех или иных физических параметров, которые определяются экспериментально. В основе термодинамики лежат несколько фундаментальных законов, называемых началами термодинамики. Они были установлены на основании обобщения большой совокупности опытных фактов. Их применение позволяет изучать протекание различных процессов и делать выводы, имеющие общий характер.
Примером функции состояния системы является ее внутренняя энергия U. Она составляется из кинетической энергии хаотического движения молекул, потенциальной энергии взаимодействия между молекулами, кинетической энергии атомов внутри молекул, потенциальной энергии взаимодействия между атомами внутри молекул, а также кинетической и потенциальной энергии частиц, входящих в состав атомов (ядер и электронов). Внутренняя энергия не включает кинетическую и потенциальную энергии, которыми система может обладать как целое (скажем, при движении сосуда с газом или помещении газа во внешнее потенциальное поле). Каждый раз, когда система оказывается в том же состоянии (например, при каких-то конкретных температуре и давлении), ее внутренняя энергия принимает присущее этому состоянию значение, независимо от способа, каким система приведена в данное состояние. При переходе из состояния 1 в состояние 2 изменение внутренней энергии равно разности значений внутренней энергии в этих состояниях
|
|
|
(2.1) |
и также не зависит от того, какие процессы перевели систему из состояния 1 в 2.
Внутренняя энергия системы может изменяться двумя способами:
Совершение работы сопровождается перемещением внешних тел, действующих на систему. Рассмотрим заключенный под поршнем в сосуде газ (рис. 2.1-1).
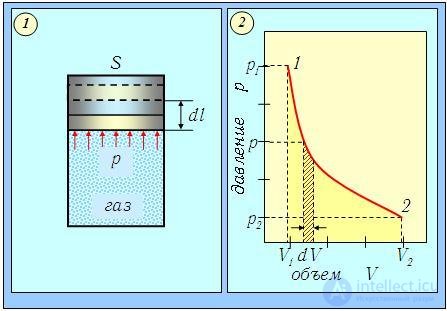
Рис. 2.1. Расширение газа под поршнем (1) и графическое изображение (2) производимой им работы
При перемещении поршня на расстояние dl газ совершает работу
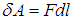
Если S — площадь поперечного сечения сосуда, то силу F можно выразить через давление (F = pS), которое при малом перемещении поршня можно считать постоянным. Перемещение выражается через изменение объема газа
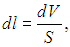
так что элементарная работа, совершенная газом, представляется в виде
|
|
|
(2.2) |
то есть численно равна площади заштрихованного участка на (pV) — диаграмме процесса (рис. 2.1-2).
|
Работа — это мера механической энергии, переданной от одной системы к другой. |
Этот тип передачи энергии всегда связан с перемещением макроскопических частей системы и внешних тел. Если бы такого перемещения не происходило, то есть не менялся бы объем системы (dV = 0), то, как следует из соотношения (2.2), газ не мог бы совершить работы (dА = 0). При увеличении объема системы работа положительна (система совершает работу), а при уменьшении — отрицательна (работа совершается внешними силами над системой).
При конечном изменении объема системы совершаемая газом работа является суммой всех элементарных работ dА и записывается в виде интеграла
|
|
|
(2.3) |
Графически такая работа изображается площадью криволинейной трапеции под графиком процесса на (р,V) — диаграмме (см. рис. 2.2). Видно, что эта площадь зависит не только от положения концевых точек (р1,V1) и (р2,V2), но и от всего характера процесса перехода из состояния 1 в состояние 2 (то есть от вида кривой р = р(V).
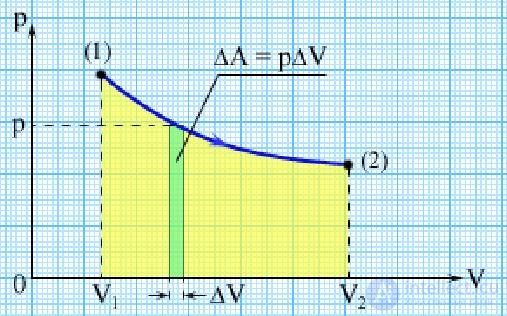
Рис. 2.2. Работа, совершаемая газом
Поэтому работа не является функцией состояния системы.
Рассмотрим теперь процесс передачи теплоты системе.
|
Количество теплоты (теплота) Q — это количественная мера энергии хаотического движения молекул, переданной от одной системы к другой. |
|
Теплообмен — это процесс обмена энергией, который не связан с перемещением макроскопических тел или их частей. |
Изучение тепловых явлений показывает, что теплообмен между телами может осуществляться тремя способами:

Рис. 2.3. Теплообмен путем теплопроводности
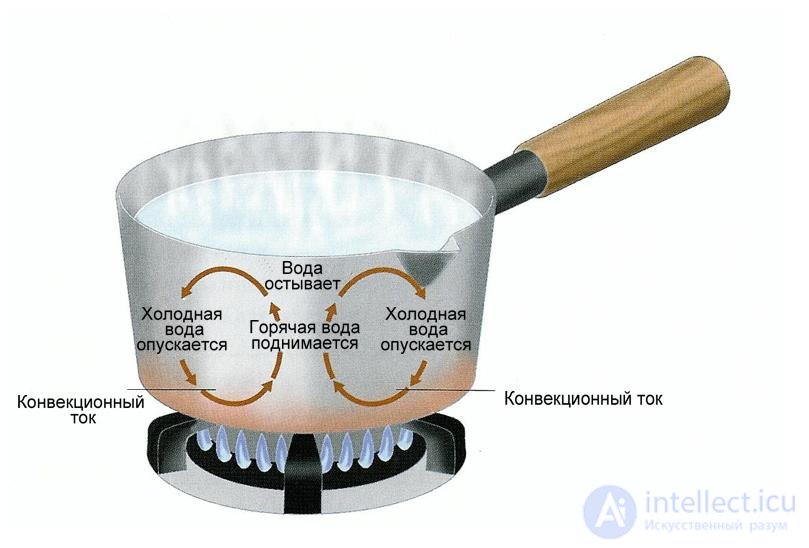
Рис. 2.4. Теплообмен путем конвекции

Рис. 2.5. Теплообмен путем излучения
Тепло, полученное системой, считается положительным, а отданное ею — отрицательным. Поскольку количество теплоты, переданное при теплообмене, связано с изменением энергии движения молекул системы, то о хаотическом беспорядочном движении молекул часто говорят как о тепловом движении.
Будучи одной из форм энергии, теплота измеряется в джоулях (Дж). Но прежде чем была понята связь теплоты и энергии, теплоту измеряли в специальных единицах - калориях. Сообщение одной калории одному грамму воды поднимает ее температуру на один градус Цельсия. Сейчас калория определяется соотношением
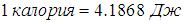
Калория все еще применяется в некоторых областях человеческой деятельности. Вспомните, например, калорийность продуктов питания, в которых многие стараются себя ограничить. При окислении 100 г животных жиров освобождается около 1 000 ккал энергии (для других продуктов поменьше: хлеб — 214 ккал, сыр — 313 ккал, сахар — 390 ккал, шоколад — 428 ккал, масло — 734 ккал).
Пример. Человек массой 90 кг, желающий похудеть, ежедневно 10 раз взбегает по лестнице на 12-й этаж (расстояние между этажами порядка 3 м). Определим, какой вес он потеряет за неделю, если его диета не меняется.
Оценим прежде всего совершаемую за семь дней работу:
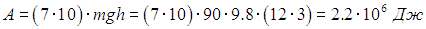
Переведем эту работу в калории:
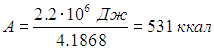
Это соответствует потере приблизительно 50 г массы тела.
Дополнительная информация:
http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 151–158, часть 2, §§3, 4: описаны эксперименты Джоуля по определению механического эквивалента тепла;
Первое начало термодинамики — это закон сохранения и превращения энергии, примененный к тепловым явлениям (рис. 2.6).
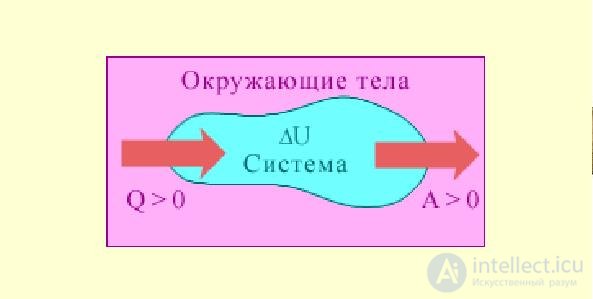
Рис. 2.6. Первое начало термодинамики
|
При получении системой тепловой энергии dQ часть ее тратится на совершение работы dА, а остаток расходуется на изменение внутренней энергии dU системы
|
При конечных изменениях параметров системы имеем
|
|
|
(2.5) |
Как мы видели, внутренняя энергия является функцией состояния системы, а работа зависит от процесса перехода системы из начального состояния в конечное. Отсюда следует, что и теплота не есть функция состояния системы, она тоже зависит от особенностей рассматриваемого процесса. Именно поэтому мы использовали символы dА и dQ для элементарных приращений этих величин: в варианте написания dA, dQ могло бы создаться ложное впечатление, что мы имеем дело с дифференциалами функций А, Q, которых на самом деле не существует.
Имея уравнение состояния (1.7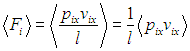 ) идеального газа, мы найдем совершаемую им работу при некоторых типичных процессах. Заодно определим количество теплоты, получаемое от внешнего источника.
) идеального газа, мы найдем совершаемую им работу при некоторых типичных процессах. Заодно определим количество теплоты, получаемое от внешнего источника.
1. Изохорный процесс. При изохорном нагревании или охлаждении (соответственно, прямые 1–2 и 1–3 на рис. 2.7) работа просто равна нулю, поскольку объем не меняется.
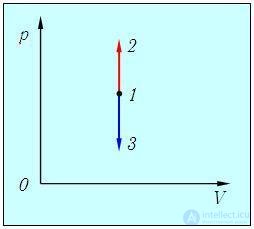
Рис. 2.7. определению работы в изохорном процессе
Получаемое количество теплоты (обозначим Q12 при V = const через Q12V) полностью идет на изменение внутренней энергии газа (см. (1.19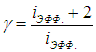 ))
))
|
|
|
(2.6) |
Ту же самую величину можно выразить через изменение температуры газа
|
|
|
(2.7) |
2. Изобарный процесс. Поскольку в этом процессе р = const, то давление можно вынести из-под знака интеграла в (2.3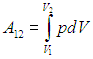 ). Тогда получаем (рис. 2.8)
). Тогда получаем (рис. 2.8)
|
|
|
(2.8) |
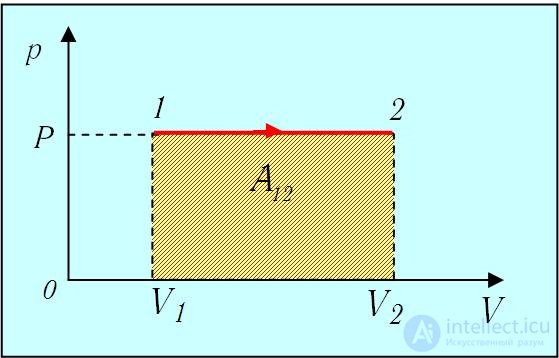
Рис. 2.8. Работа в изобарном процессе
Изменение внутренней энергии газа следует из (1.17) – (1.19)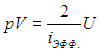
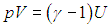
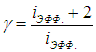 :
:
|
|
|
(2.9) |
Складывая (2.8) и (2.9), находим количество теплоты, переданное газу в этом процессе:
|
|
|
(2.10) |
Пример 1. Пусть система получила при постоянном давлении определенное количество теплоты Q. Найдем, какая часть расходуется на совершение работы А, а какая — на увеличение внутренней энергии газа. Определим также, как зависит ответ от вида используемого газа.
Из формул (2.8) и (2.9) сразу следует, что
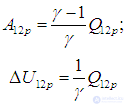
Чем больше g, тем большая часть тепла переходит в работу: для одноатомных газов
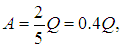
для двухатомных (без учета колебаний ядер, при двух вращательных степенях свободы)
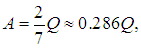
и для многоатомных газов (без учета колебаний ядер, при трех вращательных степенях свободы)
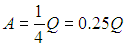
Заметим, что мы излагаем достаточно общий подход, который применим не только к идеальным газам. Для иных систем может измениться уравнение состояния, как следствие изменятся выражения для совершенной работы, но принципы их вывода остаются одними и теми же. Приведем пример. Пусть для некоторой системы давление, температура и объем связаны соотношением
|
|
|
(2.11) |
Найдем выражение для работы такой системы при изменении ее температуры от Т1 до Т2 при постоянном давлении. Поскольку давление постоянно, имеем для работы в изобарном процессе стандартное выражение
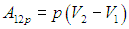
Используя уравнение состояния (2.11), находим отсюда
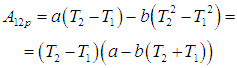
3. Изотермический процесс расширения (или сжатия) газа может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной разности температур. Для этого теплоемкость внешней среды должна быть достаточно велика, и процесс расширения (или сжатия) должен происходить достаточно медленно. Диаграмма изотермического расширения представлена на рис. 2.9.
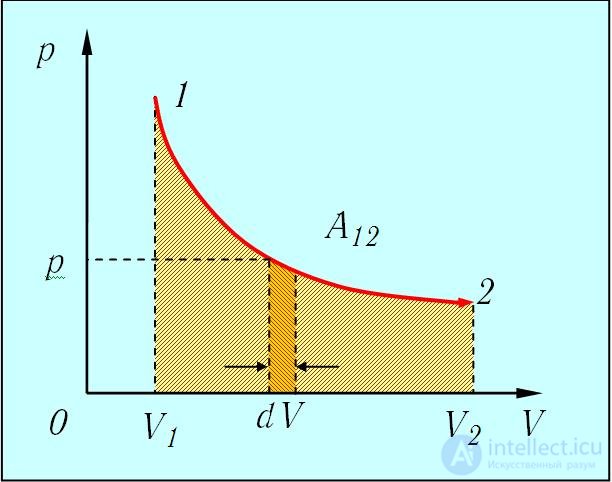
Рис. 2.9. Работа при изотермическом расширении системы
Используя уравнение состояния и выражение (2.2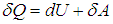 ) для элементарной работы, находим
) для элементарной работы, находим
|
|
|
(2.12) |
Далее используем общее выражение (2.3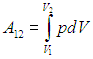 ) для работы при конечном изменении объема
) для работы при конечном изменении объема
|
|
|
(2.13) |
Поскольку объем обратно пропорционален давлению, тот же результат можно представить в виде
|
|
|
(2.14) |
Так как внутренняя энергия идеального газа не меняется при изотермическом процессе, в работу преобразовалась вся теплота, полученная от источника:
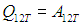
Пример 2. Расширяясь, водород совершил работу 6 кДж. Найдем количество теплоты, подведенное к газу, если процесс протекал: а) изобарно; б) изотермически.
Рассмотрим сначала изобарное расширение. Из формул (2.8) и (2.10) следует связь количества теплоты и совершенной работы:
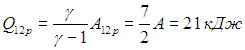
Мы использовали значение g = 7/5 для двухатомного газа. Для изотермического расширения, как мы видели, полученное количество теплоты просто равно произведенной работе:
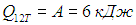
Введем теперь очень важную термодинамическую характеристику, называемую теплоемкостью системы (традиционно обозначается буквой С с различными индексами).
|
Теплоемкость системы — это физическая величина, равная количеству теплоты, которое необходимо передать системе, чтобы увеличить ее температуру на один кельвин (градус):
|
Теплоемкость — величина аддитивная, она зависит от количества вещества в системе. Поэтому вводят также удельную теплоемкость
|
Удельная теплоемкость — это теплоемкость единицы массы вещества
|
и молярную теплоемкость
|
Молярная теплоемкость — это теплоемкость одного моля вещества
|
Поскольку количество теплоты не есть функция состояния и зависит от процесса, теплоемкость также будет зависеть от способа подвода тепла к системе. Чтобы понять это, вспомним первое начало термодинамики. Разделив равенство (2.4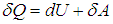 ) на элементарное приращение абсолютной температуры dT, получим соотношение
) на элементарное приращение абсолютной температуры dT, получим соотношение
|
|
|
(2.18) |
Второе слагаемое, как мы убедились, зависит от вида процесса. Отметим, что в общем случае неидеальной системы, взаимодействием частиц которой (молекул, атомов, ионов и т. п.) пренебречь нельзя (см., например, § 2.5 ниже, в котором рассматривается ван–дер–ваальсовский газ), внутренняя энергия зависит не только от температуры, но и от объема системы. Это объясняется тем, что энергия взаимодействия зависит от расстояния между взаимодействующими частицами. При изменении объема системы меняется концентрация частиц, соответственно, меняется среднее расстояние между ними и, как следствие, меняется энергия взаимодействия и вся внутренняя энергия системы. Другими словами, в общем случае неидеальной системы
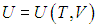 .
.
Поэтому, в общем случае первое слагаемое нельзя писать в виде полной производной, полную производную необходимо заменить на частную производную с дополнительным указанием на то, при какой постоянной величине она вычисляется. Например, для изохорного процесса:
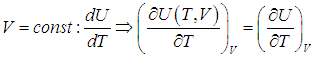 .
.
Или для изобарного процесса
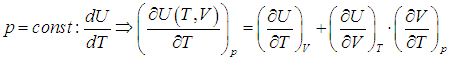
Входящая в это выражение частная производная 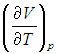 вычисляется с помощью уравнения состояния системы, записанного в виде
вычисляется с помощью уравнения состояния системы, записанного в виде 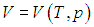 . Об этом говорит сайт https://intellect.icu . Например, в частном случае идеального газа
. Об этом говорит сайт https://intellect.icu . Например, в частном случае идеального газа
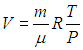 ,
,
эта производная равна
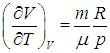 .
.
Мы рассмотрим два частных случая, соответствующих процессу подведения теплоты:
В первом случае работа dА = 0 и мы получаем теплоемкость СV идеального газа при постоянном объеме:
|
|
|
(2.19) |
С учетом сделанной выше оговорки, для неидеальной системы соотношение (2.19) необходимо записать в следующем общем виде
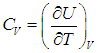
Заменив в 2.7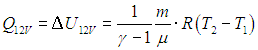
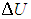 на
на 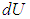 , а
, а 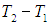 на
на 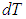 немедленно получаем:
немедленно получаем:
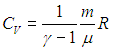 .
.
Для вычисления теплоемкости идеального газа Сp при постоянном давлении (dp = 0) мы учтем, что из уравнения (2.8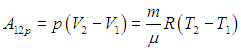 ) следует выражение для элементарной работы при бесконечно малом изменении температуры
) следует выражение для элементарной работы при бесконечно малом изменении температуры
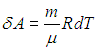
Получаем в итоге
|
|
|
(2.20) |
Разделив это уравнение на число молей вещества в системе, получаем аналогичное соотношение для молярных теплоемкостей при постоянном объеме и давлении, называемое соотношением Майера
|
|
|
(2.21) |
Приведем для справки общую формулу — для произвольной системы — связывающую изохорную и изобарную теплоемкости:

Выражения (2.20) и (2.21) получаются из этой формулы путем подстановки в нее выражения для внутренней энергии идеального газа 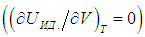 и использования его уравнения состояния (см. выше):
и использования его уравнения состояния (см. выше):
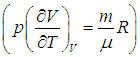 .
.
Теплоемкость данной массы вещества при постоянном давлении больше теплоемкости при постоянном объеме, так как часть подведенной энергии тратится на совершение работы и для такого же нагревания требуется подвести больше теплоты. Отметим, что из (2.21) следует физический смысл газовой постоянной:
|
Газовая постоянная R — это работа, совершаемая молем идеального газа при повышении его температуры на 1 К при постоянном давлении. |
Таким образом, теплоемкость оказывается зависящей не только от рода вещества, но и от условий, в которых происходит процесс изменения температуры.
Как мы видим, изохорная и изобарная теплоемкости идеального газа от температуры газа не зависят, для реальных веществ эти теплоемкости зависят, вообще говоря, также и от самой температуры Т.
Изохорную и изобарную теплоемкости идеального газа можно получить и непосредственно из общего определения, если воспользоваться полученными выше формулами (2.7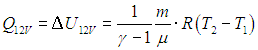 ) и (2.10
) и (2.10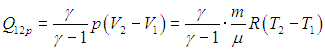 ) для количества теплоты, получаемого идеальным газом при указанных процессах.
) для количества теплоты, получаемого идеальным газом при указанных процессах.
Для изохорного процесса выражение для СV следует из (2.7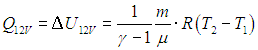 ):
):
|
|
|
(2.22) |
Для изобарного процесса выражение для Ср вытекает из (2.10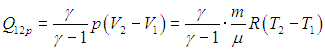 ):
):
|
|
|
(2.23) |
Для молярных теплоемкостей отсюда получаются следующие выражения
|
|
|
(2.24) |
Отношение теплоемкостей равно показателю адиабаты:
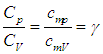
На термодинамическом уровне нельзя предсказать численное значение g; нам удалось это сделать лишь при рассмотрении микроскопических свойств системы (см. выражение (1.19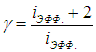 ), а также (1.28
), а также (1.28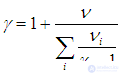 ) для смеси газов). Из формул (1.19
) для смеси газов). Из формул (1.19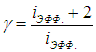 ) и (2.24) следуют теоретические предсказания для молярных теплоемкостей газов и показателя адиабаты.
) и (2.24) следуют теоретические предсказания для молярных теплоемкостей газов и показателя адиабаты.
Одноатомные газы (i = 3):
|
|
|
(2.25) |
Двухатомные газы (i = 5):
|
|
|
(2.26) |
Многоатомные газы (i = 6):
|
|
|
(2.27) |
Экспериментальные данные для различных веществ приведены в таблице 1.
Таблица 1
|
Вещество |
|
|
g |
|
He Ar |
20,97 20,79 |
12,65 12,43 |
1,66 1,67 |
|
H2 O2 N2 CO |
28,77 29,34 29,08 29,33 |
20,42 20,90 20,87 21,12 |
1,41 1,40 1,39 1,39 |
|
CO2 NH3 |
37,23 36,70 |
28,74 27,73 |
1,30 1,32 |
|
Al Cu Ag Au Hg |
24,18 24,47 25,24 25,61 27,68 |
- - - - - |
- - - - - |
Видно, что простая модель идеальных газов в целом неплохо описывает свойства реальных газов. Обращаем внимание, что совпадение было получено без учета колебательных степеней свободы молекул газа.
Мы привели также значения молярной теплоемкости некоторых металлов при комнатной температуре. Если представить кристаллическую решетку металла как упорядоченный набор твердых шариков, соединенных пружинками с соседними шариками, то каждая частица может только колебаться в трех направлениях (iкол = 3), и с каждой такой степенью свободы связаны кинетическая kВТ/2 и такая же потенциальная энергия. Поэтому на частицу кристалла приходится внутренняя (колебательная) энергия kВТ. Умножая на число Авогадро, получим внутреннюю энергию одного моля
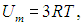
откуда вытекает значение молярной теплоемкости
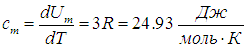
(Вследствие малого коэффициента теплового расширения твердых тел для них не различают ср и cv). Приведенное соотношение для молярной теплоемкости твердых тел называется законом Дюлонга и Пти, и из таблицы видно хорошее совпадение расчетного значения
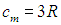
с экспериментом.
Говоря о неплохом соответствии приведенных соотношений и данных опытов, следует отметить, что оно наблюдается лишь в определенном диапазоне температур. Иначе говоря, теплоемкость системы зависит от температуры, и формулы (2.24) имеют ограниченную область применения. Рассмотрим сначала рис. 2.10, на котором изображена экспериментальная зависимость теплоемкости стV газообразного водорода от абсолютной температуры Т.
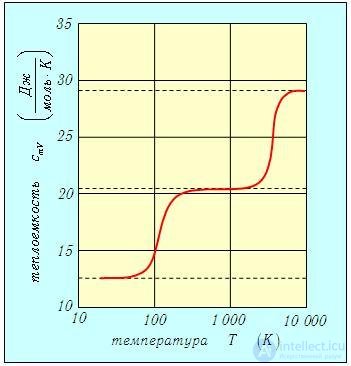
Рис. 2.10. Молярная теплоемкость газообразного водорода Н2 при постоям ном объеме как функция температуры (экспериментальные данные)
Ниже, для краткости, говорится об отсутствии у молекул тех или иных степеней свободы в определенных температурных интервалах. Еще раз напомним, что речь в действительности идет о следующем. По квантовым причинам, относительный вклад во внутреннюю энергию газа отдельных видов движения действительно зависит от температуры и в определенных температурных интервалах может быть мал настолько, что в эксперименте — всегда выполняемом с конечной точностью — он незаметен. Результат эксперимента выглядит так, как будто этих видов движения нет, нет и соответствующих степеней свободы. Число и характер степеней свободы определяются структурой молекулы и трехмерностью нашего пространства — от температуры они зависеть не могут.
Вклад во внутреннюю энергию от температуры зависит и может быть мал.
При температурах ниже 100 К теплоемкость
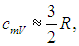
что указывает на отсутствие у молекулы как вращательных, так и колебательных степеней свободы. Далее с ростом температуры теплоемкость быстро возрастает до классического значения
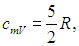
характерного для двухатомной молекулы с жесткой связью, в которой нет колебательных степеней свободы. При температурах свыше 2 000 К теплоемкость обнаруживает новый скачок до значения
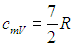
Этот результат свидетельствует о появлении еще и колебательных степеней свободы. Но все это пока выглядит необъяснимым. Почему молекула не может вращаться при низких температурах? И почему колебания в молекуле возникают лишь при очень высоких температурах? В предыдущей главе дано краткое качественное рассмотрение квантовых причин подобного поведения. А сейчас можно лишь повторить, что все дело сводится к специфически квантовым явлениям, не объяснимым с позиций классической физики. Эти явления подробно рассмотрены в последующих разделах курса.
Дополнительная информация
http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 236 — таблица характеристических температур «включения» колебательных и вращательных степеней свободы молекул для некоторых конкретных газов;
Обратимся теперь к рис. 2.11, представляющему зависимость молярных теплоемкостей трех химических элементов (кристаллов) от температуры. При высоких температурах все три кривые стремятся к одному и тому же значению
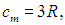
соответствующему закону Дюлонга и Пти. Свинец (Рb) и железо (Fe) практически имеют это предельное значение теплоемкости уже при комнатной температуре.
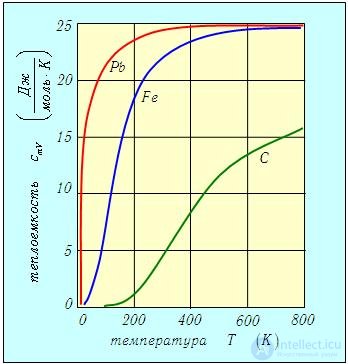
Рис. 2.11. Зависимость молярной теплоемкости для трех химических элементов - кристаллов свинца, железа и углерода (алмаза) — от температуры
Для алмаза же (С) такая температура еще не достаточно высока. А при низких температурах все три кривые демонстрируют значительное отклонение от закона Дюлонга и Пти. Это еще одно проявление квантовых свойств материи. Классическая физика оказывается бессильной объяснить многие наблюдаемые при низких температурах закономерности.
|
Адиабатный процесс — это процесс, при котором не происходит теплообмена с внешней средой. |
Физически это означает, что процесс протекает достаточно быстро и система не успевает обменяться теплотой с внешними телами. Однако коль скоро мы имеем дело с равновесными процессами, скорость адиабатного процесса не должна быть слишком уж велика. Примером таких процессов может служить распространение звуковых колебаний в упругой среде.
Выведем уравнение, описывающее адиабатный процесс. Ранее мы имели дело с самыми простыми уравнениями процессов
|
|
— для изотермического процесса; |
|
|
— для изобарного процесса; |
|
|
— для изохорного процесса. |
Поскольку в адиабатном процессе dQ = 0, из первого начала термодинамики следует, что
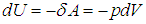
C другой стороны,
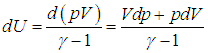
Приравнивая эти выражения, находим
|
|
|
(2.28) |
Умножая уравнение (2.28) на Vg–1, получаем в левой части полный дифференциал
|
|
|
(2.29) |
В результате интегрирования (2.29) приходим к уравнению адиабатного процесса
|
|
|
(2.30) |
Графически адиабатный процесс описывается на (р,V) — диаграмме кривыми, похожими на изотермы (рис. 2.12), но идущими круче, так как g > 1, поскольку Сp > СV.
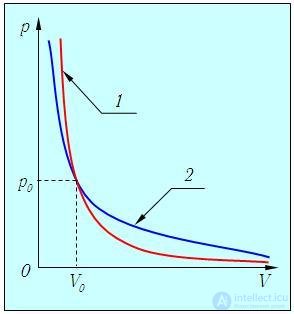
Рис. 2.12. Адиабатный процесс в идеальном газе: 1 — адиабата, 2 — изотерма
Это и понятно, так как при адиабатном расширении газ совершает работу за счет внутренней энергии, и его температура падает, что еще больше уменьшает давление по сравнению с изотермическим расширением.
Экспериментальное исследование адиабатного процесса в идеальном газе можно выполнить с помощью установки, представленной на рис. 2.13.
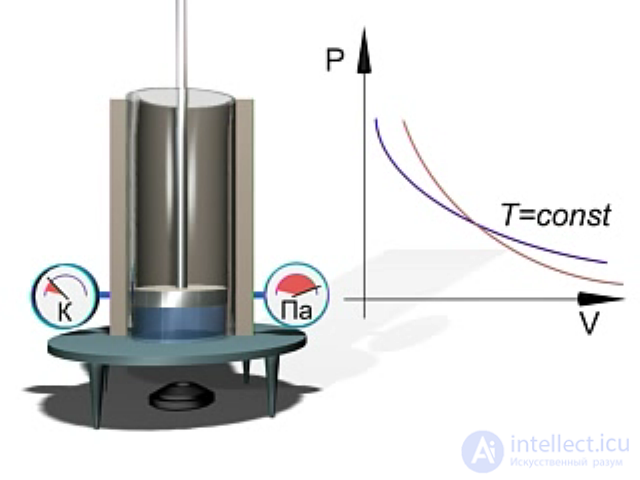
Рис. 2.13. Экспериментальное изучение адиабатного процесса в идеальном газе
Учитывая, что из уравнения состояния идеального газа следует пропорциональность
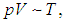
уравнение адиабатного процесса можно также представить в виде
|
|
|
(2.31) |
Первый закон термодинамики в применении к адиабатному процессу позволяет вычислить работу газа при адиабатном расширении:
|
|
|
(2.32) |
Выражения для работы при адиабатном процессе с учетом уравнения Клапейрона — Менделеева можно выразить также через температуры в начале и конце процесса
|
|
|
(2.33) |
Для бесконечно малых изменений параметров уравнения (2.32), (2.33) переходят в соотношения
|
|
|
(2.34) |
Пример. Горючая смесь в двигателе Дизеля (см. рисунок выше) воспламеняется при температуре Т2 = 1 100 К. Начальная температура смеси Т1 = 350 К. Определим, во сколько раз нужно уменьшить объем смеси при сжатии, чтобы она воспламенилась. Сжатие будем считать адиабатным. Показатель адиабаты для смеси g = 1,4.
Для решения удобнее воспользоваться уравнением адиабатного процесса в форме (2.31):
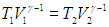
Отсюда сразу следует выражение для степени сжатия горючей смеси:
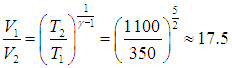
Уравнение Клапейрона — Менделеева следует из молекулярно-кинетической теории в предположении идеальности газа. Если мы хотим описывать поведение реальных систем, надо учесть взаимодействие молекул между собой. Точный учет межмолекулярных сил — задача чрезвычайно трудная. Поэтому было предложено несколько модификаций уравнения состояния идеального газа, которые могли бы учесть основные особенности реальных систем. Наиболее удачной попыткой стало уравнение Ван-дер-Ваальса, при получении которого вносились поправки в уравнение состояния идеального газа
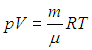
В подходе Ван-дер-Ваальса, во-первых, принимается во внимание, что молекулы имеют конечные размеры. Если обозначить собственный объем всех молекул в моле вещества буквой b, то для движения молекул остается свободный объем
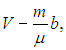
и именно он должен фигурировать в уравнении состояния. Во-вторых, учитывается, что молекула, подлетающая к стенке сосуда, «чувствует» притяжение других молекул, которое уравновешивалось, когда молекула была внутри сосуда. Дополнительная сила, направленная внутрь сосуда, эквивалентна дополнительному давлению pi, (его называют «внутренним» давлением газа). Поэтому вместо давления р газа на стенки сосуда уравнение состояния должно содержать сумму р+рi.
Как зависит внутреннее давление pi от параметров системы? Сила, действующая на каждую молекулу, пропорциональна концентрации п молекул в системе. Число подлетающих к стенке молекул также пропорционально п, и потому внутреннее давление пропорционально квадрату концентрации частиц:
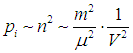
Обозначая коэффициент пропорциональности буквой а, приходим к уравнению Ван-дер-Ваальса
|
|
|
(2.35) |
Для одного моля вещества это уравнение упрощается:
|
|
|
(2.36) |
Дополнительная информация
http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 38–47, ч. I, § 6, п.п. б, в. — обсуждается уравнение Ван-дер-Ваальса и приводятся экспериментально полученные межмолекулярные потенциальные энергии взаимодействия для гелия, водорода, аргона и углекислого газа;
http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 246–248 — детальная информация о силах межмолекулярного притяжения в газе Ван-дер-Ваальса.
Рассмотрим вид изотерм газа Ван-дер-Ваальса на (р,V) - диаграмме (рис. 2.14). Они описываются функцией
|
|
|
(2.37) |
При достаточно высоких температурах и больших объемах введенными поправками можно пренебречь, и вид изотерм получится обычным. При понижении температуры вид изотерм все более искажается и при некотором критическом значении температуры Тс данная изотерма приобретает точку перегиба (критическую точку) с координатами (рс, Vc), в которой равны нулю первая и вторая производные давления по объему. При дальнейшем понижении температуры точка перегиба превращается в минимум и максимум функции p(V).
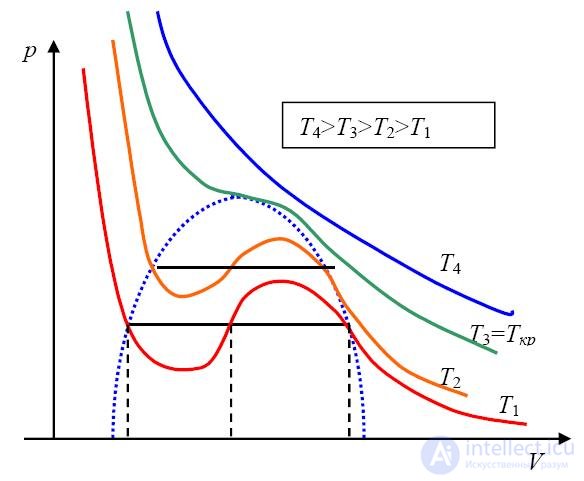
Рис. 2.14. Изотермы газа Ван-дер-Ваальса
Найдем сначала значения параметров, соответствующих критической точке. Берем первую и вторую производные функции (2.37) и приравниваем их нулю:
|
|
|
(2.38) |
Решение этой пары уравнений даст нам критические значения Tc и Vc. Находя из первого уравнения значение
|
|
|
(2.39) |
подставляем его во второе уравнение, откуда тогда следует
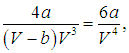
или
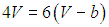
Получаем сначала значение молярного критического объема
|
|
|
(2.40) |
Подставляя его в уравнение (2.39), находим критическую температуру
|
|
|
(2.41) |
Наконец, подставляя найденные значения Тс, Vc в уравнение (2.37), находим критическое давление
|
|
|
(2.42) |
Эти критические значения получены для одного моля вещества. Чтобы найти их для произвольного числа молей, заметим, что при переходе от уравнения (2.36) к (2.35) надо произвести масштабное преобразование
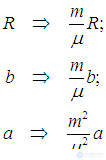
Выполняя то же преобразование в формулах для критических значений термодинамических параметров, убеждаемся, что критические температура и давление не изменяются, а объем преобразуется естественным образом:
|
|
|
(2.43) |
Значения критических параметров берутся из данных эксперимента. Отметим, что газовая постоянная R также может быть выражена через критические параметры:
|
|
|
(2.44) |
Для каждого реального газа следует вычислять свою индивидуальную газовую постоянную R, которая будет отличаться от универсальной газовой постоянной NAkB идеального газа. Этому не следует удивляться, учитывая феноменологический приближенный характер уравнения Ван-дер-Ваальса. Значения критических параметров некоторых веществ и их газовая постоянная приведены в табл. 2.
Таблица 2.
Критические параметры некоторых газов
|
Газ |
Тс , К |
рс , МПа |
Vm , см3/моль
|
|
|
Не |
5.2 |
0.23 |
57.5 |
0.82 |
|
Н2 |
33.2 |
1.30 |
65.5 |
0.82 |
|
02 |
154.8 |
5.08 |
78 |
0.82 |
|
С02 |
304.1 |
7.39 |
94 |
0.73 |
|
Н20 |
647.3 |
22.1 |
56.3 |
0.62 |
Возьмем для примера пары воды. Из таблицы следует значение коэффициента
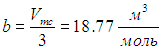
Поделив на число Авогадро, получаем объем одной молекулы
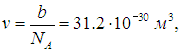
откуда для диаметра молекулы следует оценка
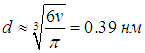
Это действительно близко к размерам молекулы воды, что свидетельствует о правильности модели Ван-дер-Ваальса.
Введем обозначения в виде соответствующих греческих букв для термодинамических параметров, измеренных в единицах их критических значений, то есть для безразмерных отношений:
|
|
|
(2.45) |
В этих обозначениях все критические значения термодинамических параметров равны единице, а уравнение Ван-дер-Ваальса (2.36) принимает простой вид
|
|
|
(2.46) |
Отметим универсальность этого уравнения, которое может быть использовано даже без точного знания значений критических параметров (но они нужны, конечно, при возвращении к обычным единицам измерения температуры, давления и объема).
На рис. 2.15 представлены изотермы газа Ван-дер-Ваальса для нескольких значений температуры (q=2; 1.1; 1; 0.9; 0.85).
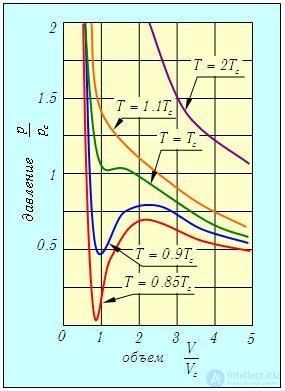
Рис. 2.15. Изотермы газа Ван-дер-Ваальса для различных значений температуры (построены для безразмерных отношений термодинамических параметров р, V , Т к их критическим значениям рс , Vc , Tc)
При достаточно высоких температурах Т = 2Тс (q = 2) изотермы Ван-дер-Ваальса совпадают с изотермами идеального газа за исключением области малых объемов. При понижении температуры гиперболы начинают искажаться и при Т = Тс (q = 1) график имеет точку перегиба при р = рс , V = Vc (p = 1, u = 1). При еще более низких температурах на изотерме появляются минимум и максимум.
Теоретическая изотерма Ван-дер-Ваальса отличается от экспериментальной. Иначе и быть не может, так как область между минимумом и максимумом описывает нестабильное состояние системы, которое не может быть реализовано. В этой области давление растет при увеличении объема и падает при уменьшении. Представим себе какое-нибудь состояние в этой области (точку на растущей ветви графика). Если в результате флуктуации внешняя сила, удерживающая газ в некотором объеме, несколько возрастет, то объем газа слегка уменьшится, и это, в отличие от обычных состояний, приведет к уменьшению давления газа. Испытывая меньшее сопротивление, внешняя сила сильнее сожмет газ, давление его еще уменьшится и т. д. Словом, такое состояние столь же нестабильно, как и равновесие иглы, стоящей на кончике.
Поэтому если газ изотермически сжимать (при Т < Тс), то при некотором значении объема V давление газа перестает меняться. На рисунке 2.16 это соответствует точке 1 на горизонтальном участке изотермы.
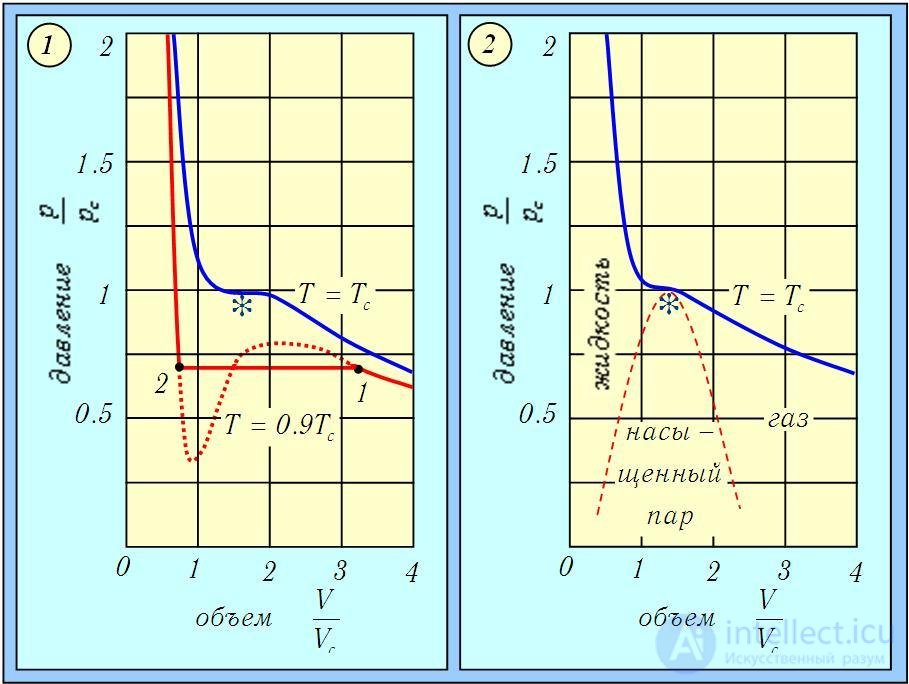
Рис. 2.16. Изотермы Ван-дер-Ваальса: штриховая часть изотермы при Т = 0,9ТС соответствует неустойчивым состояниям газа (1); область насыщенного пара (2) получена соединением концов горизонтальных участков изотерм при различных температурах
На этом участке, происходит конденсация газа в жидкость: над жидкостью образуется насыщенный пар, давление которого рН(T) зависит только от температуры и потому не меняется (рис. 2.17).
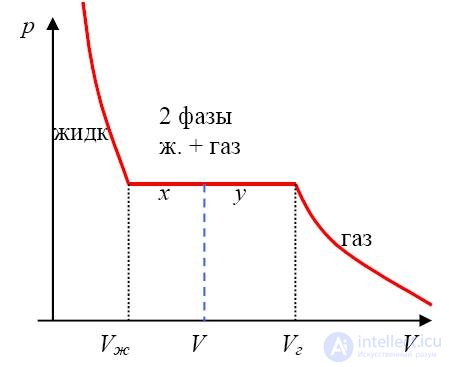
Рис. 2.17. Экспериментальная изотерма реального газа
Покажем, что давление термодинамически равновесной двухфазной системы зависит только от ее температуры, для этого рассмотрим условия термодинамического равновесия в такой системе.
В отсутствие обмена частицами, необходимыми условиями термодинамического равновесия двух тел являются равенства температур и давлений. Равенство температур необходимо для того, чтобы отсутствовал теплообмен между телами. Равенство давлений — для того, чтобы ни одно из этих тел не совершало работу над другим телом. При рассмотрении равновесия двух фаз одного и того же вещества, например, жидкости (жидкая фаза) и ее пара (газовая фаза), необходимо дополнительно учитывать возможность обмена частицами. При испарении молекулы покидают жидкую фазу, переходя в газовую, при конденсации — наоборот: молекулы из газа переходят в жидкость. В состоянии термодинамического равновесия средние скорости этих процессов должны быть равны, тогда обмена частицами — в среднем — не будет. Пусть за время dt из жидкости в пар перешло dNж-п молекул, а из пара в жидкость — dNп-ж молекул. Дополнительным необходимым условием равновесия жидкой и газовой фаз является равенство скоростей испарения 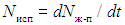 и конденсации
и конденсации 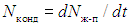 .
.
Таким образом, должно выполняться три условия равновесия двух фаз:
|
|
|
(2.47) |
|
|
|
(2.48) |
|
|
|
(2.49) |
где Тп, Рп, Тж, Рж — температура и давление пара и жидкости; Т и Р — их равновесные значения.
Как отмечено в (2.49), скорости испарения и конденсации в силу ряда причин зависят и от давления, и от температуры соответствующих фаз (Nисп — жидкой, Nконд — газовой). Укажем лишь на некоторые, наиболее очевидные. Чтобы покинуть жидкость, молекула должна преодолеть межмолекулярное притяжение и, следовательно, обладать достаточной для этого кинетической энергией. Чем выше температура жидкости, тем больше таких молекул, и, следовательно, скорость испарения. Для перехода из газа в жидкость молекула должна по крайней мере подлететь к поверхности жидкости. Следовательно, скорость конденсации пропорциональна потоку молекул, т. е. µ n < v >, здесь n — концентрация молекул, а < v > — их средняя скорость Чем выше давление газа, тем (при Т = const) выше n и, соответственно, Nконд; чем выше температура газа, тем больше µ T1/2 и (при n = const) Nконд.
Заменив в (2.49) давления и температуры фаз на их равновесные значения Р и Т из (2.47) и (2.48), получаем уравнение:
|
|
|
(2.50) |
связывающее давление насыщенного пара Р с температурой системы Т:
|
|
|
(2.51) |
Таким образом, давление насыщенного пара зависит только от температуры системы «жидкость — пар». Соответствующая зависимости (2.51) кривая на плоскости (Р, Т) называется кривой испарения.
Совершенно аналогично можно показать, что давление в двухфазной системе кристалл – жидкость или в системе кристалл — газ также зависит только от температуры этой системы. Отличие состоит только в том, что вместо условия равенства скоростей испарения и конденсации (2.49) необходимо рассмотреть условие равенства скоростей плавления и кристаллизации в первом случае и скоростей сублимации и обратного процесса перехода из газовой фазы в кристаллическую ˗ во втором случае.
Вернемся к рассмотрению системы жидкость – пар.
При дальнейшем уменьшении объема газа (сжатии) все большая его часть переходит в жидкое состояние. Наконец, при значении объема, соответствующем точке 2, весь газ переходит в жидкость, горизонтальный участок изотермы заканчивается и давление резко возрастает. Если построить такие горизонтальные участки изотерм для разных температур Т < Тс , то они заполнят область, граница которой показана штрихпунктирной линией на рисунке 1-2. Эта область (насыщенный пар) соответствует сосуществованию жидкой и газообразной фаз, справа от нее лежит область газообразной фазы, слева — жидкой.
При критической температуре Т = Тс горизонтальный участок изотермы стягивается в точку (показана звездочкой на рис. 1), называемую критической точкой.
Рассматривая рисунки, можно прийти к следующим выводам:
Видео 2.2. Критическое состояние эфира.
Пример 1. Найдем наибольший объем V, который может занимать вода массой 1 кг.
Как было сказано, из вида изотерм Ван-дер-Ваальса на рис. 2.9 следует, что наибольший объем данная масса жидкости может занимать в критической точке. Поэтому используем (2.44):
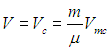
Значение Vmc берем из таблицы 2, откуда следует
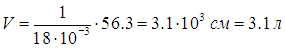
— в три раза больше объема воды в обычных условиях!
Заметим, что зависимость давления насыщенного пара от температуры рН(Т) проявляется, в частности, в изменении температуры кипения воды при подъеме в горы. Точка кипения определяется из равенства давления насыщенного пара атмосферному давлению. Понижение последнего приводит к более низкой изотерме на нашем рисунке, то есть. к понижению температуры кипения.
Напомним заодно, что вместе с атмосферным давлением и температурой воздуха в сводках погоды сообщают и его относительную влажность. Под ней понимается выраженное в процентах отношение парциального давления водяного пара, содержащегося в воздухе, к давлению насыщенного пара при данной температуре. Таким образом, 100 % влажность вовсе не означает, что вместо воздуха мы стали дышать водой. Давление насыщенного водяного пара при некоторых значениях температуры приведено в табл.
Давление насыщенных паров воды
|
t °С |
рН, кПа |
t °С |
рН, кПа |
t °С |
рН, кПа |
t °С |
рН, МПа |
|
0 |
0,61 |
25 |
3,17 |
60 |
19,9 |
200 |
2,32 |
|
5 |
0,87 |
30 |
4,24 |
70 |
31,2 |
250 |
3,98 |
|
10 |
1,23 |
35 |
5,63 |
80 |
47,4 |
300 |
8,59 |
|
15 |
1,71 |
40 |
7,37 |
90 |
70,1 |
350 |
16,5 |
|
20 |
2,34 |
50 |
12,3 |
100 |
101 |
374 |
22,1 |
Пример 2. По радио передали, что атмосферное давление равно р = 757 мм ртутного столба (плотность ртути ρ = 3,55 г/м3), относительная влажность воздуха r = 86 %, а температура воздуха 20 °С. Найдем абсолютную влажность воздуха rа (то есть массу водяных паров в единице объема), а также определим, какую долю h от атмосферного давления составляет парциальное давление водяных паров.
Сначала определим значение атмосферного давления в единицах СИ. Давление ртутного столба высотой h равно
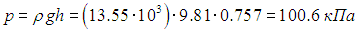
По табл. 3 находим давление насыщенных паров при данной температуре воздуха: рН = 2,34 кПа. Парциальное давление паров воды
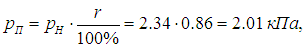
и мы можем уже ответить на второй вопрос задачи:
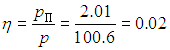
Поскольку искомая абсолютная влажность есть не что иное, как плотность водяного пара
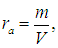
применяя уравнение Клапейрона — Менделеева для водяного пара, немедленно находим
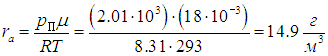
Пример 3. Если температура в предыдущем примере понизится, то в воздухе может появиться туман. Определим, при какой температуре это произойдет. Найдем также, какое количество росы выпадет на землю при понижении температуры до 10 °С.
Видео 2.3. «Генератор» тумана: теплая вода и жидкий азот.
Надо найти температуру tp (ее называют точкой росы), при которой давление рН насыщенного водяного пара станет равным полученному выше парциальному давлению паров воды рП = 2,01 кПа. Тогда относительная влажность воздуха достигнет 100 %, и дальнейшее понижение температуры приведет к конденсации «излишков» пара. В табл. нет значения 2,01 кПа для давления насыщенного пара, но можно утверждать, что искомая температура находится в интервале от 15 °С до 20 °С. Поскольку он не столь велик, для более точного определения точки росы используем линейное приближение: будем считать, что в указанном интервале зависимость давления от температуры является линейной:
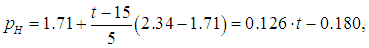
где давление измеряется в кПа, а температура — в градусах Цельсия. Приравнивая рН и рП, находим точку росы
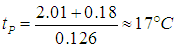
При понижении температуры до значения t1=10 °С давление насыщенного пара понижается до рH1 = 1,23 кПа, как следует из той же таблицы, то есть становится меньше прежнего рН = 2,01 кПа. В этой же пропорции уменьшается плотность водяных паров:
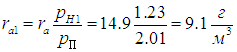
Следовательно, из каждого кубометра воздуха на землю выпадет
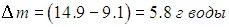
Дополнительная информация
http://kvant.mirror1.mccme.ru/ — Журнал Квант, 2004, № 2, стр. 23–25, В. Можаев «Насыщенные и ненасыщенные водяные пары» — решается несколько интересных задач, касающихся испарения воды;
http://www.alleng.ru/d/phys/phys62.htm — Тульчинский М.Е. Качественные задачи по физике, Изд. Просвещение, 1972 г.; задача № 611 на насыщенные пары;
http://kvant.mirror1.mccme.ru/1996/05/otkuda_berutsya_oblaka.htm — Журнал Квант, 1996 г. № 5, стр.40–41, А. Айзенкрафт, Л. Кирпатрик, Откуда берутся облака?
http://experiment.edu.ru/catalog.asp?cat_ob_no=12329&ob_no=12384 — Демонстрация кипения жидкости при пониженном давлении;
http://experiment.edu.ru/catalog.asp?cat_ob_no=12329&ob_no=12390 — Демонстрация опыта по расширению воды при замерзании;
http://by-chgu.ru/category/physics — Физическая энциклопедия, т. 1, М., 1988, стр.278–279 — описано использование пересыщенного пара для регистрации электрически заряженных частиц в камере Вильсона;
http://by-chgu.ru/category/physics — Физическая энциклопедия, т. 4, М., 1994, стр. 177–179 — описано использование перегретой жидкости для регистрации электрически заряженных частиц.
Видео 2.4. Перегретая жидкость: добавление центров парообразования приводит к вскипанию перегретой жидкости.
Наличие «внутреннего» давления
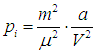
газа Ван-дер-Ваальса приводит к тому, что внутренняя энергия такого газа по сравнению с внутренней энергией идеального газа Uид включает добавку — потенциальную энергию взаимодействия молекул между собой. Эта дополнительная потенциальная энергия получается равной
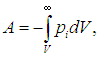
где знак «минус» означает притяжение между молекулами. Тогда для внутренней энергии газа Ван-дер-Ваальса имеем соотношение
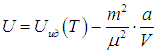
Данная формула отражает тот факт, что при увеличении объема газа производится работа против сил притяжения между молекулами. Из нее следует теоретическое объяснение эффекта Джоуля — Томсона (рис. 2.18).
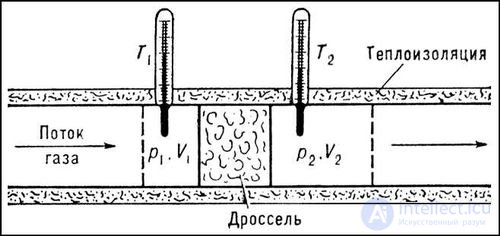
Рис. 2.18. Эффект Джоуля — Томсона
В этом эффекте газ адиабатно расширяется в пустоту. Поскольку нет подвода тепла и газ не совершает работы против внешнего давления, его внутренняя энергия U должна оставаться постоянной. Для идеального газа это эквивалентно постоянству температуры. Но для газа Ван-дер-Ваальса уменьшение вычитаемого в выражении для внутренней энергии при U = const влечет за собой уменьшение первого члена, то есть понижение температуры. Этим эффектом пользуются при сжижении газов. В веществах, где доминирует отталкивание между молекулами, добавка к U положительна, и наблюдается повышение температуры при адиабатном расширении, то есть обратный эффект Джоуля — Томсона.
Исследование, описанное в статье про термодинамика, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое термодинамика, теплоемкость системы, адиабатный процесс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Молекулярная физика и термодинамика
Комментарии
Оставить комментарий
Молекулярная физика и термодинамика
Термины: Молекулярная физика и термодинамика