Лекция
Привет, Вы узнаете о том , что такое 3. Распределение молекул по скоростям и координатам, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3. Распределение молекул по скоростям и координатам , настоятельно рекомендую прочитать все из категории Молекулярная физика и термодинамика.
Предположение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют предположением о молекулярном хаосе. Как ни странно это выглядит, именно благодаря абсолютной хаотичности движения молекул можно установить определенные закономерности, которым подчиняется состояние системы. Кроме того, на практике часто приходится иметь дело с газом, находящимся в однородном внешнем поле сил, наиболее важным примером которого является поле силы тяжести.
Пусть имеется некоторый замкнутый сосуд небольшого (чтобы пренебречь действием внешних силовых полей) объема, заполненный газом. Предположим, что в газе установилось состояние равновесия.
|
Равновесное состояние системы — это такое состояние, при котором все параметры системы имеют определенные значения, остающиеся постоянными сколь угодно долго при неизменных внешних условиях. |
Внешние условия должны быть такими, чтобы в системе не было переноса вещества, энергии, импульса и т. п.
Видео 3.1. Флуктуации числа молекул в половине сосуда вполне заметны, если число молекул невелико.
Опыт показывает, что при равновесии, в отсутствие внешних силовых полей:
|
|
|
(3.1) |
Видео 3.2. Хаотичность движения молекул приводит к равномерному их распределению по всему объему сосуда. При большом числе молекул флуктуации их числа в половине сосуда малосущественны.
Это означает, что число молекул, движущихся в любом направлении, должно быть одинаковым. Если бы это было не так и существовало бы направление преимущественного движения молекул, то в этом направлении возник бы поток газа, что противоречит предположению о наличии равновесия.
В пределах любым образом ориентированных, но одинаковых по величине телесных углов лежат направления движения в среднем одинакового числа молекул (рис. 3.1).

Рис. 3.1. Распределение молекул по направлениям движения
Соударения молекул не изменяют эту ситуацию. Для простоты мы будем рассматривать идеальный газ. С точки зрения кинетической теории, идеальный газ — простейшая молекулярно-кинетическая модель газа.
Модель идеального газа, как отмечалось ранее, предполагает следующие два свойства:
Реальные газы близки к идеальному газу при малых плотностях. При уменьшении плотности средние расстояния между молекулами значительно превосходят линейные размеры молекул, и сила взаимодействия друг с другом уменьшается практически до нуля.
Функция распределения. Что такое распределение? Начнем с простого примера, позволяющего сформулировать необходимые определения. Пусть в некотором коллективе из 100 человек 10 имеют рост от 160 до 165 см, 25 - от 165 до 170, 35 — от 170 до 175, 15 — от 175 до 180, 10 — от 180 до 185 и остальные 5 — от 185 до 190. Это перечисление удобно изобразить в виде простой общепринятой диаграммы, рисуя вертикальные прямоугольники с высотой, пропорциональной числу людей данного роста (рис. 3.2). Такую диаграмму называют гистограммой. Если построить ее не для ста человек, а для взрослого населения целой страны, то можно ввести гораздо более мелкие подразделения по росту. Например, определять рост с точностью не 5 см, а 0,5 см (применительно к росту человека большая точность вряд ли имеет смысл).
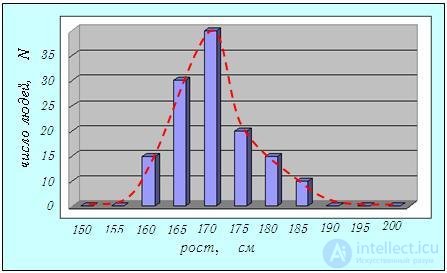
Рис. 3.2. Гистограмма, изображающая распределение людей по росту, и примерный вид соответствующей функции распределения (штриховая кривая)
Видео 3.3. Случайными могут быть столкновения не только молекул газа между собой: «генерация» распределения Гаусса с помощью зерен пшена.
Допустим, однако, что некоторая изучаемая величина может задаваться сколь угодно точно, так что для весьма большого коллектива законно перейти от гистограммы к плавной функции распределения, график которой проходит через середины верхних сторон вертикальных прямоугольников гистограммы (штриховая кривая на рис. 3.2). Кривую такого рода мы и должны построить для распределения молекул газа по скоростям.
Случайные события. Раздел математики, изучающий случайные явления, называется теорией вероятностей. Ее основой является понятие случайного события как одного из возможных исходов некоторого испытания — процесса, который принципиально может воспроизводиться неограниченное число раз. На интуитивном уровне это понятие ясно, и мы не станем вдаваться в его формальное определение, принятое в современной математике. Выпадение числа 6 (или любого другого) при бросании игральной кости, появление красного или черного в игре в рулетку — примеры случайных событий.
Зачастую, однако, мы имеем дело с невоспроизводимыми событиями, к которым все же применима теория вероятности. Речь идет о количественных характеристиках массовых явлений. Скажем, на предприятии изготавливается транзистор. Он может быть дефектным или исправным, но в отличие от бросания игральной кости повторить процесс, изготовить тот же самый транзистор во второй, третий, ..., миллионный раз уже невозможно. К этому же классу явлений относится появление данного числа вызовов на телефонной станции, возраст человека, занимающего определенное место на стотысячном стадионе, и т. п.
Можно ли случайные события или массовые явления описывать математическими формулами? Можно ли в мире случайностей найти некоторые закономерности? Такие попытки предпринимались издавна из-за потребностей практики. Еще в древних государствах делались прогнозы роста народонаселения и количества собираемого урожая и податей. Развитие страхового дела в средние века потребовало оценки степени опасности кораблекрушения. В XVII в. в Италии было основано первое общество по страхованию жизни, и его основателю надо было знать степень риска смерти клиента в зависимости от его возраста и профессии. Последним толчком к появлению теории вероятностей как самостоятельной математической дисциплины стало распространение азартных игр.
Вероятность случайного события. Каждому случайному событию можно приписать число, которое называется вероятностью события. Вероятность некоторого случайного события определяется относительной частотой его появления в ряду других случайных событий. Чем чаще происходит событие, тем больше его вероятность.
Пусть производится некоторое испытание, исходом которого является какой-то набор случайных событий А, В, С, .... Скажем, бросается игральная кость, которая предполагается геометрически правильной, так что все ее грани равноправны. Возможно всего шесть событий - выпадение чисел 1, 2, ..., 6. Пусть произведено n испытаний, и событие А наступило kn(А) раз. Величина
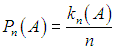
представляет собой относительную частоту события А в данной серии испытаний. Вообще говоря, значение Pn(А) колеблется при переходе от одной серии испытаний к другой. Если при увеличении числа n испытаний в серии число Pn(А) стремится к определенному пределу
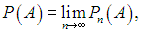
то этот предел Р(А) называется вероятностью события А. Если кость бросается достаточно много раз в нашем примере, то частота выпадения каждого из чисел будет одинаковой. Мы скажем, что вероятность выпадения любого из них равна 1/6.
Из классического определения вероятности следует, что она всегда заключена между нулем и единицей:
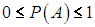
|
Вероятность невозможного события равна нулю, вероятность достоверного события равна единице. |
Обратные утверждения, вообще говоря, неверны. Например, не следует думать, что никогда не может осуществиться событие, вероятность которого равна нулю. События, которые осуществляются при бросании кости, дискретны: возможно выпадение единицы или двойки, но не двух с половиной. Но что делать, если события будут непрерывными? Например, вернемся к примеру группы людей. Какова вероятность того, что рост наудачу выбранного индивидуума будет в точности равен 176,543... см? Ясно, что эта вероятность равна нулю: существует бесчисленное множество непрерывно распределенных значений роста (возможных исходов измерений), так что знаменатель нашего определения вероятности бесконечно велик. Но все же может случиться так, что какой-то индивидуум имеет в точности такой рост. Чтобы избежать подобных трудностей, в таких случаях вместо вероятности события удобнее пользоваться плотностью вероятности, или, что то же самое, функцией распределения. Зная эту функцию, мы сможем, например, ответить на такой вопрос: какова вероятность того, что рост этого индивидуума заключен между 175 см и 180 см? В нашем примере эта вероятность составляет
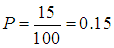
Та плавная кривая, которая соответствует гистограмме на рис. 3.2, при уменьшении интервала измерений роста приближается как раз к плотности вероятности.
Закон сложения вероятностей.
|
Два события А и В называются несовместимыми, если при проведении испытания они не могут произойти одновременно. |
|
Суммой, (или объединением) событий A и В называется наступление одного из них. |
Вероятность наступления одного из двух несовместимых событий А или В определяется законом сложения вероятностей:
|
|
|
(3.2) |
Обобщение закона (3.2) на произвольное число несовместимых событий очевидно.
Пример 1. Какова вероятность, что при однократном бросании кости выпадет четное число?
Поскольку выпадение какого-то из чисел исключает выпадение другого, то эти события несовместимы. На гранях кости имеются четные числа 2, 4, 6, вероятности появления которых одинаковы:
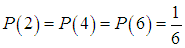
Вероятность выпадения четного числа
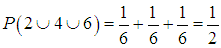
Очевидность полученного результата иллюстрирует высказывание французского математика Лапласа, что теория вероятностей есть здравый смысл, сведенный к математическому исчислению.
Рассмотрим вновь коллектив из ста человек. Здесь мы имеем дело с вероятностями того, что рост индивидуума заключен в определенных пределах. Так, мы знаем вероятность того, что рост находится в пределах от 175 см до 180 см равна 0,15, вероятность того, что рост находится в пределах от 180 см до 185 см равна 0,10, а вероятность того, что рост находится в пределах от 185 см до 190 см равна 0,05. Какова вероятность того, что рост наугад выбранного человека из этого же коллектива превышает 175 см? По закону сложения вероятности приходим к ответу

Аналогично находится вероятность того, что рост будет ниже 175 см:
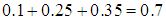
Зададим теперь вопрос: чему равна вероятность того, что произвольно выбранный индивидуум имеет какой-нибудь рост? Вероятность эта равна единице:
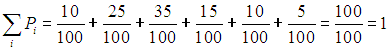
что согласуется с определением вероятности. Мы рассмотрели пример условия нормировки вероятности.
Итак, события, исходы которых принимают непрерывный ряд значений, описываются непрерывной функцией распределения. Для нашего примера с распределением ростов в большом коллективе функцию распределения обозначим w(h). Тогда бесконечно малая величина w(h)dh равна вероятности того, что рост индивидуума заключен в пределах от h до h + dh. Чтобы узнать вероятность P(h1, h2), что индивидуум имеет рост в пределах
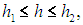
надо просуммировать все эти бесконечно малые величины, то есть вычислить площадь под частью кривой w(h) между точками с координатами h1 и h2:
|
|
|
(3.3) |
Интеграл от функции распределения по всей области ее определения должен быть равен единице, поскольку сумма всех возможных событий является достоверным событием.
Закон умножения вероятностей.
|
Произведением, (или пересечением), событий А и В называется одновременное осуществление обоих из них. |
|
Два события называются независимыми, если наступление одного из них не влияет на вероятность наступления другого. |
Для двух независимых событий выполняется закон умножение вероятностей:
|
|
|
(3.4) |
Пример 2. Пусть бросаются две игральные кости. Какова вероятность, что сумма чисел на гранях равна 12?
Такой исход возможен при выпадении шестерок на каждой из костей, причем число очков на одной из костей с очевидностью не влияет на число очков на другой. Искомая вероятность равна

Пример 3. Возьмем три коллектива по сто человек в каждом, один из которых состоит исключительно из блондинов, другой — из брюнетов, а третий — из шатенов. Пусть в каждом из них имеется то же самое распределение по росту, что и в рассмотренном выше примере. Перемешаем коллективы и получим новый коллектив из трехсот человек. Ясно, что при таком перемешивании распределение по росту не изменилось, причем рост индивидуума не зависит от цвета его волос. Вероятности того, что индивидуум будет брюнетом, блондином или шатеном равны между собой и равны 1/3. Вопрос: какова вероятность, что наугад выбранный человек окажется брюнетом с ростом в пределах от 175 см до 180 см?
Ответ получается на основе закона умножения вероятностей:
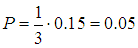
Средние величины. Понятие статистического среднего, по сути дела, ничем не отличается от привычного нам понятия среднего арифметического и является его прямым обобщением. В рассматриваемом примере у нас имеется ряд значений роста индивидуума. Под арифметическим средним мы понимаем отношение суммы всех значений некоторой величины к полному их числу, то есть сумму вида
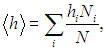
где hi — значение роста, Ni — число индивидуумов, имеющих это значение роста, N — полное число индивидуумов (измерений).
|
Статистическое среднее величины h, которое мы будем обозначать через
|
где, соответственно определению, Pi — вероятность того, что величина h имеет значение hi.
Для случая вычисления среднего роста в рассмотренном выше примере получаем

В случае непрерывно распределенных событий мы должны будем вычислить соответствующий интеграл
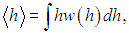
взятый в пределах всей области изменения переменной h.
В этом разделе, являющемся центральным для данной темы, устанавливается вид так называемого распределения Максвелла.
Газ, предоставленный самому себе и находящийся в постоянных внешних условиях, приходит в состояние равновесия. С макроскопической точки зрения в нем устанавливаются постоянная температура и постоянное давление. Если газ состоит из нескольких компонентов (как, например, воздух), то и состав газа в разных местах в сосуде будет одинаков. Молекулы газа даже в равновесии движутся беспорядочно, сталкиваясь между собой и со стенками сосуда, беспрерывно меняя свою скорость. Однако не все столь хаотично, как кажется на первый взгляд. Как бы ни изменялись скорости отдельных молекул, среднее значение квадрата скорости, как это следует из формулы (1.14) молекулярно-кинетической теории идеальных газов) остается постоянным и равным
|
|
|
(3.6) |
Зададим вопрос: сколько молекул (или лучше, какая доля молекул) движется с определенной скоростью (смотри ниже о том, что имеется в виду под «с определенной скоростью») в данный момент? Из предположения о хаотическом характере молекулярного движения следует, что возможно появление молекул с любыми скоростями, так что распределение молекул по скоростям надо характеризовать непрерывной функцией. Несмотря на полную хаотичность молекулярных движений, несмотря на случайный характер столкновений и вызываемых ими изменений скоростей молекул, их распределение по скоростям, как показывают теория и опыт, оказывается вполне определенным. На характер распределения по скоростям не влияют даже внешние поля при условии, что состояние системы является равновесным.
Будем считать, что возможные значения скорости заключены в интервале от 0 до бесконечности. В реальных системах скорость не может быть бесконечно большой, так как всякая система состоит из большого, но конечного числа молекул. Поэтому даже если представить себе такой практически невероятный случай, при котором все молекулы остановятся, передав всю энергию одной единственной молекуле, то и тогда энергия этой молекулы и, следовательно, ее скорость будет конечной. Мы здесь даже не говорим об ограничениях, налагаемых теорией относительности, согласно которой скорость любой молекулы не может превысить скорость света. Очень малые и очень большие по сравнению со средним значением скорости мы будем считать в принципе возможными, но, как мы убедимся, они окажутся маловероятными.
Прежде чем приступить к рассмотрению закона распределения молекул газа по скоростям, выясним сущность задачи о распределении. Определить распределение молекул по скоростям, казалось бы, означает определить число молекул, обладающих той или иной заданной скоростью. Однако в такой постановке вопрос не имеет смысла, так как число молекул, имеющих точно (математически точно!) заданную скорость, равно нулю. Действительно, число различных значений скорости бесконечно велико (непрерывное множество), число же молекул конечно. Поэтому число молекул, приходящихся на долю каждого точно заданного значения скорости, равно нулю. Вследствие этого вопрос должен быть сформулирован иначе: сколько молекул (или какая доля молекул) обладает скоростями, лежащими в некотором интервале вблизи заданной скорости?
Итак, найти распределение молекул по скоростям — это означает определить, сколько молекул или какая доля молекул из общего числа N обладают скоростями, лежащими в интервале от v до v + Dv.
Функция распределения молекул по скоростям. В дальнейшем речь, прежде всего, пойдет о распределении вероятностей для вектора скорости  , то есть о том, какова вероятность следующего события: вектор скорости
, то есть о том, какова вероятность следующего события: вектор скорости 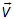 имеет проекции на оси некоторой декартовой системы координат в пространстве скоростей одновременно принадлежащие следующим интервалам
имеет проекции на оси некоторой декартовой системы координат в пространстве скоростей одновременно принадлежащие следующим интервалам
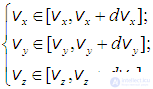
О чем можно сказать и так: конец вектора 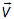 находится внутри элемента объема в пространстве скоростей
находится внутри элемента объема в пространстве скоростей
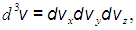
или: вектор 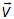 принадлежит элементу объема
принадлежит элементу объема  . При использовании в пространстве скоростей не декартовой, а, к примеру, сферической системы координат, изменится лишь набор координат и форма записи элемента объема. При использовании сферической системы координат будем иметь следующее:
. При использовании в пространстве скоростей не декартовой, а, к примеру, сферической системы координат, изменится лишь набор координат и форма записи элемента объема. При использовании сферической системы координат будем иметь следующее:
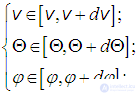
где 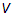 — модуль вектора скорости,
— модуль вектора скорости, 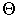 — полярный и
— полярный и 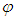 — азимутальный углы, характеризующие направление вектора
— азимутальный углы, характеризующие направление вектора 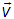 . При этом элемент объема в пространстве скоростей имеет вид
. При этом элемент объема в пространстве скоростей имеет вид
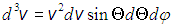 .
.
Для сокращения записи удобно также, кроме вектора 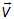 , ввести его приращение
, ввести его приращение 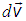 :
:
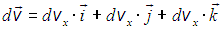 .
.
Здесь 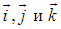 , как обычно, орты декартовых осей
, как обычно, орты декартовых осей 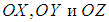 . Соответствующее выражение в сферических координатах мы не выписываем.
. Соответствующее выражение в сферических координатах мы не выписываем.
Тогда, поставленный выше вопрос можно сформулировать и так: «какова вероятность следующего события»: вектор скорости 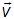 принадлежит (векторному) интервалу от
принадлежит (векторному) интервалу от 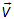 до
до 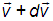
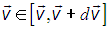 .
.
Последнее выражение можно было бы написать и сразу, однако векторы не образуют упорядоченного множества: неправомерен вопрос, какой вектор больше 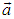 или
или 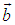 , поэтому и приведены выше разъяснения того, что имеется ввиду под принадлежностью вектора некоторому (векторному) интервалу. Векторный интервал определяет объем в соответствующем пространстве, внутри которого лежит конец вектора, а сам вектор — положение этого объема.
, поэтому и приведены выше разъяснения того, что имеется ввиду под принадлежностью вектора некоторому (векторному) интервалу. Векторный интервал определяет объем в соответствующем пространстве, внутри которого лежит конец вектора, а сам вектор — положение этого объема.
Различия в словах и обозначениях не меняют сути дела, но весьма удобны. Ничто не меняется при переходе от бесконечно малого объема 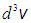 (интервала
(интервала  ) к конечному объему
) к конечному объему 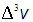 (интервалу
(интервалу 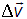 ).
).
Если DN — число молекул, имеющих при заданном состоянии системы вектор скорости в интервале от  до
до 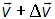 , то это число, в общем случае, вообще говоря, зависит от:
, то это число, в общем случае, вообще говоря, зависит от:
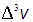 (интервала
(интервала 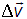 );
);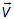 (так как при одинаковых по величине элементах объема, но при
(так как при одинаковых по величине элементах объема, но припродолжение следует...
Часть 1 3. Распределение молекул по скоростям и координатам
Часть 2 3.3. Характерные скорости молекул - 3. Распределение молекул по скоростям
Часть 3 3.4. Распределение молекул по координатам - 3. Распределение молекул по
Часть 4 - 3. Распределение молекул по скоростям и координатам
Комментарии
Оставить комментарий
Молекулярная физика и термодинамика
Термины: Молекулярная физика и термодинамика