Лекция
Это продолжение увлекательной статьи про .
...
разных его положениях в пространстве скоростей, в общем случае, число частиц будет различным).
Таким образом,

Однако, выше было заявлено и обосновано, что в состоянии термодинамического равновесия распределение молекул по направлениям движения изотропное. На «языке» функции 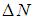 это означает, что она может зависеть только от модуля вектора скорости и не может зависеть от его направления.
это означает, что она может зависеть только от модуля вектора скорости и не может зависеть от его направления.
Следовательно, во-первых,

Во- вторых, естественно предположить, что при достаточно малых величинах объема  , число молекул в нем (число молекул с вектором скорости, принадлежащем этому объему) будет пропорционально его величине, то есть
, число молекул в нем (число молекул с вектором скорости, принадлежащем этому объему) будет пропорционально его величине, то есть

Можно показать, что при стремлении объема в пространстве скоростей  к нулю, написанное выше приближенное равенство переходит в точное. Введенная выше функция
к нулю, написанное выше приближенное равенство переходит в точное. Введенная выше функция  имеет простой смысл: это концентрация частиц в пространстве скоростей
имеет простой смысл: это концентрация частиц в пространстве скоростей
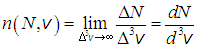
В-третьих, представляется очевидным, что чем больше частиц в системе, тем «при прочих равных» будет больше частиц и в объеме  и их концентрация
и их концентрация  . Поэтому естественно от концентрации частиц перейти к удельной величине не зависящей от полного числа частиц в системе
. Поэтому естественно от концентрации частиц перейти к удельной величине не зависящей от полного числа частиц в системе

Эта функция зависит только от скорости и дает относительное количество (долю) молекул, имеющих скорость в единичном объеме в пространстве скоростей вблизи скорости с модулем  . Эта функция
. Эта функция  называется функцией распределения молекул для вектора скорости. Если взять несколько порций одного и того же газа, находящихся в идентичных условиях (одинаковы р и Т), то распределение молекул по скоростям в них также будет идентично. Зная вид
называется функцией распределения молекул для вектора скорости. Если взять несколько порций одного и того же газа, находящихся в идентичных условиях (одинаковы р и Т), то распределение молекул по скоростям в них также будет идентично. Зная вид  , можно найти количество молекул dN из общего числа молекул N, проекции вектора скорости которых одновременно принадлежат интервалам
, можно найти количество молекул dN из общего числа молекул N, проекции вектора скорости которых одновременно принадлежат интервалам

Это число равно
 ,
,
или, при использовании сферических координат в пространстве скоростей,

Подчеркнем, что это распределение вероятностей для вектора скорости, то есть сразу для трех величин: либо для 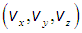 либо для
либо для 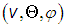 , в зависимости от используемой в пространстве скоростей системы координат. Об этом говорит сайт https://intellect.icu .
, в зависимости от используемой в пространстве скоростей системы координат. Об этом говорит сайт https://intellect.icu .
Концентрация частиц в пространстве скоростей должна подчиняться условию, имеющему простой физический смысл: число молекул со всевозможными векторами скорости, которым соответствуют все возможные объемы  , на которые можно разбить все пространство скоростей, должно быть равно полному числу частиц в системе. При переходе к пределу, то есть от
, на которые можно разбить все пространство скоростей, должно быть равно полному числу частиц в системе. При переходе к пределу, то есть от 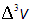 к
к  , суммирование превращается в интегрирование по всему пространству скоростей и мы имеем:
, суммирование превращается в интегрирование по всему пространству скоростей и мы имеем:
|
|
|
(3.10) |
откуда следует условие нормировки функции распределения
 .
.
Вычисление, написанного выше, нормировочного интеграла разумеется возможно при использовании любой системы координат в пространстве скоростей. Например, в декартовой системе
 .
.
Однако, «грех» не воспользоваться фактом изотропности распределения молекул по направлениям движения, отражением которого является зависимость функции распределения  только от модуля вектора скорости. В сферических координатах нормировочный интеграл имеет существенно проще, так как два из трех интегрирований можно провести в общем виде:
только от модуля вектора скорости. В сферических координатах нормировочный интеграл имеет существенно проще, так как два из трех интегрирований можно провести в общем виде:
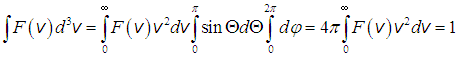
Функция распределения для газов была найдена теоретически Максвеллом (1859) и носит его имя. Далее мы установим ее вид.
Распределение Максвелла. Поскольку все направления движения молекул в пространстве равноправны, распределение скоростей должно быть изотропным и функция распределения n(v) не может зависеть от направления скорости. Это означает, что n(v) не может быть произвольной функцией от компонент скорости vх, vy, vz, а должна зависеть лишь от абсолютной величины скорости

В зависимости от выбранной системы координат вероятность  имеет различный вид.
имеет различный вид.
В декартовой системе
|
|
|
(3.11) |
В цилиндрической системе
|
|
|
(3.12) |
В сферической системе
|
|
|
(3.13) |
Далее предлагается простой, хотя и не вполне строгий вывод вида функции распределения. Рассмотрим процесс столкновения двух частиц, движущихся со скоростями v1 и v2. Пусть в результате соударения скорости молекул изменяются и превращаются в vi и v4. Число таких столкновений в единицу времени в единице объема газа должно быть пропорционально числу молекул со скоростями вблизи v1 и v2, то есть произведению n(v1)·n(v2). Рассмотрим далее процесс соударения, являющийся обратным данному. При этом скорости молекул изменяются от значений v3 и v4 до значений v1 и v2. Число таких соударений в единицу времени в объеме пропорционально количеству молекул со скоростями вблизи v3 и v4, то есть n(v3)·n(v4).
В силу предположения о молекулярном хаосе и предположения о том, что число молекул с данными значениями скорости не изменяется процессами молекулярных столкновений в газе, находящемся в стационарном состоянии, можно считать, что число молекул, у которых скорости изменяются от значений v1 и v2 до значений v3 и v4, равно числу молекул, у которых скорости изменяются от v3 и v4 до v1 и v2. Отсюда следует, что
|
|
|
(3.14) |
Равенство (3.14) выражает баланс частиц, получающих и теряющих соответствующую скорость, причем в процессе таких упругих соударений энергия молекул сохраняется (m0 — масса молекулы):
|
|
|
(3.15) |
Равенства (3.10), (3.14) и (3.15) представляют совокупности условий, которым должна удовлетворять искомая функция распределения.
Используя (3.15), выразим v4 через v1, v2, v3:
|
|
|
(3.16) |
Функциональные уравнения (3.14) и (3.16) легко превратить в простое дифференциальное уравнение. Взяв логарифм от (3.14), имеем
|
|
|
(3.17) |
Продифференцируем (3.17) по аргументу v1:
|
|
|
(3.18) |
Аналогично
|
|
|
(3.19) |
Учитывая выражение (3.16), находим
|
|
|
(3.20) |
Подставляя (3.20) в правые части соотношений (3.18) и (3.19), приходим к равенству
|
|
|
(3.21) |
При этом мы должны помнить, что это равенство справедливо при совершенно произвольных значениях v1, v2, которые являются независимыми переменными. Это значит, что равенство (3.21) должно иметь место при совершенно произвольных значениях скоростей, поэтому оно может быть выполнено только тогда, когда правая и левая части (3.21) равны некоторой постоянной (которую мы обозначим через ( –α)):
|
|
|
(3.22) |
где переменная v может принимать значения v1, v2 или любое иное. Разделяя переменные, записываем (3.22) в виде
|
|
|
(3.23) |
Интегрируя (3.23), находим
|
|
|
(3.24) |
где А — постоянная интегрирования. Из физических соображений очевидно, что

Большие скорости молекул маловероятны. Поэтому коэффициент α > 0. Постоянная А определяется из условия нормировки (3.10):
|
|
|
(3.25) |
Далее будет показано, что параметр α должен быть связан с абсолютной температурой T соотношением
|
|
|
(3.26) |
С учетом (3.26) из (3.24) получим
|
|
|
(3.27) |
Формула (3.27) и представляет собой искомое распределение молекул по скоростям.
Учитывая, что n(v) зависит только от модуля скорости, а их направления равновероятны, можно ввести функцию распределения f(v) молекул по абсолютной величине скорости. Для этого надо проинтегрировать выражение (3.13) по углам, что дает
|
|
|
(3.28) |
Отсюда и из (3.27) следует выражение для функции распределения Максвелла для модуля вектора скорости f(v):
|
|
|
(3.29) |
Величина f(v)dv есть вероятность найти частицу с модулем скорости, лежащим в интервале от v до v + dv. Условие нормировки распределения f(v) принимает теперь вид
|
|
|
В этом разделе приводятся некоторые следствия, вытекающие из формул (3.29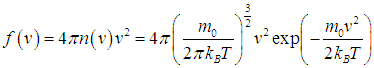 ) и (3.30
) и (3.30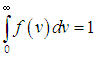 ). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах Т1 = 300 К и Т2 = 1 300 К.
). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах Т1 = 300 К и Т2 = 1 300 К.
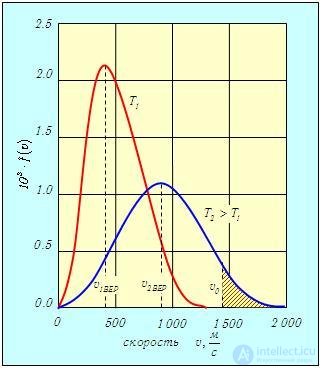
Рис. 3.3. Распределение молекул кислорода по скоростям при разных температурах T1 = 300 К и T2 = 1 300 К
Наиболее вероятная скорость. При бесконечно малых и неограниченно больших значениях скоростей функция распределения стремится к нулю

то есть такие предельные значения скоростей маловероятны в системе. Следовательно, при каком-то значении скорости функция f(v) достигает своего максимума.
|
Наиболее вероятная скорость vВЕР — это скорость, отвечающая максимальному значению функции распределения. |
Ее можно найти, решая уравнение

откуда следует, что
|
|
|
(3.31) |
Иными словами, наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул. В этой точке f(v) принимает максимальное значение:
|
|
|
(3.32) |
Соотношения (3.31), (3.32) могут быть полезны для анализа изменения функции распределения при изменении температуры газа или при изменении рода газа, то есть массы молекул. Отметим, что как следует из (3.26) – (3.29), распределение Максвелла зависит не отдельно от массы молекул и отдельно от температуры газа, а от их отношения  . Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для молекулярного водорода
. Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для молекулярного водорода 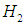
 при температуре
при температуре 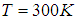 и для гелия
и для гелия 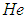
 при температуре
при температуре  .
.
С ростом температуры наиболее вероятная скорость vВЕР (3.31) увеличивается, то есть максимум функции f(v) сдвигается вправо (см. рис. 3.3), Т2 > Т1. При этом f(vВЕР) уменьшается, то есть кривая становится более пологой. Так же деформируется кривая, если температура постоянна, но масса молекул уменьшается. Напомним, что при любых деформациях функции распределения f(v) площадь под кривыми постоянна и равна единице в соответствии с формулой (3.30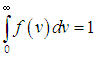 ).
).
Относительное количество молекул, скорость которых превышает некоторое значение v0, определяется выражением
|
|
|
(3.33) |
На графике (см. рис. 3.3) этому интегралу соответствует лежащая справа от v0 часть площади (отмечена штриховкой), ограниченная кривой f(v) и осью скоростей. Как видно из рис. 3.3, относительное количество молекул, имеющих скорости, превышающие v0, растет с повышением температуры.
В заключение этого раздела заметим, что во всех формулах для функции распределения и характерных скоростей входит отношение массы молекулы к постоянной Больцмана

Умножая числитель и знаменатель на число Авогадро NA и учитывая, что

— молярная масса газа, a

— универсальная газовая постоянная, мы всюду можем использовать это отношение в наиболее удобной для конкретной задачи форме

Распределение молекул по величинам безразмерной скорости. Если при графическом изображении функции распределения Максвелла (3.29) по оси абсцисс откладывать скорости молекул v, то форма кривой и положение максимума будут зависеть от массы молекул и от температуры газа. Но если по горизонтальной оси откладывать отношение скорости к наиболее вероятной скорости, то есть безразмерную скорость
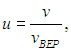
то для всех температур и любых масс молекул (любых газов) получится одна и та же кривая (рис. 3.4).

Рис. 3.4. Распределение Максвелла по величинам безразмерной скорости
Сделав замену переменной
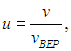
в (3.29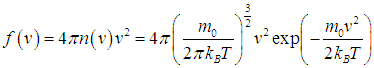 ) и учитывая, что
) и учитывая, что

получим распределение Максвелла в форме
|
|
|
(3.34) |
Эта формула и соответствующий ей график (см. рис. 3.4) удобны для решения многих задач.
Пример. Найдем, какая часть общего числа молекул кислорода имеет при температуре 27 °С скорости, отличающиеся от наиболее вероятной не более, чем на 1 %; а также скорости в интервале 562–572 м/с.
Произведем необходимые вычисления. Чтобы ответить на первый вопрос задачи, учтем, что u = 1 при v = vВЕР. Величина интервала du = 0,02. Следовательно,

Вычислим наиболее вероятную скорость:

Найдем отношение v = 562 м/с к vВЕР = 395 м/с

Определим по кривой (см. рис. 3.4) значение функции f(u) при u = 1,42. Получаем f(u) = 0,62. Ширина интервала Dv = 10 м/с (Du = 10/395 = 0,0253). Следовательно, доля молекул в этом интервале

Интересно отметить, что молекула кислорода проходит за секунду путь, равный в среднем 0,4 км. Но не нужно забывать о соударениях молекул. Из-за них молекула по прямой движется очень недолго, и ее путь представляет собой ломаную линию. Поэтому молекула, двигаясь с огромной скоростью по отдельным звеньям ломаной траектории, передвигается от слоя к слою газа со сравнительно небольшой скоростью.
Средняя арифметическая скорость. Знание функции распределения молекул по скоростям f(v) дает возможность найти среднее значение скорости, а также любой величины, являющейся функцией скорости, например квадрата скорости v2 или кинетической энергии молекулы mv2/2.
|
Средняя арифметическая скорость |
Разобьем интервал всех возможных значений скорости от 0 до бесконечности на малые интервалы Dvi. Каждому интервалу соответствует количество молекул
|
|
|
(3.35) |
Так как интервалы Dvi, малы, то можно приближенно считать скорости молекул данного интервала одинаковыми и равными vi. Сумма значений скоростей молекул интервала
|
|
|
(3.36) |
Сумма значений скоростей всех молекул
|
|
|
(3.37) |
Разделив эту сумму на число молекул, получим выражение для средней арифметической скорости
|
|
|
(3.38) |
Переходя от суммы к интегралу, получаем
|
|
|
(3.39) |
Вычисляя интеграл, получаем среднюю арифметическую скорость молекул
|
|
|
(3.40) |
Среднеквадратичная скорость. Чтобы найти среднее значение произвольной функции L(v) скорости, нужно эту функцию умножить на функцию распределения и проинтегрировать по всем возможным значениям
продолжение следует...
Часть 1 3. Распределение молекул по скоростям и координатам
Часть 2 3.3. Характерные скорости молекул - 3. Распределение молекул по скоростям
Часть 3 3.4. Распределение молекул по координатам - 3. Распределение молекул по
Часть 4 - 3. Распределение молекул по скоростям и координатам
Комментарии
Оставить комментарий
Молекулярная физика и термодинамика
Термины: Молекулярная физика и термодинамика