4. Явления переноса законы и теория

Привет, Вы узнаете о том , что такое явления переноса, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое явления переноса, броуновское движение , настоятельно рекомендую прочитать все из категории Молекулярная физика и термодинамика.

В предыдущих главах мы имели дело с равновесными системами. В результате движения молекул, перераспределения энергии между ними в различных частях системы устанавливаются равновесные температура, концентрация частиц. Например, в отсутствии внешних полей концентрация частиц будет одинаковой во всех частях системы, находящейся в равновесии. Во внешнем гравитационном поле концентрация частиц меняется в зависимости от высоты, но имеет строго определенное значение и одинакова в горизонтальном направлении.

В реальных системах, однако, возникают ситуации, когда система не находится в состоянии равновесия. Между частями системы может возникнуть перепад (градиент, если говорить на научном языке) температур, концентрации частиц, плотности, импульса. Тогда в системе возникнут потоки соответствующей характеристики в направлении, обратном ее градиенту, так что система будет приближаться к состоянию термодинамического равновесия. Такого рода процессы относятся к явлениям переноса; они ответственны, как мы увидим в этой главе, за теплопроводность тел, вязкость жидкости, диффузию частиц (рис. 4.1). Здесь мы по-прежнему пользуемся молекулярно-кинетическим подходом. Наша цель - понять, каким образом блуждающие молекулы переносят те или иные физические характеристики в другие части системы.

Рис.4.1. Модель диффузии частиц через отверстие

4.1. Столкновения молекул

Говоря об идеальном газе, мы исходили из того, что молекулы не взаимодействуют между собой. На самом деле предполагалось, конечно, отсутствие потенциальной энергии взаимодействия между ними. Упругие столкновения между молекулами и молекул со стенками обязательно должны происходить хотя бы потому, что иначе будет отсутствовать механизм, с помощью которого устанавливается равное распределение энергии по степеням свободы, иначе нельзя будет говорить о температуре системы, давлении в ней и т. п. Столкновения молекул происходят случайно. Они приводят к изменению направления и величины скорости частиц, но не меняют распределения молекул по скоростям и координатам в равновесных системах.

Возникает вопрос: а всегда ли молекулы будут сталкиваться друг с другом? Ведь молекулы очень малы, а расстояния между ними в идеальном газе на порядок больше их линейных размеров. Быть может, для сосудов малых размеров они летят без соударений от стенки к стенке? Подсчитаем, сколько раз в единицу времени одна молекула может столкнуться с другими и какое расстояние она пролетает в среднем между столкновениями.

Прежде чем перейти к вычислениям, примем простейшую модель для молекул. Будем представлять их в виде упругих шариков. При столкновении молекул с эффективными диаметрами d₁ и d₂ их центры сближаются на расстояние (d₁ + d₂)/2 (рис. 4.2).

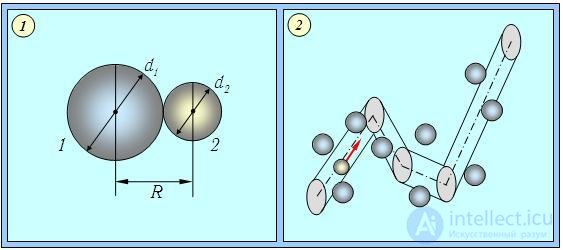
Рис. 4.2. Столкновение двух молекул (1) и траектория движения выделенной молекулы газа (2): направление ее движения меняется, когда какая-то из молекул среды попадает в радиус взаимодействия R = (d_t + d₂)/2

Если представить себе, что молекула 1 налетает на молекулу 2, то столкновение произойдет; если первая молекула попадет в сферу радиусом

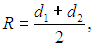
описанную вокруг второй молекулы. Площадь сечения этой сферы

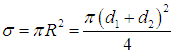
Величина R называется эффективным радиусом взаимодействия молекул 1 и 2, а — эффективным сечением взаимодействия этих молекул. При столкновении одинаковых молекул d₁ = d₂ = d, R = d и

За время между двумя последовательными столкновениями молекула пролетает некоторый путь l. Разумеется, для каждой отдельной молекулы дело чистой случайности, сколь далеко ей удастся продвинуться без столкновений. Но усредняя путь l по всем молекулам системы, получим физическую величину

называемую средней длиной свободного пробега молекул. Статистический смысл этой величины таков: отношение малого отрезка длиной dx к дает вероятность столкновения

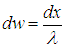
на пути dx. Пусть Р(х) — вероятность пролететь без столкновений расстояние х. Тогда

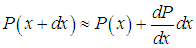
— вероятность, пролететь без столкновений расстояние х + dx. Последнее событие складывается из двух независимых событий:

частица пролетела без столкновений расстояние х (вероятность чего равна Р(х));

частица также без столкновений преодолела еще и маленький отрезок пути dx (вероятность чего равна 1 – dx/). По теореме об умножении вероятностей имеем тогда

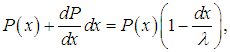
откуда следует уравнение для вероятности Р(х)

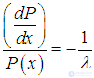
Поскольку вероятность преодолеть нулевое расстояние без столкновений равна единице, имеем дополнительно начальное условие Р(0) = 1. Интегрируя дифференциальное уравнение, находим окончательно

Как видно, чем больше путь х, тем меньше вероятность преодолеть его без столкновений.

Убедимся теперь, что — действительно средняя длина свободного пробега. Вычислим, с какой вероятностью молекула будет иметь длину свободного пробега l. Это значит, что частица пролетела без столкновений расстояние х = l (вероятность чего есть Р(l)) и столкнулась с другой частицей непосредственно за этим — на малом отрезке длиной dl (вероятность чего можно найти как dl/). Вероятность dw такого события по теореме умножения вероятностей равна

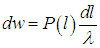
Находим тогда среднюю длину свободного пробега

He следует думать, конечно, что вероятность преодолеть расстояние l без столкновений равна нулю: часть молекул может пролететь очень большие расстояния, но лишь крайне небольшая их часть. При х = , как следует из (4.1), вероятность пролета без столкновений равна

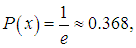
то есть 63,2 % частиц испытают столкновения на этом пути. При длине пути х = 2 получаем

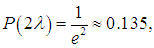
то есть столкновения суждены уже 86,5 % частиц, при х = 3 в столкновениях участвует уже 95 % частиц, поскольку

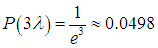
Чтобы определить среднее число столкновений n одной молекулы с другими в единицу времени, сделаем следующие допущения:

• все молекулы одинаковы, то есть мы не рассматриваем смеси газов;
• все молекулы, за исключением той, за которой мы наблюдаем, неподвижны (в дальнейшем мы покажем, как избавиться от этого заведомо неверного предположения);
• при столкновениях скорость v_ОT молекулы не меняется (это предположение, в сущности, того же уровня, что и предыдущее: при упругом столкновении с препятствием, которое остается неподвижным, модуль скорости действительно не меняется (смысл подстрочного индекса «от» станет ясным в дальнейшем)).

Путь нашей молекулы диаметром d остается прямолинейным до тех пор, пока ей не встретится неподвижная молекула, чей центр окажется от линии движения на расстоянии, меньшем R = d. После этого молекула сменит направление движения и будет двигаться прямолинейно до нового соударения. За интервал времени ∆t молекула пройдет ломаный путь v_OT ∆t и столкнется со всеми молекулами, попавшими в ломаный цилиндр радиусом d и площадью основания = pd ² (см. рис. 4.1). Объем этого цилиндра равен pd ² v_OT ∆t. Если n-концентрация молекул в системе (их число в единице объема), то легко найти количество неподвижных молекул в цилиндре, то есть число столкновений DN:

Отсюда следует частота столкновений (то есть число столкновений в единицу времени)

Избавимся теперь от последствий нашего предположения о неподвижности молекул. Пусть мы следим за молекулой 1, которая движется со скоростью v₁, и она сталкивается с молекулой 2, имеющей скорость v₂. В системе отсчета, связанной со второй молекулой, она неподвижна, зато первая молекула имеет скорость

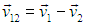
Ясно теперь, что именно среднее значение относительной скорости молекул играет роль скорости v_ОТ, использованной нами при выводе соотношения (4.3) для частоты столкновений. Имеем тогда

где 𝜃₁₂ — угол между направлениями движения молекул. Из-за хаотичности движения этот угол равновероятно принимает любые значения, так что среднее значение его косинуса равно нулю. А усреднение квадратов скоростей приводит к появлению среднеквадратичной скорости молекул

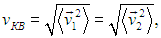
знакомой нам по предыдущей главе. Получаем в итоге, что

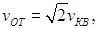
и формула (4.3) записывается в окончательном виде

Заметим, что, перейдя от скорости молекулы к ее среднеквадратичной скорости, мы на самом деле избавились и от третьего допущения, поскольку v_KB постоянна при заданной температуре.

Зная частоту столкновений, можно найти среднюю длину свободного пробега. Действительно, среднее время между двумя последовательными соударениями = 1/n, и за это время частица в среднем проходит путь = vKBt. Таким образом, средняя длина свободного пробега молекулы газа равна

Поскольку при постоянной температуре концентрация частиц пропорциональна давлению, то с ростом давления длина свободного пробега уменьшается. Это и понятно, так как уменьшается среднее расстояние между частицами. На самом деле молекула не является твердым шариком. Поэтому ее эффективный диаметр d-величина не совсем постоянная: он уменьшается при увеличении температуры, хотя и незначительно. Поэтому средняя длина свободного пробега слегка растет с повышением температуры.

Следует отметить, что среднее расстояние между частицами далеко не совпадает со средней длиной свободного пробега. Ранее мы оценили эффективный диаметр молекулы водяного пара d = 3·10^{–10 м} и среднее расстояние между молекулами при нормальных условиях L = 3·10^–9 м. Отсюда находим концентрацию молекул

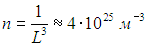
Подставляя найденное n в выражение для длины свободного пробега, находим

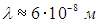
Мы видим, что длина свободного пробега в 200 раз больше диаметра молекулы и в 20 раз больше среднего расстояния между молекулами. Для полноты картины оценим также частоту столкновений. Кинетическая энергия поступательного движения молекулы

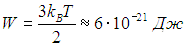
Зная массу молекулы воды

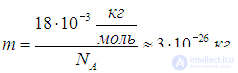
получаем оценку среднеквадратичной скорости

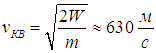
Наконец, определяем

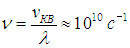
Иначе говоря, молекула испытывает 10 млрд соударений в секунду! Линейный размер сосуда, содержащего один литр газа, равен l = 10 см = 0,1 м. При скорости 630 м/с молекула могла бы пролететь путь от стенки до стенки за время

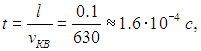
но за это время она испытает

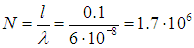
столкновений с другими молекулами.

У нас осталось без обсуждения первое допущение об одинаковости всех молекул. Оно было нужно не по принципиальным соображениям, а для упрощения вывода и окончательных выражений. Если это не так, если мы рассматриваем смесь газов, то компоненты имеют разные концентрации частиц, различные среднеквадратичные скорости, а их молекулы — разные массы. Как следствие, изменится формула для средней длины свободного пробега, причем результаты будут отличаться для молекул различных сортов.

Пример. Найдем, как изменится формула (4.6) для средней длины свободного пробега молекул, если они представляют собой плоские диски, двигающиеся в материале тонкой пленки, будучи не в состоянии из нее вылететь?

Как и прежде, для столкновения молекул диаметрами d₁ и d₂ они должны сблизиться на расстояние

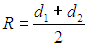
Поэтому при движении молекулы по плоскости пленки она заденет все другие молекулы, которые попадут в ломаный прямоугольник (в отличие от цилиндра в трехмерном случае) шириной 2R и длиной v_OT ∆t. Площадь этого прямоугольника

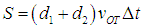
При поверхностной концентрации n молекул (в этом случае n — их число на единицу площади) произойдет ∆N = Sn столкновений. Отсюда для частоты столкновений находим

где мы учли, что, как и прежде, относительная скорость

Отсюда длина свободного пробега для движущихся в плоскости плоских молекул получается равной

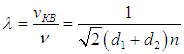
При одинаковых молекулах (d₁ = d₂ = d)

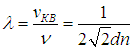
Свидание в лесу, ежик в тумане и атомная бомба. Идея длины свободного пробега может быть использована для оценки видимости в лесу, в тумане или даже для грубой оценки критической массы урана в атомной бомбе.

Представьте себе, что у вас назначено свидание в лесу. С какого максимального расстояния R вы заметите своего партнера (а партнер — вас)? Положим, вы включаете фонарик, чтобы подать ему/ей сигнал. Если не учитывать рассеяние света, то все деревья отбрасывают тени, линейный размер которых можно считать примерно равным диаметру d деревьев. На рис. 4.3 ваше место нахождения отмечено красным кружком, вокруг проведена окружность радиусом R, деревья показаны зелеными кружками, а их тени на окружности отмечены оранжевыми дугами.

Рис. 4.3. Оценка максимального расстояния R видимости в лесу

Определим, какую часть окружности покрывают тени. Пусть n плотность посадки деревьев (их число на единицу площади). Если l — среднее расстояние между деревьями, то

Внутрь окружности попадает pR²n деревьев. Полная длина тени на окружности равна поэтому pR²nd. Мы видим, что полная длина тени растет как квадрат радиуса и при каком-то значении R превысит длину окружности 2pR. Но если вся окружность покрыта тенями, то свет дальше не пройдет. Это значение R и будет максимальным расстоянием видимости в лесу. Теперь понятно, что оно определяется из равенства

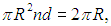
то есть мы получили оценку

Для численного примера можно взять значения, исходя из своего жизненного опыта. Скажем, свидание назначено среди березок со средним диаметром ствола d = 0,25 м и средним расстоянием между деревьями l = 10 м. Тогда находим R = 800 м.

Установим теперь связь полученного результата с формулой для средней длины свободного пробега. У нас одна молекула (световой луч) не имеет размера (d₁ = 0), размер прочих молекул равен среднему диаметру ствола (d₂ = d) и, наконец, молекулы (стволы) — покоятся, то есть надо отбросить множитель 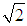. Получаем в результате — применительно к нашей задаче — выражение

Таким образом, найденный нами радиус видимости

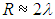
Вероятность свету преодолеть это расстояние без «столкновений» с деревьями равна

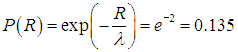
Иными словами, с вероятностью 86.5 % свет будет задержан деревьями.

Свидание в лесу происходило на плоскости. Сейчас мы вернемся в объемный мир. Тот же рисунок изображает теперь сферу радиусом R и препятствия в виде шариков диаметром d. Например, мы хотим оценить видимость для ежика, заблудившегося в тумане, и роль деревьев теперь исполняют водяные капли. Если концентрация капель равна п (их число в единице объема), то внутри сферы находится

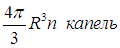
Их тени на сфере представляют собой окружности площадью pd²/4. При максимальном расстоянии видимости тени покрывают всю сферу:

Отсюда находим расстояние видимости в тумане

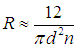
Снова сравним этот результат с формулой (4.6) для длины свободного пробега молекулы в газовой среде, где надо отбросить фактор и взять

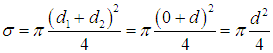
Получаем

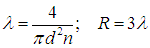
Вероятность преодолеть путь R = 3l без столкновений равна

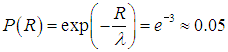
Стало быть, с вероятностью 95 % столкновение на этом пути произойдет.

Получим численную оценку. Наши рассуждения годятся, если размер капель заметно (скажем, на один-два порядка) превышает длину световой волны. Так как видимый диапазон имеет длины волн 0,40–0,76 мкм, то для диаметра капель примем оценку d = 10^–4 м. Для концентрации капель возьмем значение n = 3·10⁷ м^–3 (о происхождении этого числа см. чуть ниже). Тогда видимость в тумане будет

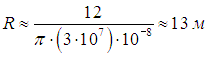
Концентрацию капель мы оценили следующим образом. Давление насыщенного водяного пара при, скажем, 20 °С (Т = 293 К) равно р_Н = 2,3·10³ Па. Применяя уравнение Клапейрона — Менделеева, находим плотность водяного пара при 100 % влажности:

При резком понижении температуры весь пар конденсируется в капли указанного размера — образуется густой туман. Масса одной капли равна

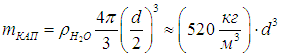
Количество образовавшихся капель в объеме V находим как отношение массы пара m к массе капли m_КАП. Об этом говорит сайт https://intellect.icu . Тогда концентрация капель определится из соотношения

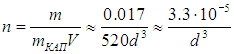
При d = 10^–4 м получаем использованное выше значение n = 3·10^–7 м^–3.

Зависимость расстояния видимости в тумане от размера капель дается, таким образом, соотношением

При предельно малых капельках с диаметром порядка десяти длин световой волны d = 10^–5 м видимость сокращается до одного метра. Что называется, «не видно дальше своего носа». При еще меньших размерах капель наша модель становится неверной, так как свет уже нельзя рассматривать просто как совокупность частиц с ничтожно малым размером. Начинают играть роль эффекты дифракции, и выражение для эффективного сечения взаимодействия света с каплями уже не будет определяться чисто геометрическим сечением капель.

Решенная задача имеет также отношение к вопросу о критической массе урана-235, применяемого для изготовления атомных бомб. Вместо света в этой задаче мы имеем нейтроны, а вместо капель — ядра ²³⁵U. При столкновении с ядрами нейтроны расщепляют их на осколки, и при этом вылетает еще 3–4 нейтрона. При критическом радиусе R_крит количество нейтронов не будет уменьшаться и возникнет самоподдерживающаяся цепная реакция — произойдет атомный взрыв. За основу определения критического радиуса можно взять радиус видимости

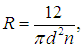
уменьшенный в kраз (k = 3,5 — коэффициент размножения нейтронов). Поскольку

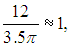
получаем

Радиус ядра

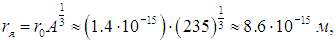
где r₀ = 1,4·10^-15 м — радиус ядра с массовым числом А = 1, то есть протона (нейтрона). Поэтому эффективный диаметр взаимодействия равен

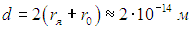
В справочнике (например, Российском энциклопедическом словаре) находим плотность урана r_U = 19·10³ кг/м³. Массу ядра урана-235 определяем по массе протона

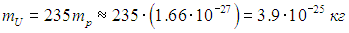
Отсюда находим концентрацию ядер

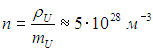
Теперь мы можем оценить критический радиус R_крит

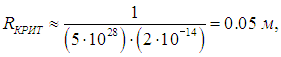
критический объем V_крит

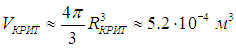
и критическую массу М_крит

Отметим, что никаких секретов производства ядерного оружия мы не выдаем: слишком грубы эти оценки. Единственная наша цель — продемонстрировать еще раз единство законов физики, действующих в самых разнообразных системах.

4.2. Законы процессов переноса

Если газ выведен из состояния равновесия, то в нем возникают процессы, стремящиеся вернуть систему в равновесное состояние. Например, разные части системы имеют разные температуры или концентрации частиц. Соответственно, температуры или концентрации стремятся выровняться (за счет теплового движения молекул), что сопровождается передачей (переносом) тех или иных физических величин от одной части системы к другой. Такие процессы называются явлениями переноса. Эти явления имеют много общего и классифицируются по тому признаку, какая именно физическая характеристика «переносится» из одной части системы в другую.

Диффузия. Пусть в системе имеются молекулы, концентрация которых n(z) зависит от координаты z. Мысленно поместим в точке с координатой z квадратик площадью S, ортогональный оси z. В системе происходит процесс выравнивания концентрации n частиц, сопровождающийся их переносом в направлении убывания n. Эксперимент показал, что через площадь S за единицу времени проходит количество частиц

где D определяется свойствами системы и называется коэффициентом диффузии. Величина Ф (поток частиц — число частиц в единицу времени) имеет размерность

размерность концентрации частиц

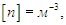
и поэтому размерность коэффициента диффузии

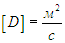
Отрицательный знак в законе диффузии как раз и означает, что поток частиц направлен от больших значений концентрации к меньшим, то есть в направлении, противоположном производной dn/dz. Действительно, пусть n(z) — убывающая функция, то есть концентрация частиц падает с ростом z. Тогда производная dn/dz (градиент концентрации) отрицательна, а поток Ф получается положительным, то есть направлен в сторону увеличения z.

Если обе части уравнения (4.7) умножить на массу m₀ диффундирующих молекул, то для потока массы М = m₀Ф получим аналогичное уравнение

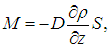
где r = т₀n — масса диффундирующего вещества в единице объема, то есть его плотность. Связь (4.7) потока частиц с градиентом dn/dz концентрации называется первым законом Фика.

Первый закон Фика ничего не говорит о величине коэффициента диффузии, который должен в каждом конкретном случае определяться экспериментально. Поэтому этот закон носит эмпирический характер. Он применим не только для газов, но и для твердых и жидких тел. Следует отметить также, что перенос вещества в газах и жидкостях может осуществляться и механическим путем за счет конвекционных потоков (скажем, за счет ветра в атмосфере или течения в океане). Важно не путать диффузию, которая происходит из-за молекулярного движения, с конвекцией, возникающей вследствие воздействия внешних сил.

Заметим, что если система является смесью, то первый закон Фика записывается точно в такой же форме для каждого из компонентов смеси в отдельности, но коэффициенты диффузии, вообще говоря, различаются. Это значит, что в смеси, скажем, двух газов может случиться так, что концентрация частиц одного из компонентов уже выровнялась, а второго — еще нет.

Второй закон Фика позволяет найти зависимость концентрации диффундирующих частиц от времени. Для его вывода рассмотрим два параллельных друг другу одинаковых квадратика, расположенных в близких точках с координатами z и z + dz. Для определенности будем считать, что n(z) — убывающая функция (рис. 4.4).

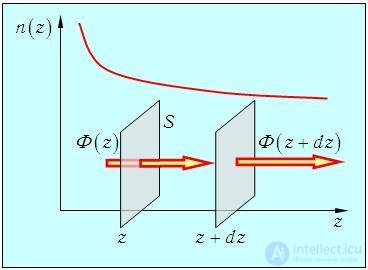
Рис. 4.4. Иллюстрация явления диффузии (к выводу второго закона Фика)

Тогда через левую площадку за время dt входит Ф(z)dt частиц, а через правую выходит Ф(z + dz)dt частиц.

Увеличение числа частиц dN в пространстве между площадками за время dt равно разности числа входящих и выходящих частиц:

Разделив dN на объем Sdz зазора между квадратиками, получаем изменение концентрации частиц за время dt

Используя первый закон Фика, находим отсюда (здесь мы уже переходим к частным производным)

Обычно коэффициент диффузии не зависит от координат, и мы получаем уравнение, выражающее второй закон Фика:

Если ввести плотность потока частиц j = Ф/S (число частиц, пересекающих единичную площадь в единицу времени), то уравнение (4.8) можно записать в иной форме:

Это уравнение — один из примеров уравнения непрерывности, встречающегося во многих областях физики и выражающего в данном случае закон сохранения числа частиц. Его смысл: скорость изменения числа частиц в объеме равна разности потоков входящих и выходящих частиц (при условии, что внутри объема не происходит рождения или исчезновения частиц).

Вязкость. Рассмотрим следующий мысленный опыт. Пусть на поверхности жидкости плавает пластина, которую медленно тянут направо с силой F_T (рис. 4.3).

Рис. 4.5. Сила внутреннего трения F, действующая на пластину, движущуюся со скоростью u₀, по поверхности жидкости

Опыт показывает, что при установившемся движении пластина перемещается с постоянной скоростью u₀. Пусть расстояние до неподвижного дна равно d, а площадь пластины равна S. Что мы можем сказать о течении жидкости?

Ясно, что кроме силы F_T на пластину должно действовать что-то еще: иначе она двигалась бы равноускоренно. Это «что-то еще» может действовать только со стороны жидкости. Другими словами, на пластину со стороны жидкости действует сила F, подобная силе трения. Она направлена влево и по величине равна действующей силе F_T. Каково происхождение этой силы? Прилегающий к пластине слой жидкости «прилипает» к ней и движется с той же скоростью u₀. Аналогично слой жидкости, прилегающий ко дну, имеет нулевую скорость. Следовательно, в системе устанавливается некоторое распределение скоростей u(z), где z — расстояние от дна. В конечном итоге неподвижное дно через жидкость действует на пластину, порождая силу внутреннего трения, уже знакомую нам из механики жидкостей и газов.

Видео 4.2. Сила внутреннего трения в газе: опыт с дисками.

В соответствии со сказанным, заведомо должны выполняться граничные условия u(0) = 0, u(d) = u₀. Сила внутреннего трения возникает как раз вследствие этого распределения скоростей: вышележащий слой «трется» о нижележащий и тормозится им (соответственно, более быстрый слой стремится ускорить более медленный).

Опыт показывает, что сила внутреннего трения F связана со скоростью u₀ соотношением (см. рис. 4.3)

Коэффициент h, имеющий размерность

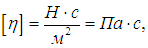
называется коэффициентом динамической вязкости (внутреннего трения).

Чтобы найти распределение скоростей в этой системе, представим себе наблюдателя, находящегося на расстоянии z от дна и движущегося вместе с жидкостью со скоростью u(z). С точки зрения этого наблюдателя, его слой покоится, а пластина движется со скоростью u₀ – u(z). Зависимость той же силы F от скорости должна теперь описываться аналогичной формулой с заменой

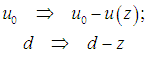
В результате получаем

Приравнивая выражения (4.11) и (4.12), находим скорость слоя как функцию расстояния от дна

Мы получили линейный закон распределения скоростей (рис. 4.6), удовлетворяющий нашим граничным условиям u(0) = 0, u(d) = u₀.

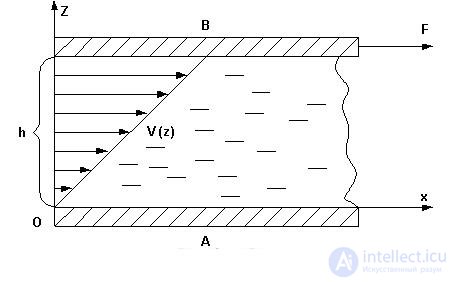
Рис. 4.6 Линейное распределение скоростей в жидкости

Такое распределение скоростей связано с простотой рассмотренной системы. В других случаях течение имеет более сложный характер, но и тогда мы можем воспользоваться найденной закономерностью. Действительно, рассмотрим жидкость, в которой существует градиент скоростей по координате z. Относительная скорость слоев с координатами z и z + dz равна

Поскольку мы рассматриваем сколь угодно малые расстояния dz, то для малых площадей S течение можно считать плоским и описываемым прежними формулами. Тогда сила внутреннего трения между соседними слоями будет определяться уравнением (4.11), где вместо отношения u₀/d стоит градиент скорости относительного движения слоев du/dz:

Такой закон действительно соответствует опытам по определению силы внутреннего трения между слоями жидкости или газа при ламинарном течении и был установлен Ньютоном.

Теплопроводность. Предположим теперь, что есть два источника тепла различной температуры Т₁ и Т₂. Представим их себе как широкие пластины, расположенные перпендикулярно оси z в точках с координатами z = 0 и z = d. Газ, заполняющий зазор между пластинами, передает тепловую энергию от горячего тела к более холодному. При этом в газе устанавливается некоторое распределение температур T(z), удовлетворяющее граничным условиям Т(0) = T₁ и T(d) = Т₂ (рис. 4.).

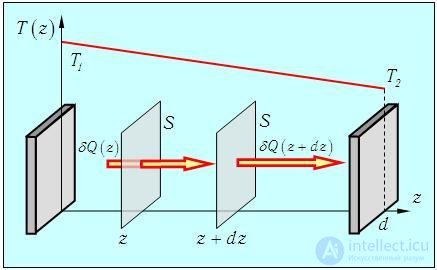
Рис. 4.7. Распределение температуры между двумя источниками

Поместим между источниками квадратик площадью S, параллельный пластинам. Опыт показывает, что за время dt через площадь S протекает количество теплоты dQ, причем

Постоянная k называется коэффициентом теплопроводности и имеет размерность

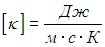
Соотношение (4.15) называется законом Фурье.

Отрицательный знак (как и в первом законе Фика) указывает, что поток тепла направлен в сторону понижения температуры, то есть против градиента температуры dT/dz. При этих условиях в равновесном состоянии в газе установится линейный закон изменения температуры. Действительно, через квадратик единичной площади, расположенный в точке z, в единицу времени втекает количество теплоты

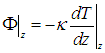
Через такой же квадратик в точке z + dz в единицу времени вытекает теплота

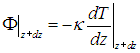
Если температура между квадратиками не меняется (установилось равновесие), то эти потоки теплоты равны между собой, то есть

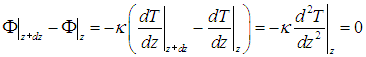
Из равенства нулю второй производной следует, что функция линейна:

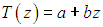
Из граничных условий в концевых точках находим константы интегрирования:

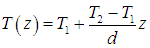
В сущности, мы получили аналог закона распределения скоростей при рассмотрении вязкости жидкости: достаточно заменить

Это следствие стационарности, то есть того факта, что мы рассматривали установившееся течение или распределение температур. То же следует из второго закона Фика: для стационарной системы: производная по времени в левой части уравнения (4.9) равна нулю, откуда следует равенство нулю второй производной концентрации частиц по координате z, что эквивалентно линейности функции n(z).

Пример. Определим, какое количество тепловой энергии уносится в единицу времени через окно площадью S = 2 м² с расстоянием между стеклами d = 5 см, если в комнате поддерживается температура t₁ = 20 °С, а на улице стоит мороз:
t₂ = –20 °С.

Сразу заметим, что поскольку величина градуса по шкалам Цельсия и Кельвина одинакова, то разность температур

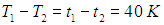
Коэффициент теплопроводности воздуха k = 0,025 Дж/(м·с·К). Для стекла этот коэффициент в 20 раз больше, так что его наличие можно не учитывать. К тому же толщина стекла много меньше промежутка между стеклами. Поэтому от мороза нас оберегает именно воздушная прослойка между стеклами. В соответствии со сказанным, в этом промежутке устанавливается линейное распределение температуры, так что производная dT/dz постоянна и равна

Поток тепловой энергии равен тогда

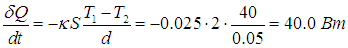
Расход тепловой энергии через одно окно за месяц

Решая эту задачу, мы неявно сделали сильное предположение, что температура внутреннего стекла совпадает с температурой в комнате, а наружного — с температурой окружающего воздуха. Из практики каждый знает, что это не так: на самом деле наружная поверхность стекла несколько теплее, а внутренняя - немного холоднее. В действительности градиент температур в промежутке между рамами может быть раза в два меньше, что соответственно уменьшает поток тепловой энергии наружу. Однако точное решение задачи выходит за рамки данного курса.

Нетрудно заметить то общее, что есть у всех обсуждавшихся явлений. Во все уравнения переноса входит градиент некоторой величины — концентрации частиц, скорости течения, температуры. Во всех случаях при условии стационарности устанавливается линейное распределение этой величины. Все это потому, что явления переноса имеют общее происхождение — молекулярное движение.

4.3. Кинетическая теория переноса

Изложенные выше законы, описывающие явления переноса — первый закон Фика и аналогичные законы для внутреннего трения и теплопроводности, — были установлены экспериментально. В этом разделе мы покажем, что они следуют из молекулярно-кинетической теории. Основу всех явлений переноса составляет хаотическое движение молекул. При переходе в другие части системы молекулы переносят туда информацию о тех условиях, в которых они пребывали прежде. Перенос массы (или сам переход частиц) характерен для явления диффузии. Перенос энергии от одних слоев газа к другим составляет сущность процесса теплопроводности. И, как мы увидим, перенос импульса лежит в основе явления внутреннего (молекулярного) трения газа или жидкости.

Диффузия. Проведем сначала анализ процесса диффузии (точнее, самодиффузии, то есть диффузии каким-то образом выделенных молекул в среде, состоящей из таких же частиц). В этом случае средние скорости частиц среды и диффундирующих частиц одинаковы, а длина свободного пробега дается уже знакомым выражением

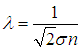
Выделим мысленно в среде какую-то площадку S и направим ось z ортогонально к ней. Две другие оси х и у параллельны площадке. Хаотичность движения молекул смоделируем следующим образом. Будем считать, что ровно 1/3 молекул движется вдоль оси х, 1/3 — вдоль оси у и 1/3 — вдоль оси z. Из молекул, летящих параллельно z, ровно половина (1/6 часть полного числа молекул) движется в положительном направлении, и столько же - в отрицательном. Подсчитаем количество молекул, пересекающих площадь S в единицу времени (рис. 4.8).

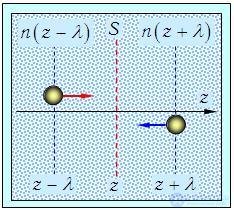
Рис. 4.8. Встречные потоки частиц через площадку S из областей с различной концентрацией частиц (к выводу первого закона Фика)

Ясно, что молекулы, летящие вдоль осей х и у, площадку не пересекут. За время dt молекулы преодолевают расстояние dt. Потому на площадку попадет только 1/6 часть молекул из объема dtS справа и 1/6 часть молекул из того же объема слева. Но концентрации частиц слева и справа различны (n зависит от z).

Внимательный читатель может спросить: ведь мы фиксируем бесконечно малый промежуток времени dt, следовательно, и рассматриваемые объемы — диски бесконечно малой толщины dt. Поэтому, казалось бы, и концентрации частиц слева и справа должны совпадать. Вопрос правилен, но дело в том, что последний раз перед попаданием на площадку S молекулы сталкивались с другими молекулами на расстоянии длины свободного пробега l от площадки. Поэтому к выделенной нами площади они подходят с теми концентрациями частиц n(z – l) и n(z + l), которые сложились в точках с координатами z – l и z + l соответственно (z — координата площадки). Слева на площадку попадет число частиц dN₁, a справа — dN₂, причем эти числа будут различаться:

(4.16)

Поскольку l мало, можем разложить концентрации частиц в ряд, удерживая только два первых члена:

(4.17)

Полное число частиц dN, пересекающих площадку в положительном направлении оси z, равно разности чисел частиц, пересекающих площадку слева и справа. Находим тогда

(4.18)

Выражение для потока частиц

(4.19)

по структуре в точности совпадает с первым законом Фика (4.7). Стало быть, мы не только вывели этот закон, но и определили коэффициент диффузии:

(4.20)

Учитывая, что

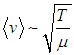
и что

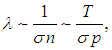
(4.21)

Такая зависимость коэффициента диффузии в газах от температуры и давления подтверждается экспериментом.

Вязкость. Рассмотрим теперь механизм возникновения вязкости газа. Ось z теперь будем представлять расположенной вертикально в соответствии с рис. 4.9.

Рис. 4.9. Встречные потоки частиц через площадку S из областей с различной скоростью упорядоченного движения частиц (к выводу закона вязкости)

Предположим теперь, что концентрация частиц одинакова во всех частях системы, так что числа частиц

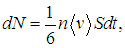
приходящих снизу и сверху, равны. Однако молекулы приходят из слоев, имеющих разные скорости упорядоченного (не молекулярного!) движения u(z). Когда более медленная молекула из нижнего слоя попадает в верхний, она притормаживает его упорядоченное движение, а сама ускоряется. Наоборот, молекулы из верхнего слоя ускоряют нижний и тормозятся им. Таким образом, этот процесс способствует выравниванию скоростей в системе, а именно в этом и заключается явление внутреннего трения (вязкости).

Мы предполагаем, что скорость упорядоченного движения много меньше средней скорости теплового движения молекул (составляющей сотни метров в секунду). Тогда среднюю скорость теплового движения можно по-прежнему считать постоянной. Для импульсов упорядоченного движения, переносимого через площадь S снизу и сверху, имеем

(4.22)

Отсюда для полного импульса, переносимого в положительном направлении оси z, получаем

(4.23)

В этой формуле мы использовали плотность газа

Переносимый импульс параллелен скорости u, а его направление зависит от знака производной. При распределении скоростей, показанном на рис. 4.3, скорость растет с ростом z, так что производная

Знак минус в уравнении (4.23) означает, что импульс, поступающий снизу от более медленных слоев, меньше импульса, поступающего сверху, от более быстрых слоев. Поэтому импульс слоя с координатой z в данном случае стремится возрасти на величину –dp. Производная

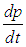
дает силу, действующую на слой жидкости площадью S и имеющий координату z

(4.24)

Мы вывели закон (4.14) и получили выражение для коэффициента динамической вязкости

(4.25)

Теперь нетрудно установить зависимость коэффициента динамической вязкости от температуры и рода газа:

(4.26)

Обратите внимание, что коэффициент динамической вязкости не зависит в конечном итоге от плотности, то есть от давления. Это происходит потому, что с ростом давления увеличивается плотность газа, но и пропорционально растет концентрация частиц, то есть уменьшается длина свободного пробега. Эти два фактора компенсируют друг друга.

Теплопроводность. Проанализируем теперь явление теплопроводности. Предположим, что концентрация частиц в системе всюду одинакова, так что слева и справа площадку пересекает одинаковое число частиц, как и при рассмотрении диффузии:

(4.27)

так что полный поток частиц через площадку S (рис. 4.10, сравни с рис. 4.8) равен нулю.

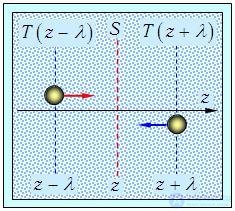
Рис. 4.10. Встречные потоки частиц через площадку S из областей с различной температурой газа (к выводу закона теплопроводности)

Однако молекулы приносят с собой те средние энергии w, которыми они обладали в слоях с координатами z – l и z + l. Эти энергии пропорциональны температуре:

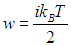
Умножая среднюю энергию на число частиц, пересекающих площадку, получаем для переносимого ими количества энергии слева и справа

(4.28)

Для тепла, переносимого в положительном направлении оси z, отсюда получаем выражение

(4.29)

Мы вывели закон (4.15) и нашли коэффициент теплопроводности

(4.30)

Видео 4.3. Теплопроводность газов. Бутан – воздух при одинаковых и разных давлениях.

Напомним, что i — эффективное число определяющее среднюю энергию молекулы. Поскольку

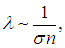
то коэффициент теплопроводности не зависит от концентрации молекул или плотности газа. Зависимость его от температуры Т и рода газа такова:

(4.31)

Видео 4.4. Теплопроводность газов. Неон – воздух при одинаковом давлении.

Видео 4.5. Теплопроводность газов. Воздух – воздух при разном давлении.

Введем удельную теплоемкость газа при постоянном объеме

и учтем далее, что масса молекулы равна

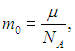
откуда следует связь концентрации частиц с плотностью газа

Тогда получим для коэффициента теплопроводности несколько иное выражение:

(4.32)

Из проведенного анализа следуют формулы связи между соответствующими коэффициентами переноса (см. соотношения (4.20), (4.25) и (4.32)):

(4.33)

Приведем численные оценки, использовав полученные ранее результаты для водяного пара, характерные при нормальных условиях для всех газов: плотность

Тогда находим коэффициенты диффузии

теплопроводности (i = 6 для водяного пара)

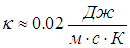
и динамической вязкости

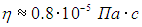
Сравним полученные оценки с опытными данными для воздуха:

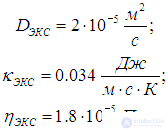
Мы видим, что не ошиблись, по крайней мере, в порядках величин, хотя наши оценки коэффициентов и не совсем точны.

4.4. броуновское движение

Задача о блуждающем матросе. Решим сначала классическую задачу о пьяном матросе. Матрос выходит из кабачка и собирается направиться домой. Он движется с постоянной скоростью v но в состоянии поддерживать выбранное направление движения лишь на пути l, то есть в течение времени

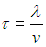
После этого его разворачивает, он теряет ориентировку и движется в каком-то другом направлении. Выбор направления каждый раз происходит случайным образом, так что любые направления равновероятны. Спрашивается, на каком среднем расстоянии R_KB от кабачка будет находиться матрос в момент времени t (предполагается, что 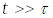). Слово «среднее» здесь означает следующее. Предположим, что такое происходит каждый день, и каждый раз мы измеряем удаление матроса от кабачка. Среднее квадратичное полученных значений при большом числе испытаний (скажем, за год) и дает нам искомую величину R_KB.

Рис. 4.11. Модель броуновского движения

Видео 4.6. Физическая модель броуновского движения.

Итак, возьмем кабачок за начало отсчета координат и будем характеризовать положение матроса в момент времени радиус-вектором R. Путь матроса состоит из ломаных линий, число которых k = t/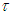. Пусть i — номер линии (i = 1, 2, ..., k). Перемещение матроса по линии с номером i задаем вектором r_i, так что для всех значений i имеем (рис. 4.12)

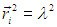
Рис. 4.12. Траектория блуждающего матроса

Тогда радиус-вектор R представляется в виде суммы векторов r_i

Возведем в квадрат обе части равенства (4.34):

Здесь 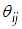— угол между векторами r_i и r_j. Усредним теперь обе части равенства (4.35) по всем случаям похода матроса в кабачок. Средние значения всех косинусов равны нулю в силу равновероятности выбора матросом следующего направления движения после прямого отрезка. Получаем тогда

Отсюда следует искомое среднеквадратичное расстояние

Заметим, что это расстояние зависит от квадратного корня из времени в отличие от случая прямолинейного и равномерного движения. Это существенно меняет характер движения. Приведем численный пример. Пусть матрос движется медленно, со скоростью v = 0,9 км/ч = 0,25 м/с. За время t = 3 ч = 10 800 с при прямолинейном движении он удалился бы на расстояние 0,9·3 = 2,7 км. Предположим, что по прямой он в состоянии двигаться только 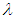= 10 м. Тогда среднее его удаление от кабачка за то же время составит

Броуновское движение и диффузия. Оставив нашего матроса петлять в окрестностях кабачка, мы вправе задать вопрос: а какое он имеет отношение к молекулярно-кинетической теории? Оказывается, самое прямое. Пусть в воде плавает пылинка, за которой мы наблюдаем в микроскоп. Пылинка подвергается ударам со стороны молекул среды, случайным образом меняя свое направление движения и скорость.

Случайность траектории пылинки здесь связана с тем, что:

• с разных сторон ее может ударить различное число молекул
• молекулы, ударяющие с одной стороны, могут в этот момент иметь большие скорости, нежели молекулы, ударяющие с другой.

Поэтому пылинка движется по ломаной траектории. Это явление называется броуновским движением. С повышением температуры интенсивность броуновского движения растет. При увеличении размеров пылинки случайности ее столкновения с молекулами сглаживаются, и броуновское движение становится ненаблюдаемым. Броуновское движение является самым непосредственным доказательством хаотического характера движения молекул. Наш блуждающий матрос — имитация броуновского движения. На этой простой задаче мы продемонстрировали характерную особенность — зависимость среднеквадратичного смещения пылинки от корня из времени движения. Произведение 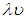в уравнении (4.43) имеет ту же размерность и ту же структуру, что и коэффициент диффузии. Поэтому для броуновского движения также следует ожидать зависимости среднеквадратичного смещения вида

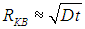
Броуновское движение тесно связано с диффузией. Обратимся ко второму закону Фика (4.9). Это уравнение первого порядка по времени, и оно позволяет найти функцию n(z, t) если задана начальная концентрация числа частиц n(z, 0). Мы не будем решать эту задачу точно. Отметим только, что с течением времени начальное распределение «расплывается» в пространстве и при этом изменяет свою форму. Но есть один вид распределения — гауссово, или нормальное распределение, — форма которого со временем остается неизменной (оно лишь «расплывается»). Мы займемся только этим, самым простым, случаем, позволяющим тем не менее получить все характерные особенности процесса. Для вычислений нам понадобятся два стандартных интеграла:

Пусть распределение концентрации частиц в начальный момент времени t = 0 имеет вид

Вид этой функции представлен на рис. 4.13

Рис. 4.13. Расплывание гауссова распределения концентрации частиц с течением времени: три кривые соответствуют трем различным значениям времени, измеренного в единицах t = l²(0)/(2D); по оси абсцисс отложены «безразмерные» расстояния, измеренные в единицах полуширины l(0) начального распределения; по оси ординат показано отношение концентрации частиц n(z, t) к ее максимальному значению n(0, 0) в начальный момент времени t = 0; горизонтальные отрезки показывают среднеквадратичную ширину 2l(t)/l(0) каждого из распределений

Видео 4.7. «Генерация» распределения Гаусса с помощью зерен пшена.

Здесь N — полное число частиц, распределенных по оси z с концентрацией n(z, 0):

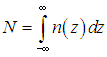
Величина l(0) характеризует ширину распределения. Действительно, выражение

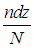
дает относительное число частиц на интервале (z, z + dz), то есть вероятность частице оказаться на этом отрезке. Поэтому среднее значение квадрата координаты равно

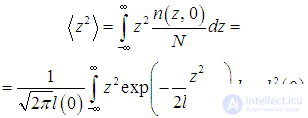
Если определить ширину распределения как расстояние между точками

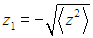
и

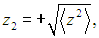
то

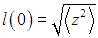
есть среднеквадратичная полуширина распределения в начальный момент времени t = 0.

Как уже было сказано, гауссово распределение — единственное, не меняющее своей формы при расплывании. Это значит, что в произвольный момент времени t распределение будет иметь вид

Соответственно, для произвольного момента времени

где пока неизвестная функция l(t) есть меняющаяся полуширина распределения.

Наша задача упростилась: вместо решения дифференциального уравнения в частных производных (4.9), нам достаточно теперь подставить туда (1), убедиться, что оно действительно является решением, и найти зависимость полуширины распределения от времени, то есть определить функцию l(t).

Продифференцируем (1) по координате z:

Продифференцируем (1) по z еще раз, принимая во внимание результат первого дифференцирования:

Теперь продифференцируем (1) по времени:

Подставляя выражения (2) и (3) в уравнение (4.9) второго закона Фика, убеждаемся, что n(z, t) в форме (4.46) действительно является его решением, если полуширина распределения l(t) удовлетворяет уравнению

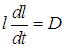
Это уравнение легко интегрируется:

или

откуда находим зависимость полуширины распределения от времени:

Если в начальный момент времени t = 0 все молекулы были сосредоточены в одном месте (l(0) = 0), то

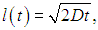
что на новом уровне воспроизводит результат, угаданный нами при анализе блужданий матроса. Увеличение полуширины распределения дает смещение броуновской частицы. Выражение для среднеквадратичного смещения броуновской частицы

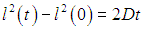
— это классический результат Эйнштейна — Смолуховского, построивших теорию броуновского движения.

Пример. В аудиторию входит студентка. Оценим время, через которое запах ее духов достигнет экзаменатора, сидящего за столом.

Коэффициент диффузии молекул в газах мы оценили как

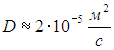
Расстояние l(t) до экзаменатора примем равным 4 м, а ширина начального распределения примерно равна диаметру головы студентки l(0) = 0.2 м. Поскольку l(t) >> l(0), можно воспользоваться уравнением (4.52), откуда находим

Ответ явно несуразен и противоречит всему мировому опыту приема экзаменов. Из этого примера ясно, что распространение запахов по комнате происходит не вследствие диффузии, а из-за более быстрых процессов. Оказывается, наш нос способен реагировать на считанное число молекул, поэтому для ощущения запаха достаточно, чтобы носа экзаменатора достигли лишь несколько штук самых быстрых молекул с «хвоста» распределения Максвелла. Плюс, конечно, конвекция: открываемая студенткой дверь создает поток воздуха, который переносит молекулы духов достаточно быстро.

Численные оценки для броуновского движения. Если диффузионные процессы столь медленны, то как удалось наблюдать броуновское движение? Для ответа на этот вопрос мы оценим сейчас коэффициент диффузии пылинки в жидкости. Мы уже знаем, что квадрат среднеквадратичного смещения частицы вдоль какой-то оси линейно зависит от времени:

Этот закон можно использовать для определения коэффициента диффузии броуновских частиц. Рассмотрим теперь уравнение движения частицы вдоль выбранной оси z:

Здесь F_z — случайная сила, действующая на частицы со стороны молекул, а второй член в правой части — сила сопротивления движению частицы вследствие вязкости жидкости по закону Стокса (предполагается, что броуновские частицы являются шариками радиусом r). Поскольку нас интересует зависимость от времени квадрата координаты z, мы умножим уравнение (2) на z и используем соотношения

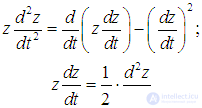
Усредняя получившееся уравнение, приходим к выражению

Здесь учтено, что z> = 0 из-за случайности сил, воздействующих на пылинку со стороны молекул. В силу (1)

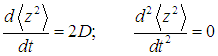
Подставляя эти значения в (3) и учитывая, что

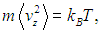
находим искомое выражение для коэффициента диффузии броуновских частиц

Выполним теперь численные оценки. Радиус броуновских частиц (пылинок) r = 0,5·10^–6 м. Принимая h = 10^–3 Па·с (вода) и Т = 300 К, получаем из (4)

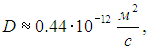
что гораздо меньше коэффициента диффузии молекул духов студентки из рассмотренного выше примера. Тем не менее, броуновское движение наблюдаемо. Скажем, за 30 с среднеквадратичное смещение частицы составит

что в пять раз превышает диаметр пылинки. Поэтому такие смещения можно наблюдать в микроскоп. Пример демонстрирует известную научную истину: сами по себе величины не могут априори считаться малыми или большими, все познается в сравнении.

Исследование, описанное в статье про явления переноса, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое явления переноса, броуновское движение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Молекулярная физика и термодинамика