Лекция
Привет, Вы узнаете о том , что такое сфера, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое сфера , настоятельно рекомендую прочитать все из категории Стереометрия.
Расстояние от точки сферы до ее центра называется радиусом сферы. Сфера радиуса 1 называется единичной сферой.
Сфера так же имеет объем и площадь поверхности.
Пожалуй, кроме определения, разница заключается в том, что в задачах никогда не находят объем сферы. Как правило, ищут объем шара. Это не значит, что у сферы нет объема. Это трехмерная фигура, поэтому объем у нее есть.
Еще одно отличие, которое можно считать более или менее значимым: секущая плоскость сферы: окружность, которая не имеет внутреннего пространства, но имеет длину. Секущая плоскость шара: круг, который имеет площадь и не имеет длины окружности.
Шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова « сфайра» - мяч. При этом слово « шар» образовалось от перехода согласных сф в ш. В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом. В древности сфера была в большом почете. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. Сфера всегда широко применялось в различных областях науки и техники.
Сфера является поверхностью вращения, образованной при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учетом непостоянства значения размеров дуг составляет 41252,96 кв. градусов.

 Сфера — поверхность шара
Сфера — поверхность шара
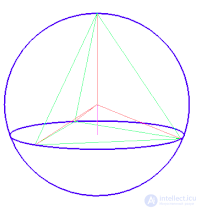
Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара. Сфера имеет наименьшую площадь из всех поверхностей, ограничивающих данный объем, также из всех поверхностей с данной площадью сфера ограничивает наибольший объем. Поэтому тела сферической формы встречаются в природе, например, маленькие капли воды при свободном падении приобретают сферическую форму именно из-за минимизации площади поверхности силой поверхностного натяжения.
Объем цилиндра, объем вписанного в него шара, касающегося обоих его оснований, и объем конуса, с вершиной в центре одного основания цилиндра и с основанием, совпадающим с другим основанием цилиндра, находятся в соотношении 3 : 2 : 1 .
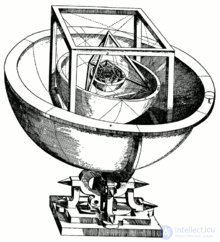
«Кубок Кеплера»: модель Солнечной системы из пяти правильных многогранников и их вписанных и описанных сфер.
Совершенство сферической формы издавна привлекало внимание мыслителей и ученых, которые с помощью сфер пытались объяснить гармонию окружающего мира. Древнегреческий ученый Пифагор вместе с шарообразной Землей в центре Вселенной ввел окружающую Землю удаленную хрустальную сферу, к которой прикреплены звезды, и семь более близких вращающихся хрустальных сфер, к которым прикреплены Солнце, Луна и пять известных к тому времени планет (исключая Землю). Эта модель впоследствии усложнялась: Евдокс Книдский рассматривал уже 27 подобных сфер, а Аристотель — 55 хрустальных сфер . Представления о вращающихся небесных сферах господствовали по крайней мере до средних веков и даже вошли в гелиоцентрическую систему мира Николая Коперника, который назвал свой основной труд «О вращении небесных сфер» (лат. De revolutionibus orbium coelestium).
Небесные сферы со времен Древней Греции были частью более общей концепции гармонии сфер о музыкально-астрономическом устройстве мира, куда также входило понятие «музыка сфер». Эта концепция также существовала как минимум до средневековья. У одного из известнейших астрономов, Иоганна Кеплера, сфера занимала центральное место во всей его системе религиозно-мистических представлений, он писал: «Образ триединого бога есть сферическая поверхность, а именно: бог-отец в центре, бог-сын — на поверхности и святой дух — в симметричном отношении между центром и описанной вокруг него сферической поверхностью» . Одно из первых значительных сочинений Кеплера, «Тайна мироздания» (лат. Mysterium Cosmographicum), было посвящено параметрам небесных сфер, Кеплер считал, что он открыл замечательную связь между правильными многогранниками, которых только пять, и небесными сферами шести известных к тому времени планет (включая Землю), являвшимися, по Кеплеру, описанными и вписанными сферами этих многогранников. Представления о гармонии сфер сыграли большую роль при открытии Кеплером третьего закона движений небесных тел (во всяком случае, могут рассматриваться как стимул к поиску астрономических соотношений) . Однако у Кеплера небесные сферы являлись уже чисто математическими объектами, а не физически существующими телами. К тому времени Тихо Браге показал, что движение комет, в частности, Большой кометы 1577 года, несовместимо с существованием твердых небесных сфер . Как удобная математическая модель, осталась одна небесная сфера, с помощью которой астрономы по сей день представляют видимые положения звезд и планет.
Уравнение сферы в прямоугольной системе координат:
где — координаты центра сферы,
— ее радиус.
Параметрическое уравнение сферы с центром в точке :
где и
Гауссова кривизна сферы постоянна и равна 1/R².
Через четыре точки пространства может проходить единственная сфера с центром
где:
Радиус данной сферы:
Площадь поверхности сферы
Объем шара, ограниченного сферой
Площадь сегмента сферы высоты
.
Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Об этом говорит сайт https://intellect.icu . Большие окружности являются геодезическими линиями на сфере; любые две из них пересекаются в двух точках. Иными словами, большие круги сферы являются аналогами прямых на плоскости, расстояние между точками на сфере — длина дуги проходящего через них большого круга. Углу же между прямыми на плоскости соответствует двугранный угол между плоскостями больших кругов. Многие теоремы геометрии на плоскости справедливы и в сферической геометрии, существуют аналоги теоремы синусов, теоремы косинусов для сферических треугольников. В то же время, существует немало отличий, например, в сферическом треугольнике сумма углов всегда больше 180 градусов, к трем признакам равенства треугольников добавляется их равенство по трем углам, у сферического треугольника может быть два и даже три прямых угла — например, у сферического треугольника, образованного экватором и меридианами 0° и 90°.
Если даны сферические координаты двух точек, то расстояние между ними можно найти так:
Однако, если угол задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:
В этом случае и
называются широтами, а
и
долготами.
В общем случае уравнение (n−1)-мерной сферы (в n-мерном евклидовом пространстве) имеет вид:
где — центр сферы, а
— радиус.
Пересечением двух n-мерных сфер является (n−1)-мерная сфера, лежащая на радикальной гиперплоскости этих сфер.
В n-мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1 сфер.
n-мерная инверсия переводит (n−1)-мерную сферу в (n−1)-мерную сферу или гиперплоскость.
С трехмерной сферой связана одна из задач тысячелетия — гипотеза Пуанкаре, в которой утверждается, что всякое односвязное компактное трехмерное многообразие без края гомеоморфно такой сфере. Эта гипотеза была доказана Г. Я. Перельманом в начале 2000-х годов на основе результатов Ричарда Гамильтона.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
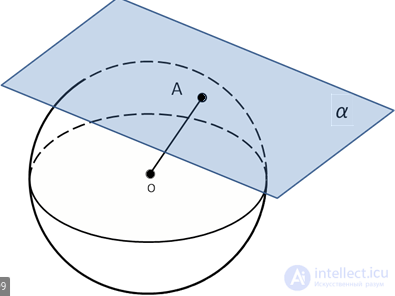
Сфера и плоскость могут:
1) пересекаться по окружности. Случай, когда расстояние от центра сферы до плоскости меньше радиуса сферы.
Тогда сечение сферы плоскостью есть окружность;
2) не пересекаться. Случай, когда расстояние от центра сферы до плоскости больше радиуса сферы.
Тогда сфера и плоскость не имеют общих точек.
3) и иметь только одну общую точку. Случай, когда расстояние от центра сферы до плоскости равно радиусу сферы.
Давайте более подробно остановимся на последнем случае, когда сфера и плоскость имеют только одну общую точку.
Определение:
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Исследование, описанное в статье про сфера, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое сфера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия