Векторы в пространстве и действия над ними

Привет, сегодня поговорим про векторы в пространстве, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое векторы в пространстве, векторы в пространстве и действия над ними , настоятельно рекомендую прочитать все из категории Стереометрия.

Вектором в пространстве называется направленный отрезок.
Координатами вектора с началом в точке A1(x1; y1; z1) и концом в точке A2(x2; y2; z2) называются числа x2-x1, y2-y1, z2-z1. Вектор обозначается в пространстве так:

векторы в пространстве и действия над ними

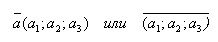
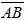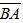Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом или . Вектор называется противоположным вектору 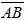и может быть обозначен .

Сформулируем ряд базовых определений.

Длиной или модулем вектора 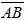называется длина отрезка и обозначается 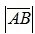. Вектор нулевой длины (его суть - точка) называется нулевым 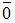и направления не имеет. Вектор 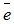единичной длины, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора .

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, записывают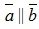. Коллинеарные векторы могут иметь совпадающие или противоположные направления. Нулевой вектор считают коллинеарным любому вектору.

Векторы называются равными , если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

Рассмотрим в пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и обозначим их через 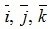соответственно. Выберем произвольный вектор пространства и совместим его начало с началом координат. Спроектируем вектор на координатные оси и обозначим проекции через ax, ay, az соответственно. Тогда нетрудно показать, что

. (2.25)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора . Таким образом, координаты вектора являются его проекциями на оси координат. Векторное равенство (2.25) часто записывают в виде

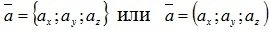. Мы будем использовать обозначение вектора в фигурных скобках, чтобы визуально легче различать координаты вектора и координаты точки. С использованием формулы длины отрезка, известной из школьной геометрии, можно найти выражение для вычисления модуля вектора :

, (2.26)

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: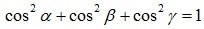Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

.

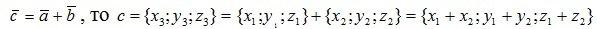Данная формула имеет место для произвольного конечного числа слагаемых.

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

2. Вычитание двух векторов производится покоординатно, аналогично сложению, то есть если , то

.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

Важным следствием вычитания векторов является тот факт, что если известны координаты начала и конца вектора, то для вычисления координат вектора необходимо из координат его конца вычесть координаты его начала. Действительно, любой вектор пространства 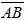может быть представлен в виде разности двух векторов, исходящих из начала координат: . Координаты векторов и совпадают с координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу вычитания векторов следует произвести вычитание координат точки А из координат точки В.

3. Умножение вектора на число λ покоординатно:.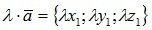

При λ>0 – вектор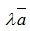 сонаправлен ; λ<0 – вектор 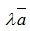противоположно направлен ; |λ|>1 – длина вектора увеличивается в λ раз; |λ|<1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A’ и B’.

Проекцией 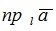вектора на ось l называется длина вектора , взятая со знаком «+», если вектор и ось l сонаправлены, и со знаком «–», если и l противоположно направлены.

Если в качестве оси l взять некоторый другой вектор 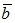, то получим проекцию вектора на вектор .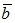

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и 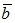называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

. Об этом говорит сайт https://intellect.icu . (2.27)

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 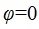, поэтому его косинус (в 2.27) равен 1.

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Теорема 2.3. Скалярное произведение двух векторов , заданных своими координатами, равно сумме произведений их одноименных координат, то есть

(2.28)

С помощью скалярного произведения векторов можно вычислить угол между ними. Если заданы два ненулевых вектора своими координатами , то косинус угла φ между ними:

(2.29)

Отсюда следует условие перпендикулярности ненулевых векторов и :

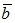(2.30)

Нахождение проекции вектора на направление, заданное вектором 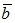, может осуществляться по формуле

(2.31)

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Предположим, что под действием постоянной силы материальная точка перемещается прямолинейно из положения А в положение B. Вектор силы образует угол φ с вектором перемещения (рис. 2.14). Физика утверждает, что работа силы при перемещении равна .

Следовательно, работа постоянной силы при прямолинейном перемещении точки ее приложения равна скалярному произведению вектора силы на вектор перемещения.

Пример 2.9. С помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

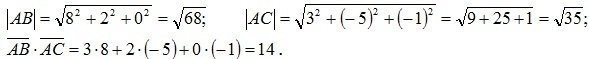
Отсюда согласно формуле (2.29) получим косинус искомого угла

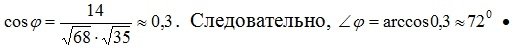
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Таблица 2.2

Решение. Введем в рассмотрение два вектора: вектор затрат ресурсов на тонну продукции 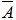и вектор цены единицы соответствующего ресурса .

Тогда . Общая цена ресурсов 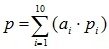, что представляет собой скалярное произведение векторов 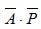. Вычислим его по формуле (2.28) согласно теореме 2.3:

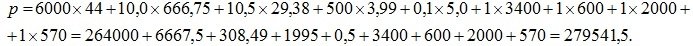
Таким образом, общая цена затрат на производство одной тонны творога составляет 279 541,5 рублей

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Пример 2.11. Вычислить работу, произведенную силой , если точка ее приложения перемещается прямолинейно из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила ?

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

. По формуле (2.28) (единиц работы).

Угол φ между и находим по формуле (2.29), то есть

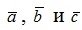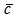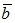6. Три некомпланарных вектора , взятые в указанном порядке, образуют правую тройку, если при наблюдении из конца третьего вектора кратчайший поворот от первого вектора ко второму вектору совершается против часовой стрелки, и левую, если по часовой стрелке.

Векторным произведением вектора на вектор 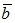называется вектор 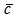, удовлетворяющий следующим условиям:

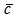– перпендикулярен векторам и ;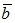

– имеет длину, равную , где φ – угол, образованный векторами и ;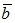

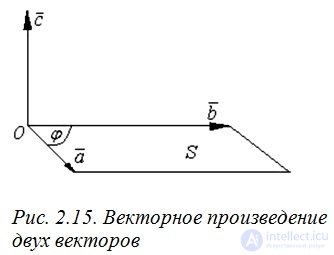
– векторы 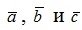образуют правую тройку (рис. 2.15).

Теорема 2.4. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения

Теорема 2.5. Векторное произведение векторов , заданных своими координатами, равно определителю третьего порядка вида

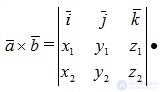(2.32)

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны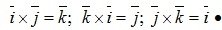

Следствие 3. Векторный квадрат любого вектора равен нулю

Геометрическая интерпретация векторного произведения состоит в том, что длина результирующего вектора численно равна площади S параллелограмма, построенного на векторах–сомножителях как на сторонах, приведенных к одному началу. Действительно, согласно определению, модуль векторного произведения векторов равен . С другой стороны, площадь параллелограмма, построенного на векторах и 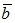, также равна . Следовательно,

. (2.33)

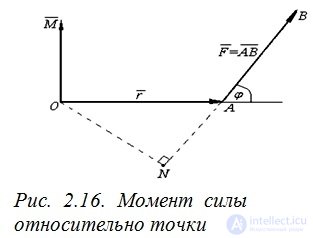
Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

Пусть в точке A приложена сила и пусть O – некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом силы относительно точки O называется вектор , который проходит через точку O и удовлетворяет следующим условиям:

- перпендикулярен плоскости, проходящей через точки O, A, B;

- его модуль численно равен произведению силы на плечо .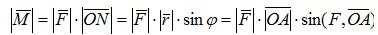

- образует правую тройку с векторами и .

Следовательно, момент силы относительно точки O представляет собой векторное произведение

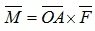. (2.34)

Линейная скорость точки М твердого тела, вращающегося с угловой скоростью вокруг неподвижной оси, определяется формулой Эйлера , O – некоторая неподвижная

точка оси (рис. 2.17).

Пример 2.12. С помощью векторного произведения найти площадь треугольника ABC, построенного на векторах 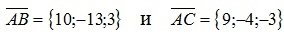, приведенных к одному началу.

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

. Согласно формуле (2.33) модуль векторного произведения двух неколлинеарных векторов численно равен площади параллелограмма, построенного на данных векторах как на сторонах, приведенных к общему началу, то есть . Тогда площадь треугольника 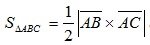. Следовательно, искомая площадь равна (единиц площади)

7. Рассмотрим произведение трех векторов 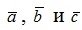, составленное следующим образом: 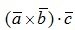. Здесь первые два вектора перемножаются векторно, а результирующий вектор – скалярно на третий. Такое произведение называется смешанным произведением трех векторов (векторно–скалярным произведением).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора 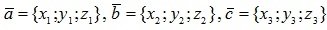заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

(2.35)

Нетрудно показать, что объем параллелепипеда, построенного на векторах 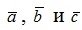как на сторонах, приведенных к общему началу, численно равен модулю смешенного произведения этих векторов .

Объем треугольной пирамиды, построенной на этих же векторах, равен

(2.36)

Пример 2.13. Вершинами пирамиды служат точки 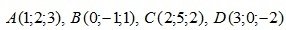. Вычислить объем пирамиды.

Решение. Найдем координаты векторов

. Вычислим смешанное произведение этих векторов: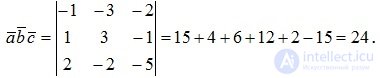

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

Система векторов 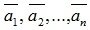называется линейно зависимой, если существуют такие числа 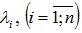, хотя бы одно из которых отлично от нуля, что имеет место равенство

(2.37)

Отсюда всегда можно один из линейно зависимых векторов выразить через линейную комбинацию остальных. Действительно, допустим для определенности, что 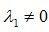. Тогда на это число разделим равенство (2.37), имеем:

получим выражение вектора 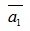через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

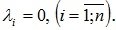В системе векторов 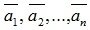число линейно независимых векторов равняется рангу матрицы, которая составлена из координат этих векторов (смотри раздел I.5).

Базисом n – мерного пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

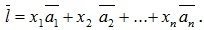
Числа называются координатами вектора в базисе векторов .

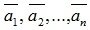Линейное пространство называется конечномерным и имеет размерность n, если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Например, в трехмерном пространстве существует базис единичных орт 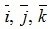такой, что любое расширение этой системы линейно независимых векторов, то есть каждый вектор трехмерного пространства, приводит к линейной зависимости векторов (является линейной комбинацией орт 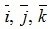): 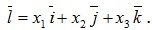Коэффициенты {x1, x2, x3} такого разложения вектора по ортам 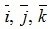являются координатами вектора в трехмерном пространстве.

Я что-то не договорил про векторы в пространстве, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое векторы в пространстве, векторы в пространстве и действия над ними и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия