Шар - понятие , свойства кратко

Привет, сегодня поговорим про шар, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое шар , настоятельно рекомендую прочитать все из категории Стереометрия.

шар ом называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.

Граница шара называется шаровой поверхностью, или сферой. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром

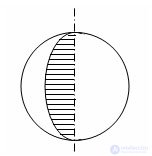
Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

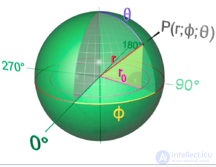
Шар

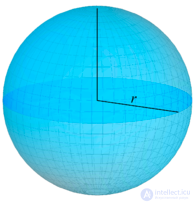
Сфера - поверхность шара радиуса r

ИЗ ИСТОРИИ ВОЗНИКНОВЕНИЯ

Шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова « сфайра» - мяч. При этом слово « шар» образовалось от перехода согласных сф в ш. В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом. В древности сфера была в большом почете. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. Сфера всегда широко применялось в различных областях науки и техники.

Связанные определения

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами. Площадь этих сечений вычисляется по формуле πR².

Основные геометрические формулы

Площадь поверхности и объем шара радиуса (и диаметром ) определяются формулами:

• 

• 

• 

• 

Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии.

Определения

Пусть дано метрическое пространство . Тогда

• Шаром (или открытым шаром) с центром в точке и радиусом называется множество

• Замкнутым шаром с центром в и радиусом называется множество

Замечания[

Шар радиуса с центром также называют -окрестностью точки .

Свойства

• Шар является открытым множеством в топологии, порожденной метрикой .
• Замкнутый шар — замкнутым множеством в топологии, порожденной метрикой .
• По определению такой топологии открытые шары с центрами в любой точке являют собой ее базу.
• Очевидно, . Об этом говорит сайт https://intellect.icu . Однако, вообще говоря, замыкание открытого шара может не совпадать с замкнутым шаром:
  • Например: пусть — дискретное метрическое пространство, и состоит из более, чем двух точек. Тогда для любого имеем:

Объем

Объем n-мерного шара радиуса R в n-мерном евклидовом пространстве:

где Γ — это эйлеровская гамма-функция (которая является расширением факториала на поле действительных и комплексных чисел). Используя частные представления гамма-функции для целых и полуцелых значений, можно получить формулы объема n-мерного шара, которые не требуют гамма-функции:

,

.

Знаком !! здесь обозначен двойной факториал.

Эти формулы также можно свести в одну общую:

.

Обратная функция для выражения зависимости радиуса от объема:

.

Эта формула также может быть разделена на две: для пространств с четным и нечетным количеством размерностей, используя факториал и двойной факториал вместо гамма-функции:

,

.

Рекурсия

Формулу объема также можно выразить в виде рекурсивной функции. Эти формулы могут быть доказаны непосредственно или выведены из основной формулы, представленной выше. Проще всего выразить объем n-мерного шара через объем шара размерности (при условии, что они имеют одинаковый радиус):

.

Также существует формула объема n-мерного шара в зависимости от объема (n−1)-мерного шара того же радиуса:

.

То же без гамма-функции:

Пространства младших размерностей

Формулы объема для некоторых пространств младших размерностей:

Кол-во измерений	Объем шара радиуса R	Радиус шара объема V
1
2
3
4
5
6
7
8
9
10

Пространства старших размерностей

При стремлении количества размерностей к бесконечности объем шара единичного радиуса стремится к нулю. Это может быть выведено из рекурсивного представления формулы объема.

Примеры

• Пусть — евклидово пространство с обычным Евклидовым расстоянием. Тогда

• если (пространство — прямая), то

— открытый и замкнутый отрезок соответственно.

• если (пространство — плоскость), то

  

  

— открытый и замкнутый диск соответственно.

• если , то

  

  

— открытый и замкнутый стереометрический шар соответственно.

• В иных метриках шар может иметь иную геометрическую форму. Например, определим в евклидовом пространстве метрику следующим образом:

  

Тогда

• если , то — это открытый квадрат с центром в точке и сторонами длины , расположенными по диагонали к координатным осям.
• если , то — это открытый трехмерный октаэдр.

Вау!! 😲 Ты еще не читал? Это зря!

• Шаровой слой
• Гиперсфера
• Сферический слой
• сфера ,

Я что-то не договорил про шар, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое шар и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия

Из статьи мы узнали кратко, но содержательно про шар