Лекция
Привет, сегодня поговорим про угол между прямой, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое угол между прямой, плоскостью– определение ы нахождения , настоятельно рекомендую прочитать все из категории Стереометрия.
|
Начнем эту статью с определения угла между прямой и плоскостью. После этого покажем, как находится угол между прямой и плоскостью методом координат, подробно разберем решения характерных примеров и задач.
Прежде чем говорить об определении угла между прямой и плоскостью, рекомендуем освежить в памяти понятие прямой линии в пространстве и понятие плоскости.
Чтобы определить угол между прямой и плоскостью нам потребуется несколько вспомогательных определений. Дадим эти определения.
Определение.
Прямая и плоскость пересекаются, если они имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости.
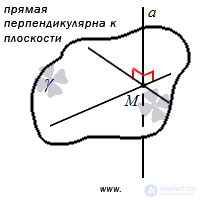
При этом прямая, которая пересекает плоскость, может быть перпендикулярна к этой плоскости.
Определение.
Прямая перпендикулярна к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Определение.
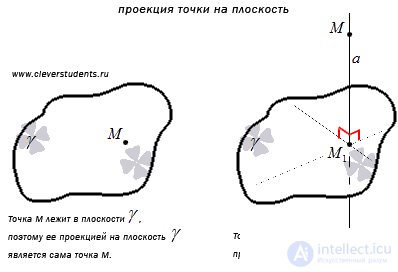
Проекцией точки М на плоскость 
называется либо сама точка М, если М лежит в плоскости , либо точка пересечения плоскости и прямой, перпендикулярной к плоскости и проходящей через точку М, если точка М не лежит в плоскости .
Определение.
Проекцией прямой a на плоскость называют множество проекций всех точек прямой a на плоскость .
Очевидно, что проекцией прямой, перпендикулярной к плоскости , на плоскость является их точка пересечения. Также достаточно очевидно, что проекцией прямой a, которая пересекает плоскость и не перпендикулярна к этой плоскости, на плоскость является прямая линия, лежащая в плоскости и проходящая через точку пересечения прямой a и плоскости .
Теперь нам достаточно сведений, чтобы дать определение угла между прямой и плоскостью.
Определение.
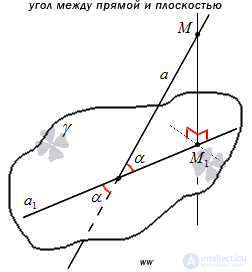
Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость.
Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми: самой прямой и ее проекцией на плоскость. Об этом говорит сайт https://intellect.icu . Следовательно, угол между прямой и плоскостью есть острый угол.
Угол между перпендикулярными прямой и плоскостью считают равным 
, а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным 
.
Условия задач, в которых приходится отыскивать угол между прямой и плоскостью, достаточно разнообразны. В зависимости от исходных данных, приходится подбирать соответствующий метод решения. Часто справиться с задачей нахождения угла между прямой и плоскостью помогают признаки равенства или подобия фигур, теорема косинусов и определения синуса, косинуса и тангенса угла. Также можно найти угол между прямой и плоскостью методом координат. Остановимся на нем подробнее.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , в ней задана прямая a, которая пересекает плоскость в точке M и не перпендикулярна плоскости , и требуется найти угол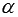 
между прямой a и плоскостью .
Начнем с начальных данных, от которых мы будем отталкиваться при определении угла между прямой и плоскостью методом координат.
Прямой a в заданной прямоугольной системе координат Oxyz соответствуют некоторыеуравнения прямой в пространстве и направляющий вектор прямой в пространстве, а плоскости - уравнение плоскости некоторого вида и нормальный вектор плоскости. Пусть 
- направляющий вектор прямой a, 
- нормальный вектор плоскости . Итак, будем считать, что нам известны координаты направляющего вектора прямой a и координаты нормального вектора плоскости (если известны уравнения прямой aи плоскости , то координаты векторов 
и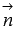 
определяются по этим уравнениям).
Осталось получить формулу, которая позволят вычислять угол между прямой и плоскостью по известным координатам направляющего вектора прямой и нормального вектора плоскости.
Отложим векторы и 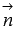от точки пересечения прямой a и плоскости . В зависимости от координат векторов и 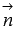возможны четыре варианта расположения этих векторов относительно заданных прямой и плоскости. Изобразим их на чертеже.
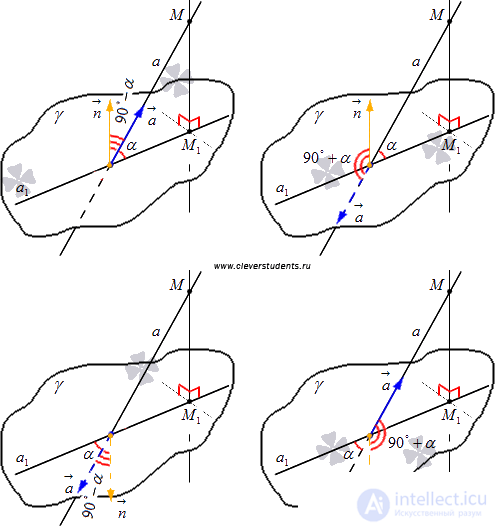
Очевидно, если угол между векторами и 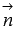(обозначим его 
) острый, то он дополняет искомый угол 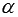между прямой и плоскостью до прямого угла, то есть, 
. Если же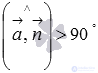 
, то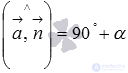 
.
Так как косинусы равных углов равны, то последние равенства можно записать следующим образом: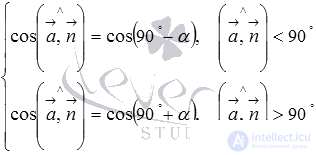
Формулы приведения приводят нас к равенствам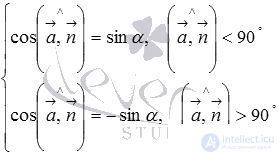 
, которые после преобразований принимают вид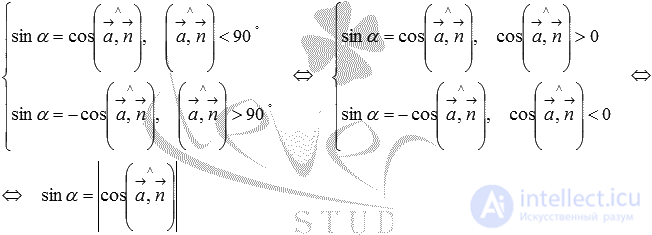
То есть, синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором плоскости.
В разделе нахождение угла между двумя векторами мы выяснили, что угол между векторами равен отношению скалярного произведения векторов и произведения длин этих векторов, тогда для вычисления синуса угла между прямой и плоскостью справедлива формула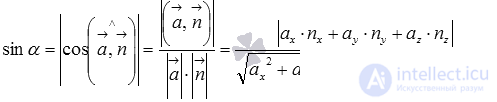 
.
Следовательно, формула для вычисления угла между прямой и плоскостью по координатам направляющего вектора прямой и нормального вектора плоскости имеет вид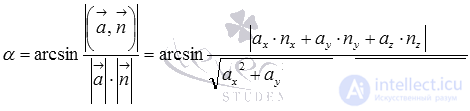 
.
Основное тригонометрическое тождество позволяет найти косинус угла при известном синусе. Так как угол между прямой и плоскостью острый, то косинус этого угла является положительным числом и вычисляется по формуле 
.
Теперь мы можем находить синус угла, косинус угла и сам угол между прямой и плоскостью по полученным формулам. Решим несколько характерных примеров.
Пример.
Найдите угол, синус и косинус угла между прямой 
и плоскостью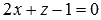 
.
Решение.
Канонические уравнения прямой в пространстве позволяют сразу получить координаты направляющего вектора – их дают числа в знаменателях дробей. То есть, 
- направляющий вектор прямой .
Общее уравнение плоскости содержит в себе координаты нормального вектора плоскости в виде коэффициентов при переменных x, y и z. То есть, нормальным вектором плоскости 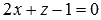является вектор 
.
Подставляем координаты векторов и 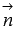в формулу для вычисления синуса угла между прямой и плоскостью:
Тогда 
и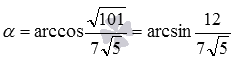 
.
Ответ:
Пример.
На векторах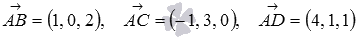 
построена пирамида. Найдите угол между прямой AD и плоскостью ABC.
Решение.
Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямой AD является вектор 
.
Нормальный вектор 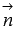плоскости АВС перпендикулярен и вектору 
и вектору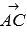 
, то есть, в качестве нормального вектора плоскости АВС можно взять векторное произведение векторов и :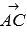
Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью:
Ответ:
Я что-то не договорил про угол между прямой, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое угол между прямой, плоскостью– определение ы нахождения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Из статьи мы узнали кратко, но содержательно про угол между прямой
угол между прямой и плоскостью" /> 
Комментарии