Лекция
Привет, сегодня поговорим про подобие пространственных фигур, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое подобие пространственных фигур , настоятельно рекомендую прочитать все из категории Стереометрия.
Преобразование фигуры F называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же количество раз, т.е. для любых двух точек X и Y фигуры F и точек X`, Y` фигуры F`, в которые они переходят X`Y` = k * XY.
Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
Преобразование подобия в пространстве определяется так же, как и на плоскости. А именно: преобразование фигуры F называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз, т. е. для любых двух точек X и У фигуры F и точек X', У фигуры F', в которые они переходят, X'Y' = k.XY.
Так же как и на плоскости, преобразование подобия в пространстве переводит прямые в прямые, полупрямые в полупрямые, отрезоки в отрезки и сохраняет углы между полупрямыми. Такими же рассуждениями, как в п. 157, доказывается, что преобразование подобия переводит плоскости в плоскости. Так же как и на плоскости, две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
Простейшим преобразованием подобия в пространстве является гомотетия. Об этом говорит сайт https://intellect.icu . Так же как и на плоскости, гомотетия относительно центра О с коэффициентом гомотетии k — это преобразование, которое переводит произвольную точку X в точку X' луча ОХ, такую, что OX' = k.OX.
Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя при k=1).
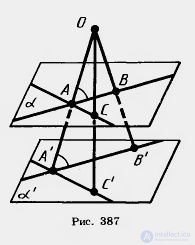
Действительно, пусть О — центр гомотетии и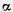 
— любая плоскость, не проходящая через точку О (рис. 387). Возьмем любую прямую АВ в плоскости 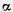. Преобразование гомотетии переводит точку А в точку А' на луче OA, а точку В в точку В' на луче ОВ, причем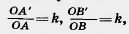 
k — коэффициент гомотетии. Отсюда следует подобие треугольников АОВ и А'ОВ'. Из подобия треугольников следует равенство соответственных углов ОАВ и ОА'В', а значит, параллельность прямых АВ и А'В'.
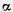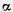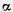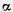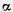Возьмем теперь другую прямую АС в плоскости . Она при гомотетии перейдет в параллельную прямую А'С'. При рассматриваемой гомотетии плоскость перейдет в плоскость ',' проходящую через прямые А'В', А'С. Так как А'В'llАВ и А'С'llАС, то по теореме 16.4 плоскости и ' параллельны, что и требовалось доказать.
Я что-то не договорил про подобие пространственных фигур, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое подобие пространственных фигур и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Из статьи мы узнали кратко, но содержательно про подобие пространственных фигур
Комментарии