Лекция
Привет, сегодня поговорим про угол между двумя пересекающимися плоскостями – определение ы нахождения , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое угол между двумя пересекающимися плоскостями – определение ы нахождения , настоятельно рекомендую прочитать все из категории Стереометрия.
Теорема
Угол между плоскостями не зависит от выбора секущей плоскости. 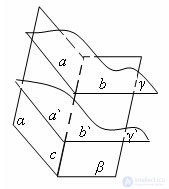
Доказательство.
Пусть есть две плоскости α и β, которые пересекаются по прямой с. проведем плоскость γ перпендикулярно прямой с. Тогда плоскость γ пересечет плоскости α и β по прямым a и b соответственно. Угол между плоскостями α и β равен углу между прямыми a и b.
Возьмем другую секущую плоскость γ`, перпендикулярную с. Тогда плоскость γ` пересечет плоскости α и β по прямым a` и b` соответственно.
При параллельном переносе точка пересечения плоскости γ с прямой с перейдет в точку пересечения плоскости γ` с прямой с. при этом по свойству параллельного переноса прямая a перейдет в прямую a`, b – в прямую b`. следовательно углы между прямыми a и b, a` и b` равны. Теорема доказана.
Эта статья посвящена углу между плоскостями и его нахождению. Сначала приведено определение угла между двумя плоскостями и дана графическая иллюстрация. После этого разобран принцип нахождения угла между двумя пересекающимися плоскостями методом координат, получена формула, позволяющая вычислять угол между пересекающимися плоскостями по известным координатам нормальных векторов этих плоскостей. В заключении показаны подробные решения характерных задач.
При изложении материала мы будем использовать определения и понятия, данные в статьяхплоскость в пространстве и прямая в пространстве.
Приведем рассуждения, которые позволят постепенно подойти к определению угла между двумя пересекающимися плоскостями.
Пусть нам даны две пересекающиеся плоскости  и
и  . Эти плоскости пересекаются по прямой, которую обозначим буквой c. Построим плоскость
. Эти плоскости пересекаются по прямой, которую обозначим буквой c. Построим плоскость  , проходящую через точку Мпрямой c и перпендикулярную к прямой c. При этом плоскость
, проходящую через точку Мпрямой c и перпендикулярную к прямой c. При этом плоскость  будет пересекать плоскости
будет пересекать плоскости  и
и  . Обозначим прямую, по которой пересекаются плоскости
. Обозначим прямую, по которой пересекаются плоскости  и
и  как a, а прямую, по которой пересекаются плоскости
как a, а прямую, по которой пересекаются плоскости  и
и 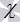 как b. Очевидно, прямые a и b пересекаются в точкеМ.
как b. Очевидно, прямые a и b пересекаются в точкеМ.
Легко показать, что угол между пересекающимися прямыми a и b не зависит от расположения точки М на прямой c, через которую проходит плоскость  .
.
Построим плоскость  , перпендикулярную к прямой c и отличную от плоскости
, перпендикулярную к прямой c и отличную от плоскости 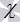 . Плоскость
. Плоскость 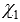 пересекают плоскости
пересекают плоскости  и
и  по прямым, которые обозначим a1 и b1 соответственно.
по прямым, которые обозначим a1 и b1 соответственно.
Из способа построения плоскостей 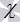 и
и 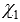 следует, что прямые a и b перпендикулярны прямой c, и прямые a1 и b1 перпендикулярны прямой c. Так как прямые a и a1 лежат в одной плоскости
следует, что прямые a и b перпендикулярны прямой c, и прямые a1 и b1 перпендикулярны прямой c. Так как прямые a и a1 лежат в одной плоскости  и перпендикулярны прямой c, то они параллельны. Аналогично, прямые b и b1лежат в одной плоскости
и перпендикулярны прямой c, то они параллельны. Аналогично, прямые b и b1лежат в одной плоскости  и перпендикулярны прямой c, следовательно, они параллельны. Таким образом, можно выполнить параллельный перенос плоскости
и перпендикулярны прямой c, следовательно, они параллельны. Таким образом, можно выполнить параллельный перенос плоскости 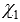 на плоскость
на плоскость 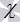 , при котором прямая a1 совпадет с прямой a, а прямая b с прямой b1. Следовательно, угол между двумя пересекающимися прямыми a1 и b1 равен углу между пересекающимися прямыми a и b.
, при котором прямая a1 совпадет с прямой a, а прямая b с прямой b1. Следовательно, угол между двумя пересекающимися прямыми a1 и b1 равен углу между пересекающимися прямыми a и b.
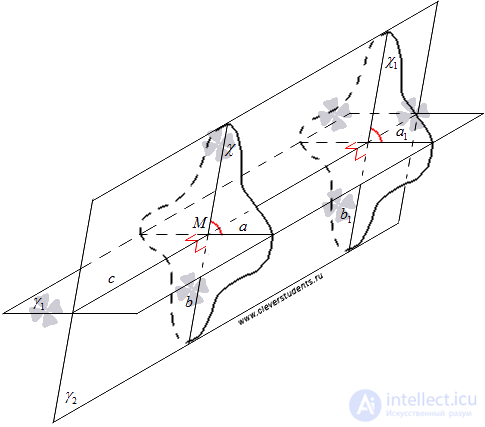
Этим доказано, что угол между пересекающимися прямыми a и b, лежащими в пересекающихся плоскостях  и
и  , не зависит от выбора точки M, через которую проходит плоскость
, не зависит от выбора точки M, через которую проходит плоскость 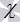 . Поэтому, логично этот угол принять за угол между двумя пересекающимися плоскостями.
. Поэтому, логично этот угол принять за угол между двумя пересекающимися плоскостями.
Теперь можно озвучить определение угла между двумя пересекающимися плоскостями  и
и  .
.
Определение.
Угол между двумя пересекающимися по прямой c плоскостями  и
и  – это угол между двумя пересекающимися прямыми a и b, по которым плоскости
– это угол между двумя пересекающимися прямыми a и b, по которым плоскости  и
и  пересекаются с плоскостью
пересекаются с плоскостью 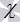 , перпендикулярной к прямой c.
, перпендикулярной к прямой c.
Определение угла между двумя плоскостями можно дать немного иначе. Если на прямой с, по которой пересекаются плоскости  и
и  , отметить точку М и через нее провести прямые а и b, перпендикулярные прямой c и лежащие в плоскостях
, отметить точку М и через нее провести прямые а и b, перпендикулярные прямой c и лежащие в плоскостях  и
и  соответственно, то угол между прямыми а и b представляет собой угол между плоскостями
соответственно, то угол между прямыми а и b представляет собой угол между плоскостями  и
и  . Об этом говорит сайт https://intellect.icu . Обычно на практике выполняют именно такие построения, чтобы получить угол между плоскостями.
. Об этом говорит сайт https://intellect.icu . Обычно на практике выполняют именно такие построения, чтобы получить угол между плоскостями.
Так как угол между пересекающимися прямыми не превосходит 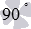 , то из озвученного определения следует, что градусная мера угла между двумя пересекающимися плоскостями выражается действительным числом из интервала
, то из озвученного определения следует, что градусная мера угла между двумя пересекающимися плоскостями выражается действительным числом из интервала 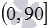 . При этом, пересекающиеся плоскости называют перпендикулярными, если угол между ними равен девяноста градусам. Угол между параллельными плоскостями либо не определяют совсем, либо считают его равным нулю.
. При этом, пересекающиеся плоскости называют перпендикулярными, если угол между ними равен девяноста градусам. Угол между параллельными плоскостями либо не определяют совсем, либо считают его равным нулю.
Обычно при нахождении угла между двумя пересекающимися плоскостями сначала приходится выполнять дополнительные построения, чтобы увидеть пересекающиеся прямые, угол между которыми равен искомому углу, и после этого связывать этот угол с исходными данными при помощи признаков равенства, признаков подобия, теоремы косинусов или определений синуса, косинуса и тангенса угла. В курсе геометрии средней школы встречаются подобные задачи.
Для примера приведем решение задачи С2 из ЕГЭ по математике за 2012 год (условие намерено изменено, но это не влияет на принцип решения). В ней как раз нужно было найти угол между двумя пересекающимися плоскостями.
Пример.
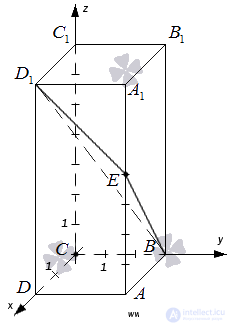
Дан прямоугольный параллелепипед АВСDA1B1C1D1, в котором АВ=3, AD=2, АА1=7 и точка E делит сторону АА1 в отношении 4 к 3, считая от точки А. Найдите угол между плоскостями АВС и ВЕD1.
Решение.
Для начала сделаем чертеж.

Выполним дополнительные построения, чтобы «увидеть» угол между плоскостями.
Для начала определим прямую линию, по которой пересекаются плоскости АВС и BED1. Точка В – это одна из их общих точек. Найдем вторую общую точку этих плоскостей. Прямые DA и D1E лежат в одной плоскости АDD1, причем они не параллельны, а, значит, пересекаются. С другой стороны, прямая DA лежит в плоскости АВС, а прямаяD1E – в плоскости BED1, следовательно, точка пересечения прямых DA и D1E будет общей точкой плоскостей АВС и BED1. Итак, продолжим прямые DA и D1E до их пересечения, обозначим точку их пересечения буквой F. Тогда BF – прямая, по которой пересекаются плоскости АВС и BED1.
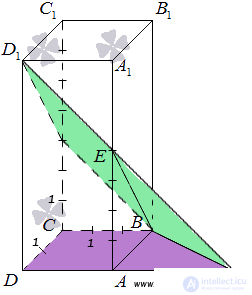
Осталось построить две прямые, лежащие в плоскостях АВС и BED1 соответственно, проходящие через одну точку на прямой BF и перпендикулярные прямой BF, - угол между этими прямыми по определению будет равен искомому углу между плоскостямиАВС и BED1. Сделаем это.
Точка А является проекцией точки Е на плоскость АВС. Проведем прямую, пересекающую под прямым углом прямую ВF в точке М. Тогда прямая АМ является проекцией прямой ЕМ на плоскость АВС, и по теореме о трех перпендикулярах 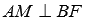 .
.

Таким образом, искомый угол между плоскостями АВС и BED1 равен 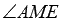 .
.
Синус, косинус или тангенс этого угла (а значит и сам угол) мы можем определить из прямоугольного треугольника АЕМ, если будем знать длины двух его сторон. Из условия легко найти длину АЕ: так как точка Е делит сторону АА1 в отношении 4 к 3, считая от точки А, а длина стороны АА1 равна 7, то АЕ=4. Найдем еще длину АМ.
Для этого рассмотрим прямоугольный треугольник АВF с прямым углом А, где АМявляется высотой. По условию АВ=2. Длину стороны АF мы можем найти из подобия прямоугольных треугольников DD1F и AEF: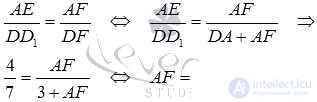
По теореме Пифагора из треугольника АВF находим 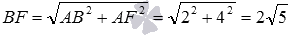 . Длину АМ найдем через площадь треугольникаАBF: c одной стороны площадь треугольника АВF равна
. Длину АМ найдем через площадь треугольникаАBF: c одной стороны площадь треугольника АВF равна 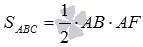 , с другой стороны
, с другой стороны 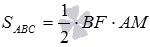 , откуда
, откуда 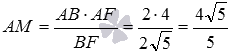 .
.
Таким образом, из прямоугольного треугольника АЕМ имеем 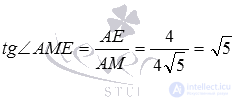 .
.
Тогда искомый угол между плоскостями АВС и BED1 равен 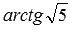 (заметим, что
(заметим, что  ).
).
Ответ:
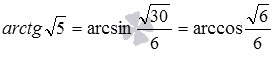
В некоторых случаях для нахождения угла между двумя пересекающимися плоскостями удобно задать прямоугольную систему координат Oxyz и воспользоваться методом координат. На нем и остановимся.
Поставим задачу: найти угол между двумя пересекающимися плоскостями  и
и  . Обозначим искомый угол как
. Обозначим искомый угол как 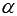 .
.
Будем считать, что в заданной прямоугольной системе координат Oxyz нам известны координаты нормальных векторов пересекающихся плоскостей  и
и  или имеется возможность их найти. Пусть
или имеется возможность их найти. Пусть 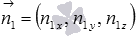 - нормальный вектор плоскости
- нормальный вектор плоскости  , а
, а 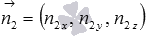 - нормальный вектор плоскости
- нормальный вектор плоскости  . Покажем, как найти угол между пересекающимися плоскостями
. Покажем, как найти угол между пересекающимися плоскостями  и
и  через координаты нормальных векторов этих плоскостей.
через координаты нормальных векторов этих плоскостей.
Обозначим прямую, по которой пересекаются плоскости  и
и  , как c. Через точку М на прямой c проведем плоскость
, как c. Через точку М на прямой c проведем плоскость 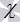 , перпендикулярную к прямой c. Плоскость
, перпендикулярную к прямой c. Плоскость 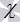 пересекает плоскости
пересекает плоскости  и
и  по прямым a и b соответственно, прямые a и b пересекаются в точке М. По определению угол между пересекающимися плоскостями
по прямым a и b соответственно, прямые a и b пересекаются в точке М. По определению угол между пересекающимися плоскостями  и
и  равен углу между пересекающимися прямыми a и b.
равен углу между пересекающимися прямыми a и b.
Отложим от точки М в плоскости 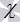 нормальные векторы
нормальные векторы 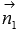 и
и 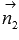 плоскостей
плоскостей  и
и  . При этом вектор
. При этом вектор 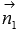 лежит на прямой, которая перпендикулярна прямой a, а вектор
лежит на прямой, которая перпендикулярна прямой a, а вектор 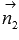 - на прямой, которая перпендикулярна прямой b. Таким образом, в плоскости
- на прямой, которая перпендикулярна прямой b. Таким образом, в плоскости 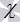 вектор
вектор 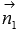 - нормальный вектор прямой a,
- нормальный вектор прямой a, 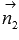 - нормальный вектор прямой b.
- нормальный вектор прямой b.
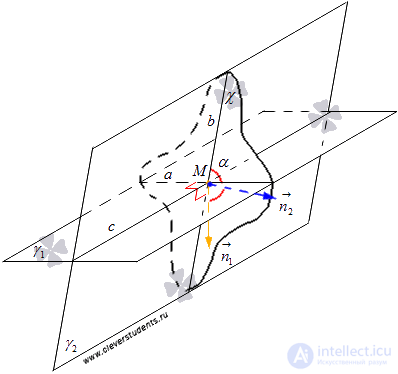
В статье нахождение угла между пересекающимися прямыми мы получили формулу, которая позволяет вычислять косинус угла между пересекающимися прямыми по координатам нормальных векторов. Таким образом, косинус угла между прямыми a и b, а, следовательно, икосинус угла между пересекающимися плоскостями  и
и  находится по формуле
находится по формуле 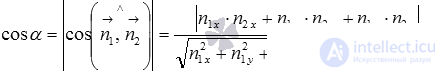 , где
, где 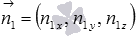 и
и 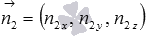 – нормальные векторы плоскостей
– нормальные векторы плоскостей  и
и  соответственно. Тогда угол между пересекающимися плоскостями вычисляется как
соответственно. Тогда угол между пересекающимися плоскостями вычисляется как 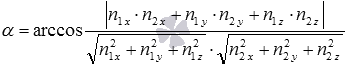 .
.
Решим предыдущий пример методом координат.
Пример.
Дан прямоугольный параллелепипед АВСDA1B1C1D1, в котором АВ=3, AD=2, АА1=7 и точка E делит сторону АА1 в отношении 4 к 3, считая от точки А. Найдите угол между плоскостями АВС и ВЕD1.
Решение.
Так как стороны прямоугольного параллелепипеда при одной вершине попарно перпендикулярны, то удобно ввести прямоугольную систему координат Oxyz так: начало совместить с вершиной С, а координатные оси Ox, Oy и Oz направить по сторонам CD, CB и CC1 соответственно.
Угол между плоскостями АВС и BED1 может быть найден через координаты нормальных векторов этих плоскостей по формуле 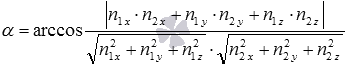 , где
, где 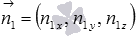 и
и 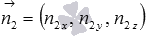 – нормальные векторы плоскостей АВС иBED1 соответственно. Определим координаты нормальных векторов.
– нормальные векторы плоскостей АВС иBED1 соответственно. Определим координаты нормальных векторов.
Так как плоскость АВС совпадает с координатной плоскостью Oxy, то ее нормальным вектором является координатный вектор 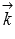 , то есть,
, то есть,  .
.
В качестве нормального вектора плоскости BED1 можно принять векторное произведение векторов 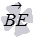 и
и 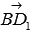 , в свою очередь координаты векторов
, в свою очередь координаты векторов 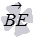 и
и 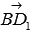 можно найти через координаты точек В, Е и D1 (о чем написано в статье координаты вектора через координаты точек его начала и конца), а координаты точек В, Е и D1 во введенной системе координат определим из условия задачи.
можно найти через координаты точек В, Е и D1 (о чем написано в статье координаты вектора через координаты точек его начала и конца), а координаты точек В, Е и D1 во введенной системе координат определим из условия задачи.
Очевидно, 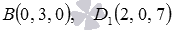 . Так как
. Так как 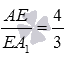 , то по координатам точек
, то по координатам точек  находим
находим 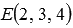 (при необходимости смотрите статьюделение отрезка в заданном отношении). Тогда
(при необходимости смотрите статьюделение отрезка в заданном отношении). Тогда  и
и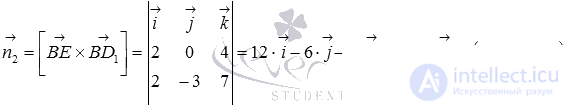
Осталось подставить найденные координаты в формулу для вычислений угла между плоскостями: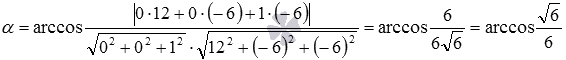
Как видите, метод координат дал такой же результат.
Ответ:
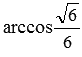
В заключении разберем решение примера, в котором нужно найти угол между пересекающимися плоскостями по известным уравнениям этих плоскостей.
Пример.
Найдите синус угла, косинус угла и сам угол между двумя пересекающимися плоскостями, определенными в прямоугольной системе координат Oxyz уравнениями 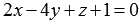 и
и 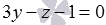 .
.
Решение.
Когда мы изучали общее уравнение прямой вида 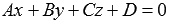 , то выяснили, что коэффициенты А, В и С представляют собой соответствующие координаты нормального вектора плоскости. Таким образом,
, то выяснили, что коэффициенты А, В и С представляют собой соответствующие координаты нормального вектора плоскости. Таким образом, 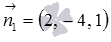 и
и 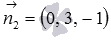 - нормальные векторы плоскостей
- нормальные векторы плоскостей 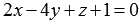 и
и 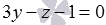 соответственно.
соответственно.
Подставляем координаты нормальных векторов плоскостей в формулу для вычисления угла между двумя пересекающимися плоскостями: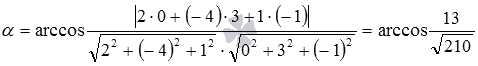
Тогда 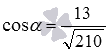 . Так как угол между двумя пересекающимися плоскостями не тупой, то с помощью основного тригонометрического тождества находим синус угла:
. Так как угол между двумя пересекающимися плоскостями не тупой, то с помощью основного тригонометрического тождества находим синус угла:  .
.
Ответ:
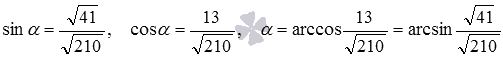
Я что-то не договорил про угол между двумя пересекающимися плоскостями – определение ы нахождения , тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое угол между двумя пересекающимися плоскостями – определение ы нахождения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия