Лекция
Привет, сегодня поговорим про многогранники, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое многогранники, классификация многогранников, платоновы тела, изоэдры , изогоны, параллелоэдры, кристаллографические многогранники , настоятельно рекомендую прочитать все из категории Стереометрия.
Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Многогранник или полиэдр — обычно замкнутая поверхность, составленная из многоугольников, но иногда так же называют тело, ограниченное этой поверхностью.
Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины –вершинами многогранника.
Простейшие
многогранники : куб, призма, пирамида.
Многогранник, точнее трехмерный многогранник — совокупность конечного числа плоских многоугольников в трехмерном евклидовом пространстве, такая, что:
Эти многоугольники называются гранями, их стороны — ребрами, а их вершины — вершинами многогранника .
Простейшим примером многогранника является выпуклый многогранник, то есть граница такого ограниченного подмножества евклидова пространства, которое является пересечением конечного числа полупространств.
Приведенное определение многогранника получает различный смысл в зависимости от того, как определить многоугольник, для которого возможны следующие два варианта:
В первом случае мы получаем понятие звездчатый многогранник. Во втором — многогранник есть поверхность, составленная из многоугольных кусков. Если эта поверхность сама себя не пересекает, то она есть полная поверхность некоторого геометрического тела, которое также называется многогранником. Отсюда возникает третье определение многогранника, как самого геометрического тела.
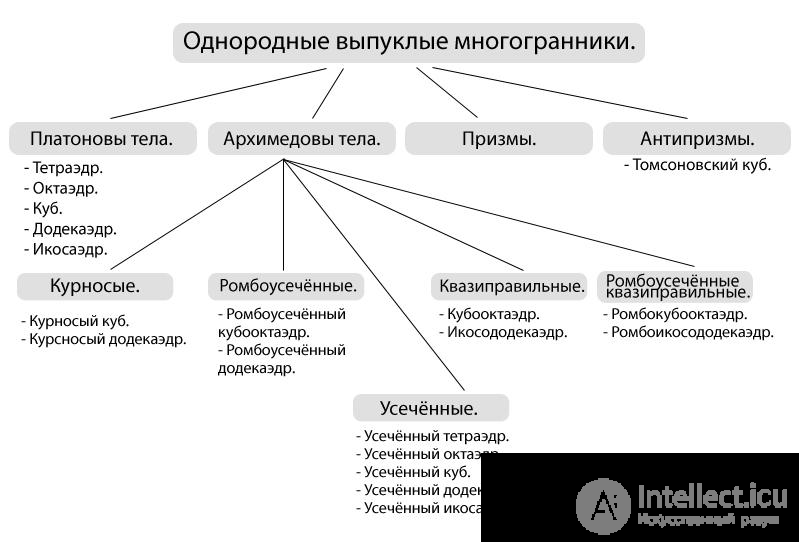
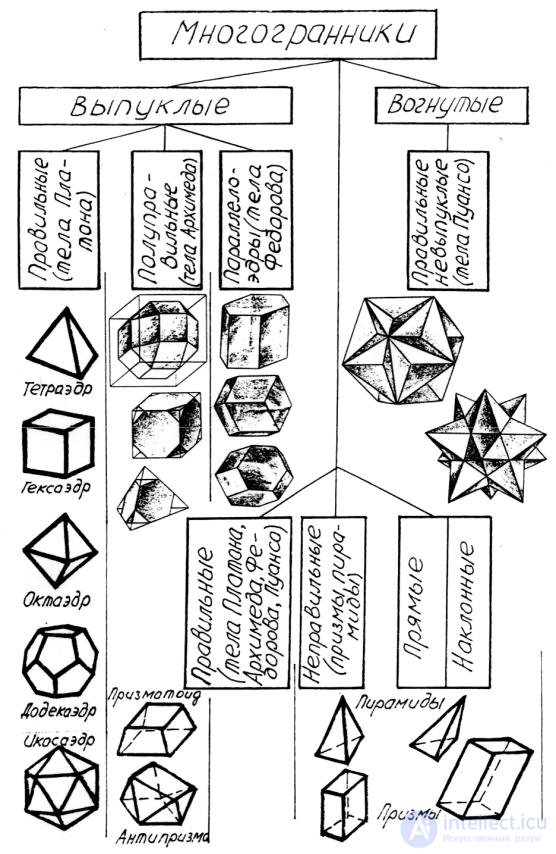
Рисунок 1 – классификация многогранников

Рис. 2. Многогранники: правильные выпуклые многогранники (тела Платона) – 1–5; правильные невыпуклые многогранники (тела Пуансо) – 6–9; полуправильные выпуклые многогранники (тела Архимеда) – 10–23; п..
Существование именно пяти правильных М. было доказано Евклидом. Они – правильные тетраэдр, куб, октаэдр, додекаэдр и икосаэдр (см. рис. 2, 1–5).
Изоэдром (изогоном) называется такой выпуклый М., что группа его поворотов (1-го и 2-го родов, см. Движение) вокруг центра тяжести переводит любую его грань (вершину) в любую другую его грань (вершину). Об этом говорит сайт https://intellect.icu . Каждому изоэдру (изогону) соответствует дуальный изогон (изоэдр). Если М. одновременно и изогон и изоэдр, то он – правильный М. Комбинаторно разл. изоэдров (изогонов) имеется 13 спец. типов и две бесконечные серии (призмы и антипризмы). Оказывается, что каждый из этих изоэдров может быть реализован так, что все его грани суть правильные многоугольники. Полученные так М. называются полуправильными (телами Архимеда, см. рис. 2, 10–23; призмой – 24; антипризмой – 25).
(выпуклые М., найденные Е. С. Федоровым, 1881) – М., рассматриваемые как тела, параллельными переносами которых можно заполнить все бесконечное пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой, т. е. образовать разбиение пространства. Таковы, напр., куб или правильная 6-угольная призма. Существует 5 топологически разл. сеток ребер параллелоэдров (см. рис. 2, 26–30). Число их граней – 6, 8, 12, 12, 14. Для того чтобы М. был параллелоэдром, необходимо и достаточно, чтобы он был выпуклым М. одного из 5 указанных топологич. типов и чтобы все грани его имели центры симметрии.
Если параллелоэдры разбиения смежны целыми гранями, разбиение называется нормальным. Центры параллелоэдров такого разбиения образуют решетку, т. е. совокупность всех точек с целыми координатами относительно какой-то (вообще говоря, не прямоугольной) декартовой системы координат. Множество точек пространства, из которых каждая отстоит от некоторой данной точки OO рассматриваемой решетки Λ не дальше, чем от всякой др. точки этой решетки, называется областью Вороного DOΛDOΛ точки OO в решетке Λ. Область DOΛDOΛ является выпуклым М. с центром в точке OO. Совокупность областей Вороного всех точек произвольной решетки образует нормальное разбиение пространства. Произвольное (даже nn-мерное) нормальное разбиение на параллелоэдры, в каждой из вершин которого сходится n+1n+1 параллелоэдр, может быть аффинным преобразованием превращено в разбиение Вороного для некоторой решетки.
Всякое движение, переводящее в себя решетку Λ и оставляющее на месте точку OO, преобразует в себя область DOΛDOΛ и обратно. Существует 7 групп таких движений: кубическая, ромбоэдрическая, квадратная (или тетрагональная), ортогональная (или ромбическая), моноклинная, триклинная и гексагональная.
Каждая из 7 рассмотренных групп имеет подгруппы, всех разл. таких групп и их подгрупп 32; их называют кристаллографич. классами. Если взять плоскость, не проходящую через точку OO, и подвергнуть ее всем поворотам к.-л. кристаллографич. класса, то полученные плоскости ограничивают либо некоторый изоэдр с центром в точке OO, либо бесконечное выпуклое призматич. тело, либо многогранный угол. Полученные тела называются простыми формами кристаллов, в 1-м случае замкнутыми, во 2-м и 3-м – открытыми. Две простые формы считают одинаковыми, если они имеют один и тот же комбинаторный тип, порождены одним и тем же кристаллографич. классом и повороты этого класса одинаковым образом связаны с формой. Существует 30 разл. в этом смысле замкнутых форм и 17 открытых, каждая из них имеет свое название.
Основываясь на первом (указанном в начале статьи) определении М., можно указать еще 4 правильных невыпуклых многогранника (т. н. тела Пуансо, см. рис. 2, 6–9), впервые найденных Л. Пуансо в 1809. Доказательство несуществования др. невыпуклых правильных М. дал О. Коши в 1811.
Можно рассматривать и nn-мерные М., для которых верны некоторые из указанных теорем. Оказывается, что при n=n= 4 существуют 6 выпуклых правильных М., при больших nn их всего 3: обобщение тетраэдра, куба и октаэдра.
ПЛАТОНОВЫ ТЕЛА, или правильные многогранники, имеют в качестве граней правильные многоугольники, причем число граней, примыкающих к каждой вершине, одинаково. Таковы, как показано на рисунке, тетраэдр, куб (или гексаэдр), октаэдр, икосаэдр и додекаэдр. Первое число в скобках указывает, сколько сторон у каждой грани, второе - число граней, примыкающих к каждой вершине.
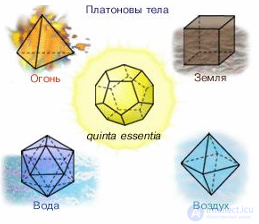
Платон считал, что мир строится из четырех «стихий»: огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырех правильных многогранников.
Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества: твердым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим. Это была одна из первых попыток ввести в науку идею систематизации.
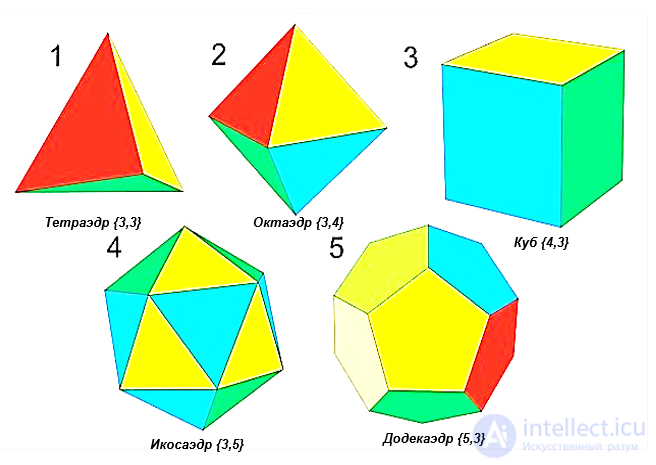
Рисунок Тетраэдр,Октаэдр ,Куб,Икосаэдр,Икосаэдр,Додекаэдр
Таблица 1 - Элементы правильных многогранников
|
Тетраэдр
|
Октаэдр
|
Икосаэдр
|
Гексаэдр (куб)
|
Додекаэдр
|
|
| Количество граней | 4 | 8 | 20 | 6 | 12 |
| количество ребер | 6 | 12 | 30 | 12 | 30 |
| вершин | 4 | 6 | 12 | 8 | 20 |
| Развертки | 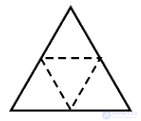 |
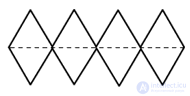 |
 |
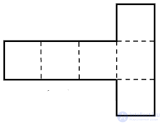 |
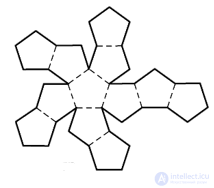 |
Теорема Эйлера Вершины + Грани - Ребра = 2.
Следующий серьезный шаг в науке о многогранниках был сделан в XVIII веке Леонардом Эйлером (1707-1783), который без преувеличения «проверил алгеброй гармонию». Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г. в «Записках Петербургской академии наук», окончательно навела математический порядок в многообразном мире многогранников.
Многогранник с n гранями называют n-гранником. В частности, тетраэдр — четырехгранник, додекаэдр — двенадцатигранник, икосаэдр — двадцатигранник и т. д.
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой его грани.
Для выпуклого многогранника верна теорема Эйлера В + Г − Р = 2, где В — количество вершин многогранника, Г — количество граней, Р — количество ребер.
Я что-то не договорил про многогранники, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое многогранники, классификация многогранников, платоновы тела, изоэдры , изогоны, параллелоэдры, кристаллографические многогранники и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия