Лекция
Привет, сегодня поговорим про угол между скрещивающимися прямыми, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое угол между скрещивающимися прямыми , настоятельно рекомендую прочитать все из категории Стереометрия.
Две пересекающиеся прямые образуют смежные и вертикальные углы. Вертикальные углы равны, а смежные углы дополняют друг друга до 180º. Угловая мера меньшего из них называется углом между прямыми.
Углом между скрещивающимися прямыми называется угол межу пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
В этой статье сначала дадим определение угла между скрещивающимися прямыми и приведем графическую иллюстрацию. Далее ответим на вопрос: «Как найти угол между скрещивающимися прямыми , если известны координаты направляющих векторов этих прямых в прямоугольной системе координат»? В заключении попрактикуемся в нахождении угла между скрещивающимися прямыми при решении примеров и задач.
К определению угла между скрещивающимися прямыми будем подходить постепенно.
Сначала напомним определение скрещивающихся прямых: две прямые в трехмерном пространстве называются скрещивающимися, если они не лежат в одной плоскости. Из этого определения следует, что скрещивающиеся прямые не пересекаются, не параллельны, и, тем более, не совпадают, иначе они обе лежали бы в некоторой плоскости.
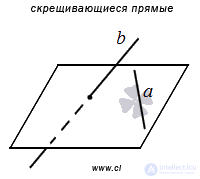
Приведем еще вспомогательные рассуждения.
Пусть в трехмерном пространстве заданы две скрещивающиеся прямые a и b. Построим прямые a1 и b1 так, чтобы они были параллельны скрещивающимся прямым a и bсоответственно и проходили через некоторую точку пространства M1. Таким образом, мы получим две пересекающиеся прямые a1 и b1. Пусть угол между пересекающимися прямыми a1и b1 равен углу  . Теперь построим прямые a2 и b2, параллельные скрещивающимся прямым aи b соответственно, проходящие через точку М2, отличную от точки М1. Угол между пересекающимися прямыми a2 и b2 также будет равен углу
. Теперь построим прямые a2 и b2, параллельные скрещивающимся прямым aи b соответственно, проходящие через точку М2, отличную от точки М1. Угол между пересекающимися прямыми a2 и b2 также будет равен углу  . Это утверждение справедливо, так как прямые a1 и b1 совпадут с прямыми a2 и b2 соответственно, если выполнить параллельный перенос, при котором точка М1 перейдет в точку М2. Таким образом, мера угла между двумя пересекающимися в точке М прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М.
. Это утверждение справедливо, так как прямые a1 и b1 совпадут с прямыми a2 и b2 соответственно, если выполнить параллельный перенос, при котором точка М1 перейдет в точку М2. Таким образом, мера угла между двумя пересекающимися в точке М прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М.
Теперь мы готовы к тому, чтобы дать определение угла между скрещивающимися прямыми.
Определение.
Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Из определения следует, что угол между скрещивающимися прямыми также не будет зависеть от выбора точки M. Поэтому в качестве точки М можно взять любую точку, принадлежащую одной из скрещивающихся прямых.
Приведем иллюстрацию определения угла между скрещивающимися прямыми.
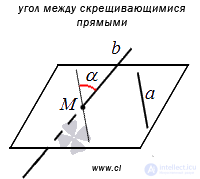
Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.
Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. Об этом говорит сайт https://intellect.icu . То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет теорема косинусов, а иногда к результату приводит определение синуса, косинуса и тангенса угла прямоугольного треугольника.
Однако очень удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат. Именно его и рассмотрим.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz (правда, во многих задачах ее приходится вводить самостоятельно).
Поставим перед собой задачу: найти угол  между скрещивающимися прямыми a и b, которым соответствуют в прямоугольной системе координат Oxyz некоторые уравнения прямой в пространстве.
между скрещивающимися прямыми a и b, которым соответствуют в прямоугольной системе координат Oxyz некоторые уравнения прямой в пространстве.
Решим ее.
Возьмем произвольную точку трехмерного пространства М и будем считать, что через нее проходят прямые a1 и b1, параллельные скрещивающимся прямым a и b соответственно. Тогда искомый угол  между скрещивающимися прямыми a и b равен углу между пересекающимися прямыми a1 и b1 по определению.
между скрещивающимися прямыми a и b равен углу между пересекающимися прямыми a1 и b1 по определению.
Таким образом, нам осталось найти угол между пересекающимися прямыми a1 и b1. Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a1 и b1.
Как же мы их можем получить? А очень просто. Определение направляющего вектора прямойпозволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a1 и b1 можно принять направляющие векторы  и
и 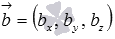 прямых a и b соответственно.
прямых a и b соответственно.
Координаты векторов 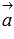 и
и 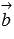 определяются либо по известным из условия уравнениям прямыхa и b (смотрите раздел координаты направляющего вектора прямой), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория разделакоординаты вектора через координаты точек его начала и конца).
определяются либо по известным из условия уравнениям прямыхa и b (смотрите раздел координаты направляющего вектора прямой), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория разделакоординаты вектора через координаты точек его начала и конца).
Итак, угол между двумя скрещивающимися прямыми a и b вычисляется по формуле 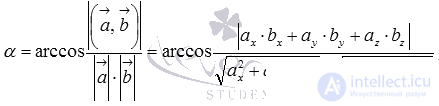 , где
, где  и
и 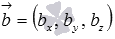 - направляющие векторы прямых a и b соответственно.
- направляющие векторы прямых a и b соответственно.
Формула для нахождения косинуса угла между скрещивающимися прямыми a и bимеет вид 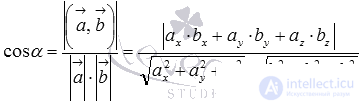 .
.
Основное тригонометрическое тождество позволяет найти синус угла между скрещивающимися прямыми, если известен косинус: 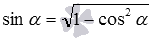 .
.
Осталось разобрать решения примеров.
Пример.
Найдите угол между скрещивающимися прямыми a и b, которые определены в прямоугольной системе координат Oxyz уравнениями  и
и  .
.
Решение.
Канонические уравнения прямой в пространстве позволяют сразу определить координаты направляющего вектор этой прямой – их дают числа в знаменателях дробей, то есть, 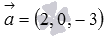 - направляющий вектор прямой
- направляющий вектор прямой  .Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть,
.Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть,  - направляющий вектор прямой
- направляющий вектор прямой  . Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми:
. Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми: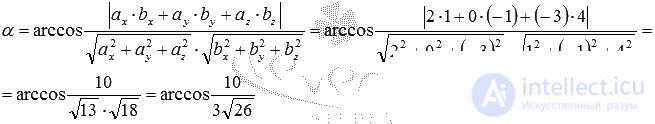
Ответ:
угол между заданными скрещивающимися прямыми равен 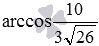 .
.
Пример.
Найдите синус и косинус угла между скрещивающимися прямыми, на которых лежат ребра AD и BC пирамиды АВСD, если известны координаты ее вершин: 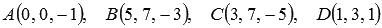 .
.
Решение.
Направляющими векторами скрещивающихся прямых AD и BC являются векторы 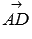 и
и 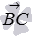 . Вычислим их координаты как разность соответствующих координат точек конца и начала вектора:
. Вычислим их координаты как разность соответствующих координат точек конца и начала вектора: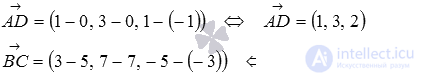
По формуле 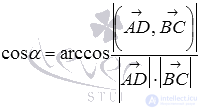 мы можем вычислить косинус угла между указанными скрещивающимися прямыми:
мы можем вычислить косинус угла между указанными скрещивающимися прямыми: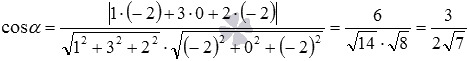
Теперь вычислим синус угла между скрещивающимися прямыми: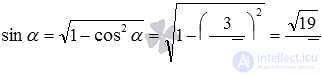
Ответ:
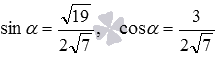
В заключении рассмотрим решение задачи, в которой требуется отыскать угол между скрещивающимися прямыми, а прямоугольную систему координат приходится вводить самостоятельно.
Пример.
Дан прямоугольный параллелепипед ABCDA1B1C1D1, у которого АВ=3, АD=2 и AA1=7единиц. Точка E лежит на ребре АА1 и делит его в отношении 5 к 2 считая от точки А. Найдите угол между скрещивающимися прямыми ВЕ и А1С.
Решение.
Так как ребра прямоугольного параллелепипеда при одной вершине взаимно перпендикулярны, то удобно ввести прямоугольную систему координат, и определить угол между указанными скрещивающимися прямыми методом координат через угол между направляющими векторами этих прямых.
Введем прямоугольную систему координат Oxyz следующим образом: пусть начало координат совпадает с вершиной А, ось Ox совпадает с прямой АD, ось Oy - с прямойАВ, а ось Oz – с прямой АА1.
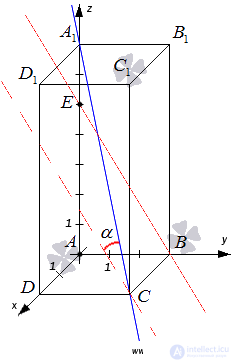
Тогда точка В имеет координаты 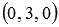 , точка Е -
, точка Е - 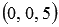 (при необходимости смотрите статью деление отрезка в данном отношении), точка А1 -
(при необходимости смотрите статью деление отрезка в данном отношении), точка А1 - 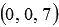 , а точка С -
, а точка С - 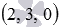 . По координатам этих точек мы можем вычислить координаты векторов
. По координатам этих точек мы можем вычислить координаты векторов 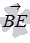 и
и 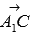 . Имеем
. Имеем 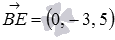 ,
, 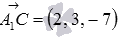 .
.
Осталось применить формулу для нахождения угла между скрещивающимися прямыми по координатам направляющих векторов: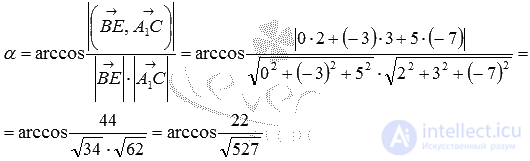
Ответ:
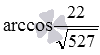
Я что-то не договорил про угол между скрещивающимися прямыми, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое угол между скрещивающимися прямыми и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Из статьи мы узнали кратко, но содержательно про угол между скрещивающимися прямыми
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия