Симметрия шара и симметрия сферы, Симметричность кратко

Привет, сегодня поговорим про симметрия шара, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое симметрия шара, симметрия сферы, симметричность , настоятельно рекомендую прочитать все из категории Стереометрия.

симметричность

Одно из самых важных свойств, которым может обладать фигура — это ее симметричность. Само слово "симметрия" — с греческого может быть переведено как "соразмерность". Симметричная фигура содержит в себе равные и однообразно расположенные части, что придает ей уравновешенность (например, меридианы у фигуры вращения).

Изучая различные фигуры, мы каждый раз будем находить их элементы симметрии, т. е. центры, оси и плоскости различных видов их симметрии.

Не считая самого пространства, сфера и шар — самые симметричные фигуры. В предыдущем пункте мы уже убедились, что сфера и шар обладают вращательной симметрией, т. е. могут быть самосовмещены поворотом вокруг осей, проходящих через их центр. В следующих пунктах мы познакомимся еще с двумя видами их симметрии. Мы будем говорить о симметрии сферы, но все сказанное о ней распространяется на шар.

Симметричность шара

Теорема

Любая диаметральная плоскость шара является его плоскостью. Центр шара является его центром симметрии.



Доказательство

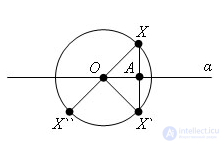
Пусть α - диаметральная плоскость и X - произвольная точка шара. Построим точку X`, симметричную точке X относительно отрезку XX` и пересекается с ним в его середине. Из равенства прямоугольных треугольников OAX и OAX` следует, что OX` = OX.
Так как OX ≤ R, то и OX` ≤ R, т.е. точка, симметричная точке X, принадлежит шару. Первое утверждение теоремы доказано.
Пусть теперь X`` - точка, симметричная точке X относительно центра шара. Тогда OX`` = OX ≤ R, т.е. точка X`` принадлежит шару.

Теорема доказана полностью.

Симметричность сферы

Сфера — центрально симметричная фигура.

О центральной симметрии говорилось в планиметрии.

Рис. Об этом говорит сайт https://intellect.icu . 4.25

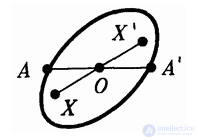
Рис. 4.26

Все сказанное там дословно повторяется в стереометрии. Напомним определения.

Точки А и А называются симметричными относительно точки О, если точка О делит отрезок АА пополам (рис. 4.24). Точка О считается симметричной сама себе (относительно О).

Две фигуры называются симметричными относительно точки О, если они состоят из попарно симметричных точек (рис. 4.25). Это значит, что для каждой точки одной фигуры симметричная ей (относительно О) точка лежит в другой фигуре.

В частности, фигура может быть симметрична сама себе относительно некоторой точки О. Это значит, что для каждой ее точки X точка X, симметричная X относительно О, лежит в ней же. Точка О называется тогда центром симметрии фигуры, а фигура называется центрально симметричной (рис. 4.26).

Сфера симметрична относительно своего центра, т.е. центр сферы является центром симметрии сферы. В самом деле, для каждой точки X сферы с центром О симметричная ей (относительно О) точка лежит на сфере — этой точкой X будет диаметрально противоположная точка (рис. 4.27).

Сфера — зеркально симметричная фигура.

Зеркальная симметрия в пространстве аналогична осевой симметрии на плоскости, но в определениях прямую надо заменить плоскостью.

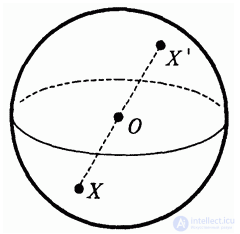
Рис. 4.27

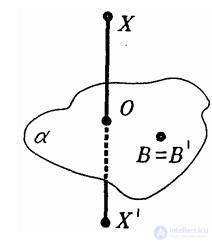
Рис. 4.28

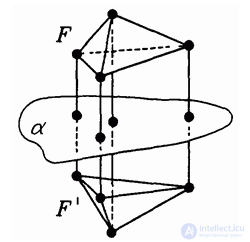
Рис. 4.29

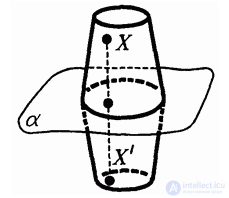
Рис. 4.30

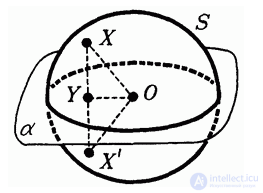
Рис. 4.31

Точки X и X называются симметричными относительно плоскости а, если отрезок XX перпендикулярен плоскости а и делится ею пополам (рис. 4.28). Каждая точка плоскости а считается симметричной сама себе (относительно а).

Две фигуры называются симметричными относительно плоскости а (или зеркально симметричными относительно а), если они состоят из попарно симметричных точек (рис. 4.29). Это значит, что для каждой точки одной фигуры симметричная ей точка (относительно а) лежит в другой фигуре.

В частности, фигура может быть симметрична сама себе относительно некоторой плоскости а. Это значит, что для каждой ее точки X точка X, симметричная X относительно плоскости а, лежит в ней же. Плоскость а называется тогда плоскостью симметрии фигуры, а фигура называется зеркально симметричной (рис. 4.30).

Сфера симметрична относительно любой плоскости, проходящей через ее центр (рис. 4.31). Это означает следующее.

Пусть S — некоторая сфера радиуса R с центром в точке О и а — любая плоскость, проходящая через точку О. Возьмем

любую точку X сферы S, не лежащую в плоскости а Построим симметричную ей относительно а точку X. Для этого опустим из точки X перпендикуляр XY на плоскость а и продолжим его за точку Y на отрезок 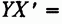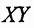. Прямоугольные треугольники OXY и OXY равны (по двум катетам). Поэтому 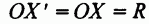и точка . Итак, а — плоскость симметрии сферы S

Симметричные тела встречаются повсюду: чайники, чашки, автомобили, дома, корабли, тела животных и т. д.

Вау!! 😲 Ты еще не читал? Это зря!

• шар ,
• сфера ,
• понятие симметрии , виды симметрии ,
• центральная симметрия параллелепипеда , симметрия параллелепипеда ,
• симметрии в призме , симметрии в пирамиде ,
• свойство симметрии относительно точки ,
• симметрия относительно прямой , ось симметрии ,
• симметрия относительно точки , центр симметрии ,
• Симметрии в физике
• Суперсимметрия
• Трансляционная симметрия
• Симметрии в биологии
• Асимметрия
• диссимметрии
• сферическая симметрия
• аксиальная симметрия
• радиальная симметрия
• трансляционная симметрия
• двусторонняя (билатеральная) симметрия
• Симметрия в химии
• Анизотропия
• Симметрия в религии и культуре

Я что-то не договорил про симметрия шара, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое симметрия шара, симметрия сферы, симметричность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия