Привет, сегодня поговорим про гомотетия в пространстве, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
гомотетия в пространстве , настоятельно рекомендую прочитать все из категории Стереометрия.
Теорема Преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость ( или в себя при k=1).
Доказательство Пусть, O – центр гомотетии и α - любая плоскость, не проходящая через точку O. Возьмем любую прямую AB в плоскости α. Преобразование гомотетии переводит точку A в точку A` на луче OA, а точку B в точку B` на луче OB, причем
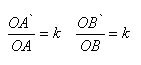
гомотетия в пространстве " />
где k – коэффициент гомотетии. Об этом говорит сайт https://intellect.icu . Отсюда следует подобие треугольников AOB и A`OB`. Из подобия треугольников следует равенство соответствующих углов AOB и A`OB, а значит, параллельность прямых AB и A`B`.
Возьмем теперь другую прямую AC в плоскости α. Она при гомотетии перейдет в параллельную прямую A`C`. При рассматриваемой гомотетии плоскость α перейдет в плоскость α`, проходящую через прямые A`B`, A`C`. Так как A`B` параллельна AB и A`C` параллельна AC, то по признаку параллельности плоскостей плоскости α и α` параллельны. Теорема доказана
Я что-то не договорил про гомотетия в пространстве, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое гомотетия в пространстве
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Стереометрия
Из статьи мы узнали кратко, но содержательно про гомотетия в пространстве
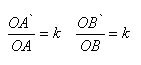 гомотетия в пространстве " />
гомотетия в пространстве " />
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия