Архимедовы тела кратко

Привет, Вы узнаете о том , что такое архимедовы тела, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое архимедовы тела , настоятельно рекомендую прочитать все из категории Стереометрия.

Существует семейство тел, родственных Платоновым - это полуправильные выпуклые многогранники, или архимедовы тела . У них все многогранные углы равны, все грани - правильные многоугольники, но нескольких различных типов. Существует 13 или 14 архимедовых тел (число неточное, поскольку псевдоромбокубоктаэдр иногда не причисляют к этому семейству): Усеченный икосаэдр, усеченный тетраэдр, усеченный куб, усеченный октаэдр, усеченный додекаэдр, ромбоусеченный кубоктаэдр, ромбоусеченный икосаэдр, ромбокубоктаэдр, ромбоикосододекаэдр, икосододекаэдр, кубоктаэдр, курносый куб, курносый додекаэдр, псевдоромбокубоктаэдр.

Открытие тринадцати полуправильных выпуклых многогранников приписывается Архимеду.

Архимедово тело (или архимедов многогранник) — выпуклый многогранник, имеющий в качестве граней два или более типов правильных многоугольников, примыкающих к идентичным вершинам. Здесь «идентичные вершины» означают, что для любых двух вершин существует изометрия всего тела, переводящая одну вершину в другую.

Архимедовы тела отличаются от платоновых тел (правильных многогранников), которые состоят только из одного типа многоугольников в одинаковых вершинах, и от многогранников Джонсона, правильные многоугольные грани которого принадлежат различным типам вершин.

Иногда только требуется, чтобы грани, прилегающие к одной вершине, были изометричными граням при другой вершине. Эта разница в определениях определяет, считается ли удлиненный квадратный гирокупол (псевдо­ромбо­кубо­октаэдр) архимедовым телом или многогранником Джонсона — это единственный выпуклый многогранник, в котором многоугольные грани примыкают к вершине одним и тем же способом в каждой вершине, но многогранник не имеет глобальную симметрию, которая бы переводила любую вершину в любую другую. Основываясь на существовании псевдо­ромбо­кубо­октаэдра, Грюнбаум предложил терминологическое различие, в котором архимедово тело определяется как имеющее одну и ту же вершинную фигуру в каждой вершине (включая удлиненный квадратный гирокупол), в то время как однородный многогранник определяется как тело, у которого любая вершина симметрична любой другой (что исключает гиробикупол).

Призмы и антипризмы, группами симметрий которых являются диэдрические группы, обычно не считаются архимедовыми телами, несмотря на то, что они подпадают под определение, данное выше. С этим ограничением существует только конечное число архимедовых тел. Все тела, кроме удлиненного квадратного гирокупола, можно получить построениями Витхоффа из платоновых тел с помощью тетраэдральной, октаэдральной[en] и икосаэдральной симметрий.

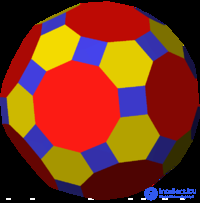
Ромбоусеченный икосо­додекаэдр является самым большим архимедовым телом по объему (для единичной длины ребра), а также имеющим больше всех других вершин и ребер.

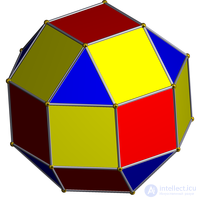
Псевдоромбокубооктаэдр имеет одну вершинную фигуру, 3.4.4.4, но с поворотом одного квадратного купола. В отличие от (не повернутого) ромбокубооктаэдра, фигура не является вершинно транзитивной.

Источник названия

Архимедовы тела названы по имени Архимеда, обсуждавшего их в ныне потерянной работе. Папп ссылается на эту работу и утверждает, что Архимед перечислил 13 многогранников . Во времена Возрождения художники и математики ценили чистые формы и переоткрыли их все. Эти исследования были почти полностью закончены около 1620 года Иоганном Кеплером , который определил понятия призм, антипризм и невыпуклых тел, известных как тела Кеплера — Пуансо.

Кеплер, возможно, нашел также удлиненный квадратный гиробикупол (псевдоромбоикосаэдр) — по меньшей мере, он утверждал, что имеется 14 архимедовых тел. Однако его опубликованные перечисления включают только 13 однородных многогранников, и первое ясное утверждение о существовании псевдоромбоикосаэдра было сделано в 1905 Дунканом Соммервилем[en] .

Классификация

Существует 13 архимедовых тел (не считая удлиненного квадратного гирокупола; 15, если учитывать зеркальные отражения двух энантиоморфов, которые ниже перечислены отдельно).

Здесь вершинная конфигурация относится к типам правильных многоугольников, которые примыкают к вершине. Например, вершинная конфигурация (4,6,8) означает, что квадрат, шестиугольник и восьмиугольник встречаются в вершине (порядок перечисления берется по часовой стрелке относительно вершины).

Название (Альтернативное название)	Шлефли Коксетер	Прозрачный	Непрозрачный	Развертка	Вершинная фигура	Граней		Ребер	Вершин	Объем (при единич- ном ребре)	Группа точек
Усеченный тетраэдр	{3,3}				3.6.6	8	4 треугольника 4 шестиугольника	18	12	2.710576	Td
Кубооктаэдр (ромботетраэдр)	r{4,3} или rr{3,3} или				3.4.3.4	14	8 Треугольников 6 квадратов	24	12	2.357023	Oh
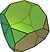
Усеченный куб	t{4,3}				3.8.8	14	8 треугольников 6 восьмиугольников	36	24	13.599663	Oh
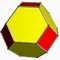
Усеченный октаэдр (усеченный тетратераэдр)	t{3,4} или tr{3,3} или				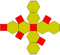4.6.6	14	6 квадратов 8 шестиугольников	36	24	11.313709	Oh
Ромбокубооктаэдр (малый ромбокубооктаэдр)	rr{4,3}				3.4.4.4	26	8 треугольников 18 квадратов	48	24	8.714045	Oh
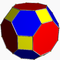
Усеченный кубооктаэдр (большой ромбокубооктаэдр)	tr{4,3}				4.6.8	26	12 квадратов 8 шестиугольников 6 восьмиугольников	72	48	41.798990	Oh
Плосконосый куб (плосконосый кубоктаэдр)	sr{4,3}				3.3.3.3.4	38	32 треугольника 6 квадратов	60	24	7.889295	O
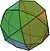
Икосододекаэдр	r{5,3}				3.5.3.5	32	20 треугольников 12 пятиугольников	60	30	13.835526	Ih
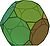
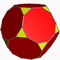
Усеченный додекаэдр	t{5,3}				3.10.10	32	20 треугольников 12 десятиугольников	90	60	85.039665	Ih
Усеченный икосаэдр	t{3,5}				5.6.6	32	12 пятиугольников 20 шестиугольников	90	60	55.287731	Ih
Ромбоикосододекаэдр (малый ромбоикосододекаэдр)	rr{5,3}				3.4.5.4	62	20 треугольников 30 квадратов 12 пятиугольников	120	60	41.615324	Ih
Ромбоусеченный икосододекаэдр	tr{5,3}				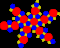4.6.10	62	30 квадратов 20 шестиугольников 12 десятиугольников	180	120	206.803399	Ih
Плосконосый додекаэдр (плосконосый икосододекаэдр)	sr{5,3}				3.3.3.3.5	92	80 треугольников 12 пятиугольников	150	60	37.616650	I

Некоторые определения полуправильных многогранников включают еще одно тело — удлиненный квадратный гирокупол или «псевдоромбокубооктаэдр» .

Свойства

Число вершин равно отношению 720° к угловому дефекту при вершине.

Кубоктаэдр и икосододекаэдр являются реберно однородными[en] и называются квазиправильными.

Двойственные многогранники архимедовых тел называются каталановыми телами. Об этом говорит сайт https://intellect.icu . Вместе с бипирамидами и трапецоэдрами они являются однородными по граням телами с правильными вершинами.

Хиральность

Плосконосый куб и плосконосый додекаэдр хиральны, поскольку они появляются в левостороннем и правостороннем вариантах. Если что-то имеет несколько видов, которые являются трехмерным зеркальным отражением друг друга, эти формы называют энантиоморфами (это название применяется также для некоторых форм химических соединений).

Построение архимедовых тел

Подробное рассмотрение темы: Однородные многогранники и Нотация многогранников Конвея

Архимедовы тела могут быть построены с помощью положения генератора в калейдоскопе

Различные архимедовы и платоновы тела могут быть получены друг из друга с помощью пригоршни операций. Начиная с платоновых тел можно использовать операцию усечения углов. Для сохранения симметрии усечение делается плоскостью, перпендикулярной прямой, соединяющей угол с центром многоугольника. В зависимости от того, насколько глубоко проводится усечение (см. таблицу ниже), получим различные платоновы и архимедовы (и другие) тела. Растяжение или скашивание осуществляется путем движения граней (в направлении) от центра (на одно и то же расстояние, чтобы сохранить симметрию) и созданием, затем, выпуклой оболочки. Расширение с поворотом осуществляется также вращением граней, это ломает прямоугольники, возникающие на местах ребер, на треугольники. Последнее построение, которое мы здесь приводим, это усечение как углов, так и ребер. Если игнорировать масштабирование, расширение можно также рассматривать как усечение углов и ребер, но с определенным отношением между усечениями углов и ребер.

Построение архимедовых тел

Симметрия		Тетраэдральная	Октаэдральная[en]		Икосаэдральная
Начальное тело Операция	Символ {p, q}	Тетраэдр {3,3}	Куб {4,3}	Октаэдр {3,4}	Додекаэдр {5,3}	Икосаэдр {3,5}
Усечение (t)	t{p, q}	Усеченный тетраэдр	Усеченный куб	Усеченный октаэдр	Усеченный додекаэдр	Усеченный икосаэдр
Полное усечение (r) Амвон (a)	r{p, q}	Тетратетраэдр	Кубооктаэдр		Икосододекаэдр
Глубокое усечение[en] (2t) (dk)	2t{p, q}	Усеченный тетраэдр	усеченный октаэдр	усеченный куб	усеченный икосаэдр	усеченный додекаэдр
Двойное полное усечение (2r) Двойственный (d)	2r{p, q}	тетраэдр	октаэдр	куб	икосаэдр	додекаэдр
Скашивание (rr) Растяжение (e)	rr{p, q}	Кубооктаэдр	Ромбокубооктаэдр		ромбоикосододекаэдр
Плосконосое спрямление (sr) Спрямление (s)	sr{p, q}	плосконосый тетратетраэдр	плосконосый куб		плосконосый икосододекаэдр
скос-усечение[en] (tr) Скашивание (b)	tr{p, q}	Усеченный октаэдр	Усеченный кубооктаэдр		Ромбоусеченный икосододекаэдр

Заметим двойственность между кубом и октаэдром и между додекаэдром и икосаэдром. Также, частично вследствие самодвойственности тетраэдра, только одно архимедово тело имеет только одну тетраэдральную симметрию.

Вау!! 😲 Ты еще не читал? Это зря!

• Апериодическая мозаика
• Архимедов граф
• Список однородных многогранников
• Тороидальный многогранник
• Квазикристалл
• Полуправильный многогранник
• Правильный многогранник
• Однородный многогранник
• Икосоэдральный двойник
• центральная симметрия параллелепипеда , симметрия параллелепипеда , симметрия куба , осевая симметрия параллелепипеда ,

Исследование, описанное в статье про архимедовы тела, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое архимедовы тела и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия