Звездчатые Тела Кеплера - Пуансона кратко

Привет, Вы узнаете о том , что такое тела кеплера - пуансона , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое тела кеплера - пуансона , настоятельно рекомендую прочитать все из категории Стереометрия.

Тело Кеплера — Пуансо — тело, представляющее собой правильный звездчатый многогранник, не являющийся соединением платоновых и звездчатых тел.

Если же продлить все грани октаэдра до пересечения их друг с другом, то получится фигура, которую Иоганн Кеплер назвал - "стелла октангула" (продолженным октаэдром). Она встречается и в природе: это так называемый двойной кристалл. Мы вынуждены признать «стеллу октангулу» правильным многогранником: ведь все ее грани - правильные треугольники одинакового размера и все углы между ними равны!

В 1811 году французский математик Огюстен Коши установил, что существуют всего 4 правильных звездчатых тела, которые не являются соединениями платоновых и звездчатых тел . К ним относятся открытые в 1619 году Иоганном Кеплером малый звездчатый додекаэдр и большой звездчатый додекаэдр, а также большой додекаэдр и большой икосаэдр, открытые в 1809 году Луи Пуансо . Остальные правильные звездчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кеплера — Пуансо

«стелла октангула»

Что же это - шестое Платоново тело?! Нет, так как эти многогранник не является выпуклым.

Кроме «продолженного октаэдра», необходимо добавить еще четыре многогранника, каждый из которых будет «почти правильным». Все они получаются «озвездыванием» Платонова тела, то есть продлением его граней до пересечения друг с другом, и потому называются звездчатыми. Куб и тетраэдр не порождают новых фигур - грани их, сколько ни продолжай, не пересекаются.

Икосаэдр и додекаэдр дарят миру сразу четыре «почти правильных многогранника». Один из них - малый звездчатый додекаэдр, полученный впервые Иоганном Кеплером.

Малый звездчатый додекаэдр

Большой звездчатый додекаэдр

Кеплер не додумался, что у полученной им фигуры есть двойник. Многогранник, который называется «большой додекаэдр» - построил французский геометр Луи Пуансон спустя двести лет после кеплеровских звездчатых фигур.

Звездчатый икосаэдр

Большой икосаэдр был впервые описан Луи Пуансон в 1809 году. И опять Кеплер, "увидев" большой звездчатый додекаэдр, честь открытия второй фигуры оставил Луи Пуансону.

Большой икосаэдр

Эти фигуры "наполовину" подчиняются формуле Эйлера.

История

Мозаика в соборе Святого Марка в Венеции, иногда приписывается Паоло Уччелло.

Некоторые из многогранников Кеплера — Пуансо в той или иной форме были известны еще до Кеплера . Так, изображение малого звездчатого додекаэдра присутствует в мраморной мозаике, украшающей пол собора Святого Марка в Венеции. Эта мозаика датируется XV веком, авторство иногда приписывается Паоло Уччелло. В XVI веке немецкий ювелир Венцель Ямнитцер (англ.)русск. в своем труде Perspectiva corporum regularium (рус. Перспективы правильных тел) изображает большой додекаэдр и большой звездчатый додекаэдр . По-видимому, до Кеплера никто из художников и ученых не знал всех свойств этих тел.

Малый и большой звездчатые додекаэдры, которые иногда именуют «многогранники Кеплера», впервые были полностью описаны в трактате Иоганна Кеплера 1619 года Harmonices Mundi . Каждое из этих тел имеет центральную выпуклую область каждой грани, «скрытую» внутри, при этом видны только треугольные плоскости. Кеплер описывает многогранники, используя ту же модель, с помощью которой Платон в диалоге Тимей описывает построение правильных многогранников на основе правильных треугольников . Последним шагом Кеплера было признание, что эти многогранники являются правильными, даже если они не являются выпуклыми, в отличие от обычных платоновых тел.

В 1809 году Луи Пуансо вновь исследовал многогранники Кеплера и обнаружил еще два правильных звездчатых многогранника — большой икосаэдр и большой додекаэдр . При этом Пуансо не был уверен, что выявил все возможные виды правильных звездчатых многогранников. Но в 1811 году Огюстен Луи Коши доказал, что существуют всего 4 правильных звездчатых тела, которые не являются соединениями платоновых и звездчатых тел, а в 1858 году, Жозеф Бертран представил более общее доказательство . В 1859 году Артур Кэли дал многогранникам Кеплера — Пуансо названия, под которыми они, как правило, известны сегодня . Сто лет спустя Джон Конвей разработал терминологию для звездчатых многоугольников. Об этом говорит сайт https://intellect.icu . В рамках этой терминологии он предложил слегка измененные имена для двух из правильных звездчатых многогранников .

Терминология Кэли	Терминология Конвея
Малый звездчатый додекаэдр	Звездчатый додекаэдр
Большой додекаэдр	Большой додекаэдр
Большой звездчатый додекаэдр	Звездчатый большой додекаэдр
Большой икосаэдр	Большой икосаэдр

Терминология Конвея в настоящее время используется, но не имеет широкого распространения.

Характеристики

Невыпуклость

Эти тела имеют плоскости в виде пятиугольников. Малый и большой звездчатый додекаэдры имеют плоскости в виде невыпуклых правильных звезд. Большой додекаэдр и большой икосаэдр имеют выпуклые плоскости [10].

У всех этих тел две плоскости могут пересекаться, образуя линию, которая не является ребром какой-либо плоскости, и, таким образом, часть каждой грани проходит через внутреннюю часть тела. Такие линии пересечения иногда называются ложными ребрами. Аналогично, в случае, когда три таких линии пересекаются в точке, не принадлежащей углу какой-либо плоскости, эти точки называются ложными вершинами. Например, малый звездчатый додекаэдр имеет 12 пятиугольных граней с центральной пятиугольной частью, скрытой внутри тела. Видимые части каждой грани состоят из пяти равнобедренных треугольников, которые касаются грани в пяти точках. Можно рассмотреть эти треугольники как 60 отдельных плоскостей, образующих новый, неправильный многогранник, который внешне выглядит идентичным изначальному. Каждое ребро теперь будет разделено на три коротких ребра (двух разных видов), при этом 20 ложных вершин станут истинными, и, таким образом, в общей сложности у тела будет 32 вершины (опять-таки двух видов). Скрытые внутренние пятиугольники больше не будут являться часть многогранной поверхности, и могут исчезнуть. Теперь Эйлерова характеристика содержит: 60 — 90 + 32 = 2. Но этот новый многогранник уже не описывается символом Шлефли {5/2, 5} , и поэтому не является телом Кеплера — Пуансо, хотя по-прежнему выглядит, как одно из них[10].

Эйлерова характеристика χ

Тела Кеплера — Пуансо покрывают площадь описанных вокруг них сфер более одного раза, при этом центры граней выступают в качестве точек перегиба на поверхностях, имеющих пятиугольные плоскости, и вершин — на других поверхностях. Из-за этого тела Кеплера — Пуансо не обязательно топологически эквивалентны сфере, в отличие от платоновых тел, и, в частности, Эйлерова характеристика

для них не всегда имеет место. Шлефли установил, что все многогранники должны иметь χ = 2, и счел, что малый звездчатый додекаэдр и большой додекаэдр не являются правильными многогранниками[11]. Эта точка зрения не была широко распространенной.

Модифицированная форма формулы Эйлера, выведенная Артуром Кэли , справедливая как для выпуклых многогранников, так и для тел Кеплера — Пуансо, выглядит так:

.

Electron in the transistor-resistor kingdom

Game: Perform tasks and rest cool.2 people play!

Play game

Двойственность

Тела Кеплера — Пуансо существуют в двойственных (дуальных) парах[12]:

• Малый звездчатый додекаэдр — большой додекаэдр
• Большой звездчатый додекаэдр — большой икосаэдр.

Сводная таблица свойств

Свойства тел Кеплера-Пуансо представлены в следующей таблице:

Название	Малый звездчатый додекаэдр	Большой додекаэдр	Большой звездчатый додекаэдр	Большой икосаэдр
Изображение
Сферическая проекция
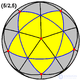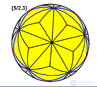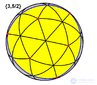Диаграмма звездчатого многогранника
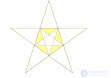Символ Шлефли {p, q}	{5/2,5}	{5,5/2}	{5/2,3}	{3,5/2}
Поверхности {p}	12 {5/2}	12 {5}	12 {5/2}	20 {3}
Ребра	30	30	30	30
Вершины	12 {5}	12 {5/2}	20 {3}	12 {5/2}
χ Эйлерова характеристика	-6	-6	2	2
Плотность	3	3	7	7
Группы симметрии	Ih	Ih	Ih	Ih
Двойственный многогранник	Большой додекаэдр	Малый звездчатый додекаэдр	Большой икосаэдр	Большой звездчатый додекаэдр

Отношения между правильными многогранниками

Имеют одно и то же расположение вершин:	Имеют одни и те же вершины и ребра:
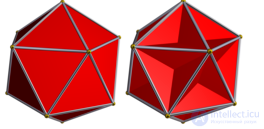
Икосаэдр, Малый звездчатый додекаэдр, Большой икосаэдр и Большой додекаэдр.	Малый звездчатый додекаэдр и Большой икосаэдр.
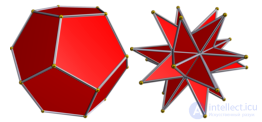Додекаэдр и Большой звездчатый додекаэдр.	Икосаэдр и Большой додекаэдр.

Малый звездчатый додекаэдр и большой икосаэдр имеют одни и те же вершины и ребра. Икосаэдр и большой додекаэдр также имеют одни и те же вершины и ребра.

Все три додекаэдра являются звездчатыми правильными выпуклыми додекаэдрами, большой икосаэдр является звездчатым правильным выпуклым икосаэдром[14].

Если при пересечении фигур возникают новые ребра и вершины, полученные многогранники не будут правильными, но их еще можно считать звездчатыми.

В массовой культуре и искусстве

Звезда Александера

В XX веке известный представитель имп-арта Мауриц Эшер в своем творчестве нередко обращался к сюжетам, основанным на восприятии различных многомерных фигур; в частности, его литография Гравитация (англ.)русск. изображает малый звездчатый додекаэдр .

В основу перестановочной головоломки 1980-х годов — звезды Александера — положен большой додекаэдр .

Вау!! 😲 Ты еще не читал? Это зря!

• Правильные многомерные многогранники
• Однородный звездчатый многогранник
• центральная симметрия параллелепипеда , симметрия параллелепипеда , симметрия куба , осевая симметрия параллелепипеда ,

Исследование, описанное в статье про тела кеплера - пуансона , подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое тела кеплера - пуансона и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия