Симметрия относительно плоскости. Плоскость симметрии кратко

Привет, Вы узнаете о том , что такое симметрия относительно плоскости, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое симметрия относительно плоскости, плоскость симметрии , настоятельно рекомендую прочитать все из категории Стереометрия.

4.1.Определение симметрии относительно плоскости

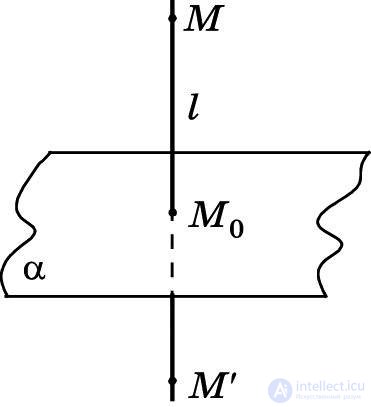
Рис. 19

ОПРЕДЕЛЕНИЕ. Точка m′ пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ′ перпендикулярен этой плоскости и делится ею пополам. Любая точка плоскости α считается симметричной самой себе относительно этой плоскости (рис. 19).

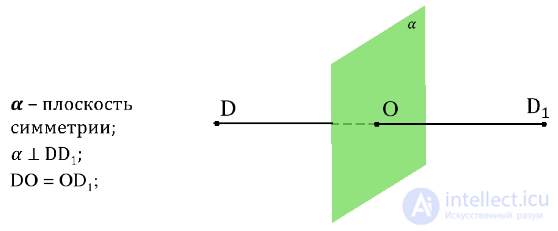
Из определения следует, что если точка M′ симметрична точке M относительно плоскости α, то точка М симметрична точке М′ относительно той же плоскости α.

Зададим теперь следующее отображение пространства на себя. Каждой точке М пространства поставим в соответствие точку М′, симметричную ей относительно плоскости α. Аналогично центральной симметрии, можно доказать, что это отображение является преобразованием пространства. При этом каждая точка плоскости α отображается на себя.

симметрия относительно плоскости означает, что фигура или объект выглядит одинаково, если его отразить относительно данной плоскости. плоскость симметрии является осью, вокруг которой происходит отражение, и разделяет фигуру на две равные половины, которые являются зеркальными отражениями друг друга.

Например, если мы возьмем простой пример буквы "А" и проведем плоскость симметрии вертикально посередине буквы, то обе ее половины будут идентичными зеркальными отражениями друг друга. То есть, отражение одной половины буквы "А" относительно плоскости симметрии приведет к получению полностью идентичной другой половины.

Симметрия относительно плоскости имеет широкое применение в геометрии и искусстве. Множество объектов и фигур, таких как окружности, квадраты, треугольники, растения, животные и т.д., могут обладать симметрией относительно различных плоскостей. Этот тип симметрии визуально приятен и часто используется для создания эстетически привлекательных композиций и дизайнов.

ОПРЕДЕЛЕНИЕ. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется симметрией пространства относительно плоскости α. Плоскость α называется плоскостью симметрии.

Симметрия относительно плоскости α обозначается Sα. Если при этой симметрии точка М (фигура F) отображается на точку М′ (фигуру F′), то записывают Sα(М) = М′ (Sα(F) = F′). Это преобразование еще называют «отражением в плоскости», или «зеркальной симметрией», или «зеркальным отражением от плоскости», проводя аналогию с «отражением в зеркале».

Из определения симметричных точек относительно плоскости α следует

Sα(M) = M′ ⇔ Sα(M′) = M.

Поэтому говорят, что точки М и М′ симметричны относительно плоскости α. С другой стороны, ранее было показано, что точка M′ отображается на свой прообраз — точку M — преобразованием, обратным данному. Значит,

Sα(M) = M′ ⇒ 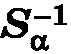(M′) = M.

Получили

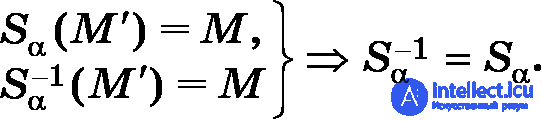
Таким образом, симметрия относительно плоскости есть преобразование пространства, совпадающее со своим обратным преобразованием.

Тогда для любой точки М пространства имеем

(Sα ∘ Sα)(M) = Sα(Sα (M)) = Sα(M′) = 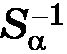(M′) = M.

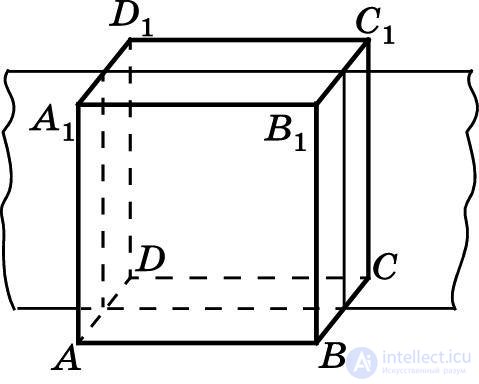
Рис. Об этом говорит сайт https://intellect.icu . 20

Но для тождественного преобразования E справедливо Е(М) = М. Так как точка М — любая, то преобразования Sα ∘ Sα и Е равны: Sα ∘ Sα = Е, т. е. композиция двух симметрий относительно одной и той же плоскости есть тождественное преобразование.

Если при симметрии относительно плоскости α фигура F отображается на себя (Sα(F) = F), то плоскость α называется плоскостью симметрии этой фигуры. При этом говорят, что фигура F симметрична относительно плоскости α (или плоскость α является плоскостью симметрии фигуры F).

Например, плоскость, проходящая через середины параллельных ребер AD, ВС, B1C1 и A1D1 куба АВСDA1B1C1D1 (рис. 20), является плоскостью симметрии этого куба. Докажите это и найдите другие плоскости симметрии данного куба.

Симметрия относительно плоскости может быть задана парой соответственных (симметричных) точек А и A′ (почему?).

4.2.Симметрия относительно плоскости в координатной форме

Выведем формулы, которые позволяли бы по координатам произвольной точки М пространства находить координаты ее образа — точки M′ = Sα(M).

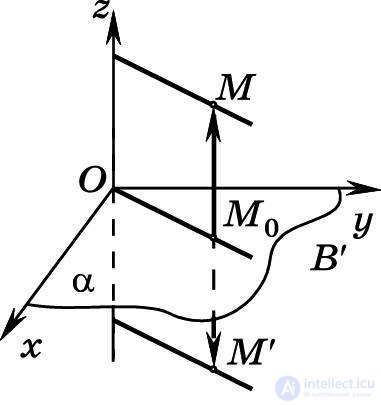
Рис. 21

Выберем прямоугольную систему координат Oхyz так, чтобы ее координатная плоскость Оху совпадала с плоскостью симметрии α. Рассмотрим в этой системе координат произвольную точку M(x; y; z) и ее образ М′(x′; y′; z′) при симметрии относительно плоскости Oxy (рис. 21).

По определению симметрии относительно плоскости имеем MM′ ⟂ (Оху), | M0M | = | M0M′ |, где M0 — точка пересечения прямой ММ′ с плоскостью Оху. Это означает, что точки М и M′ расположены в разных полупространствах относительно плоскости Oxy, одинаково удалены от нее, а прямая MM′ параллельна координатной оси Oz. Поэтому координаты этих точек связаны соотношениями

x′ = x, y′ = y, z′ = –z,

которые называются формулами npeoбразованuя симметрии относительно плоскости Oxy.

4.3.Симметрия относительно плоскости — движение пространства

Используя формулы симметрии в координатах, докажем, что симметрия относительно плоскости — движение пространства.

Пусть A(x1; y1; z1), C(x2; y2; z2) — данные точки, тогда A′(x1; y1; –z1), C′(x2; y2; –z2) — их образы при симметрии S(Oxy).

Находим:

| АC | = ;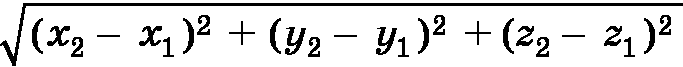
| A′C′ | = =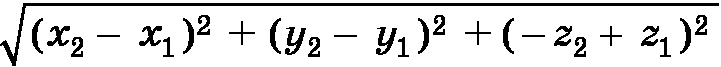
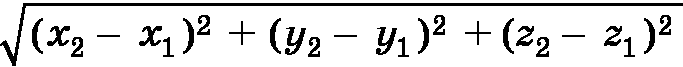= = | AC |,

т. е. рассматриваемая симметрия является движением, что и требовалось доказать. ▼

4.4. Свойства симметрии относительно плоскости

Рассмотрим вопрос о неподвижных точках, неподвижных прямых и неподвижных плоскостях зеркальной симметрии.

Неподвижной точкой симметрии относительно плоскости α является каждая точка плоскости α; других неподвижных точек при данной симметрии нет.

Неподвижные прямые симметрии Sα относительно плоскости α можно разделить на два вида:

—каждая прямая плоскости α; любая точка такой прямой является неподвижной точкой симметрии Sα, а симметрия Sα индуцирует на каждой из этих прямых тождественное преобразование Е;

—каждая прямая пространства, перпендикулярная плоскости α; на любой такой прямой индуцируется центральная симметрия относительно точки пересечения этой прямой с плоскостью α.

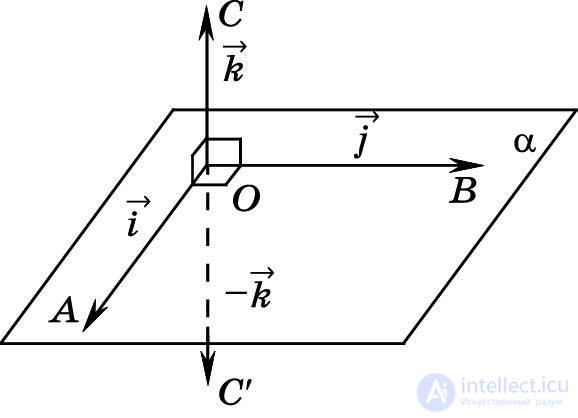
Рис. 22

Неподвижные плоскости симметрии Sα можно разделить также на два вида:

—сама плоскость α; каждая ее точка является неподвижной точкой симметрии Sα, а симметрия Sα индуцирует на этой плоскости тождественное преобразование E;

—каждая плоскость, перпендикулярная плоскости α; на любой такой плоскости индуцируется известная вам из планиметрии осевая симметрия относительнo прямой пересечения этой плоскости с плоскостью α.

Для исследования вопроса о том, меняет ли симметрия относительно плоскости ориентацию тетраэдра, выберем такую тройку единичных попарно взаимно перпендикулярных векторов 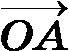, 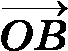и , чтобы точки O, А и В лежали в плоскости α. Тогда при симметрии Sα тетраэдр ОАВС отобразится на такой тетраэдр ОАВC′, что ′ = – (рис. 22). Это означает, что ориентации тетраэдров ОАВС и ОАВC′ = Sα(OABC) различны, т. е. симметрия относительно плоскости меняет ориентацию тетраэдра, следовательно, является движением второго рода.

Интересно заметить, что если три плоскости α, β и γ попарно взаимно перпендикулярны, то композиция симметрий относительно этих трех плоскостей является центральной симметрией относительно их общей точки (точки пересечения плоскостей α, β и γ), т. е. Sγ ∘ Sβ ∘ Sα = ZО, где О — общая точка этих трех плоскостей. Попробуйте самостоятельно доказать это координатным методом.

Плоскость симметрии - это гипотетическая плоскость, которая делит объект на две равные и зеркально отраженные части. Когда объект отражается относительно этой плоскости, он остается неизменным или симметричным.

Плоскость симметрии может быть вертикальной, горизонтальной или диагональной, в зависимости от ориентации объекта. Например, у прямоугольника плоскость симметрии может быть горизонтальной, проходящей по его центру, таким образом, верхняя половина будет зеркальным отражением нижней половины.

У некоторых объектов может быть несколько плоскостей симметрии. Например, у равностороннего треугольника есть три плоскости симметрии - каждая из сторон треугольника является плоскостью симметрии, делит треугольник на две равные части.

Плоскость симметрии играет важную роль в геометрии, искусстве и других областях. Она помогает в создании сбалансированных и гармоничных композиций, а также используется в определении свойств объектов и фигур.

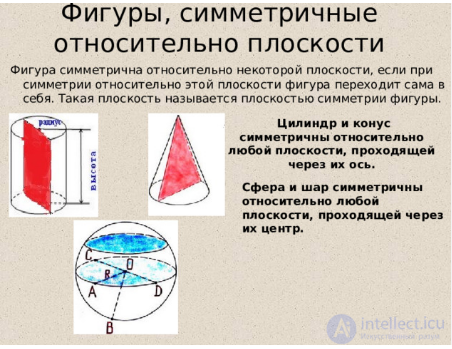
Фигуры симметричные относительно плоскости

Вау!! 😲 Ты еще не читал? Это зря!

• понятие симметрии , виды симметрии ,
• симметрия шара , симметрия сферы ,
• центральная симметрия параллелепипеда , симметрия параллелепипеда ,
• симметрии в призме , симметрии в пирамиде ,
• свойство симметрии относительно точки ,
• симметрия относительно прямой , ось симметрии ,
• симметрия относительно точки , центр симметрии ,
• Симметрии в физике
• Суперсимметрия
• Трансляционная симметрия
• Симметрии в биологии
• Асимметрия
• диссимметрии
• сферическая симметрия
• аксиальная симметрия
• радиальная симметрия
• трансляционная симметрия
• двусторонняя (билатеральная) симметрия
• Симметрия в химии
• Анизотропия
• Симметрия в религии и культуре

Исследование, описанное в статье про симметрия относительно плоскости, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое симметрия относительно плоскости, плоскость симметрии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия