Симметрии в призме и в пирамиде кратко

Привет, Вы узнаете о том , что такое симметрии в призме, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое симметрии в призме, симметрии в пирамиде , настоятельно рекомендую прочитать все из категории Стереометрия.

Симметрия прямой призмы

Плоскость симметрии, проходящая через середины боковых ребер .

Симметрия правильной призмы

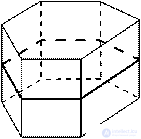
1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы

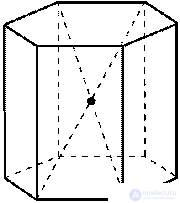
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра

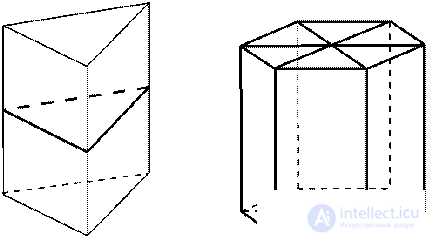
3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней .

Симметрия правильной призмы

Напомним, что правильной называется прямая призма, в основании которой лежит правильный многоугольник. Симметричность правильных призм определяется симметричностью их оснований (рис. 1), а так же перпендикулярностью основаниям боковых ребер и граней.

У правильной n-угольной призмы имеется n плоскостей симметрии, проходящих через соответствующие оси симметрии оснований призмы (рис. 2).

Кроме того, у нее имеется еще одна плоскость симметрии, которая проходит через середины боковых ребер (рис. 7/15).

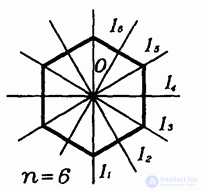
рис. Об этом говорит сайт https://intellect.icu . 1

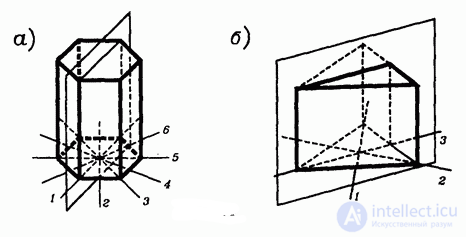
рис. 2

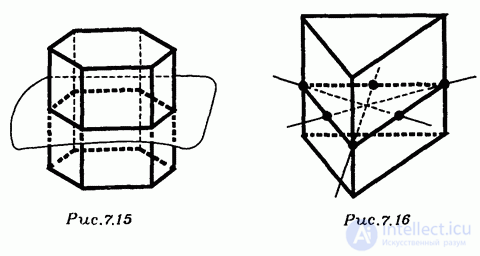
Осями симметрии правильной n -угольной призмы всегда являются n осей симметрии сечения этой призмы, проходящего через середины боковых ребер (рис. 7.16). Если к тому же четно, то n осью симметрии является еще прямая, которая соединяет центры оснований (рис. 7.17). Если же нечетно, то это не так и других n осей симметрии нет.

Отрезок, соединяющий центры оснований правильной призмы, называется ее осью (рис. 7.17).

Если n - четно, то середина оси правильной -угольной призмы является центром симметрии этой призмы (рис. 7.18).

Если же n - нечетно, то центра симметрии у правильной призмы нет (как и у ее основания).

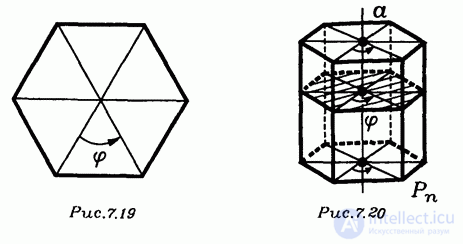
Итак, симметричность правильной n-угольной призмы определяется симметричностью ее основания — правильного n-угольника. Но, как известно из планиметрии, правильные n-угольники имеют еще один вид симметрии — вращательную, т. е. они самосовмещаются при повороте вокруг своего центра на угол 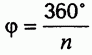(рис. 7.19), а также на любой угол, кратный . Аналогично, правильные n -угольные призмы самосовмещаются при повороте вокруг своей оси на такой же угол (рис. 7.20).

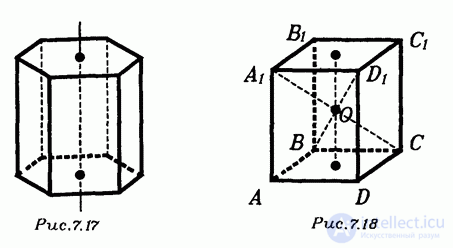
Подробнее это означает следующее. Плоскости, перпендикулярные оси правильной n -угольной призмы Р, параллельны ее основанию. Поэтому все сечения призмы Р такими плоскостями равны ее основанию и проектируются на него. Центры этих правильных n -угольников лежат на оси призмы. Поэтому, если эти многоугольники одновременно повернуть в их плоскостях в одном направлении на угол 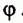вокруг их центров, то все они самосовместятся. А потому при таком преобразовании и призма Р самосовместится. Такое преобразование призмы называется поворотом вокруг прямой — оси призмы — на угол 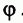Тем самым призма среди симметрий имеет и поворотную симметрию.

Заметим еще, что осевая симметрия в пространстве является поворотом на 180° вокруг оси симметрии. Действительно, в результате поворота на 180° вокруг

прямой а точка X, не лежащая на прямой а, перейдет в такую точку X`, что прямая а перпендикулярна отрезку XX` и пересекает его в середине.

Симметрия правильной пирамиды

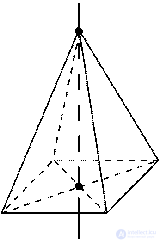
1. Плоскости симметрии: при четном числе сторон основания — плоскости, проходящие через противолежащие боковые ребра; и плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней (рис. 15).

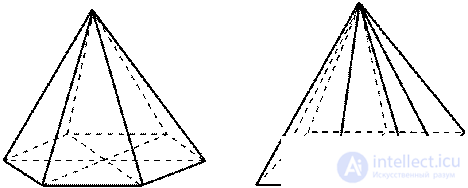
2. Ось симметрии: при четном числе сторон основания — ось симметрии, проходящая через вершину правильной пирамиды и центр основания .

Вау!! 😲 Ты еще не читал? Это зря!

• понятие симметрии , виды симметрии ,
• симметрия шара , симметрия сферы ,
• центральная симметрия параллелепипеда , симметрия параллелепипеда ,
• свойство симметрии относительно точки ,
• симметрия относительно прямой , ось симметрии ,
• симметрия относительно точки , центр симметрии ,
• Симметрии в физике
• Суперсимметрия
• Трансляционная симметрия
• Симметрии в биологии
• Асимметрия
• диссимметрии
• сферическая симметрия
• аксиальная симметрия
• радиальная симметрия
• трансляционная симметрия
• двусторонняя (билатеральная) симметрия
• Симметрия в химии
• Анизотропия
• Симметрия в религии и культуре

Исследование, описанное в статье про симметрии в призме, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое симметрии в призме, симметрии в пирамиде и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия