Лекция
Привет, сегодня поговорим про центральная симметрия параллелепипеда, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое центральная симметрия параллелепипеда, симметрия параллелепипеда, симметрия куба, осевая симметрия параллелепипеда, симметрия многогранников , настоятельно рекомендую прочитать все из категории Стереометрия.
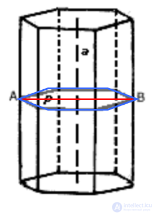
Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Поэтому противоположные вершины параллелепипеда симметричны относительно этой точки. Следовательно, каждый параллелепипед имеет центр симметрии — точку пересечения его диагоналей (рис 1.).
В общем случае осей и плоскостей симметрии параллелепипед не имеет, Прямой, но не прямоугольный параллелепипед всегда имеет ось симметрии — прямую, проходящую через центры симметрии его оснований, и плоскость симметрии, проходящую через середины его боковых ребер.
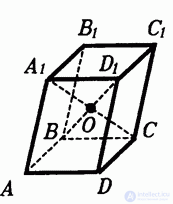
Рисунок 1
Если основания прямого параллелепипеда — ромбы (но не квадраты), то появляются еще две оси и две плоскости симметрии (Рис 2).
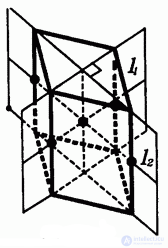
Рисунок 2
Найдите сами элементы симметрии прямоугольного параллелепипеда, среди граней которого нет квадратов.
Если среди граней прямоугольного параллелепипеда есть квадраты, то он является правильной четырехугольной призмой.
Центр симметрии прямоугольного параллелепипеда — точка пересечения диагоналей
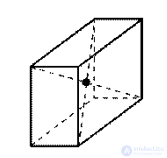
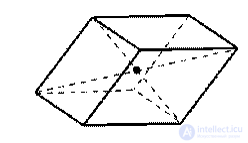
Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер.
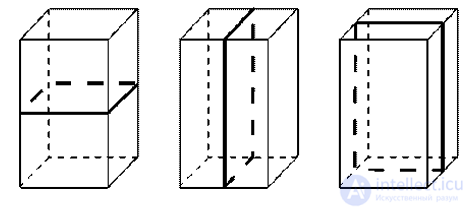
Оси симметрии: три оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней.
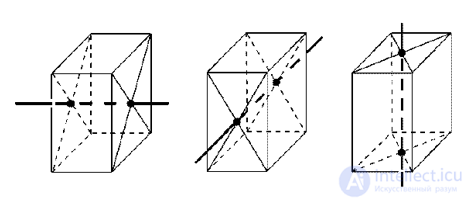
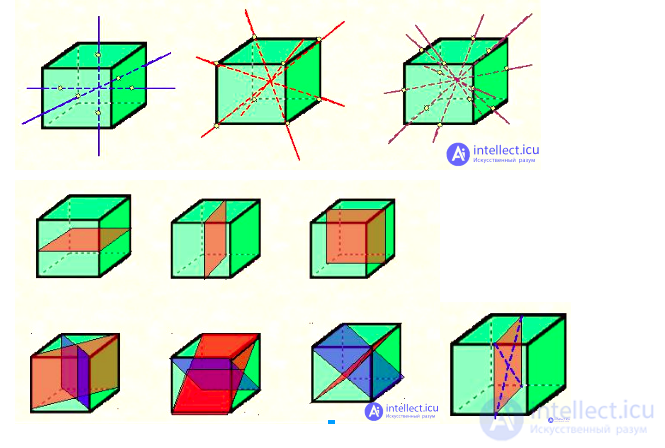
Куб имеет один центр симметрии – точку пересечения его диагоналей. Прямые а и b, проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Куб имеет девять осей симметрии. Обратите внимание, все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии.

Три плоскости симметрии, проходящие через середины параллельных ребер и шесть плоскостей симметрии , проходящие через противолежащие ребра.
Теорема
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Доказательство
Рассмотрим любые две диагонали параллелепипеда, например A1A3` и A4A2`. Так как четырехугольники A1A2A3A4 и A2A2`A3`A3 – параллелограммы с общей стороной A2A3, то их стороны A1A4 и A2`A3` параллельны друг другу, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскости противолежащих граней параллелепипеда по параллельным прямым A1A2` и A4A3`. Следовательно, четырехугольник A4A1A2`A3` - параллелограмм. Диагонали параллелепипеда A1A3` и A2A4` являются диагоналями этого параллелограмма. Поэтому они пересекаются и точкой пересечения O делятся пополам.
Аналогично доказывается, что диагонали A1A3` и A2A4`, а также диагонали A1A3` и A3A1` пересекаются и точкой пересечения делятся пополам. Об этом говорит сайт https://intellect.icu . Теорема доказана.
Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают. Под симметрией (или преобразованием симметрии) многогранника мы понимаем такое его движение в пространстве (например, поворот вокруг некоторой прямой, отражение относительно некоторой плоскости и т.д.), которое оставляет неизменными множества вершин, ребер и граней многогранника.
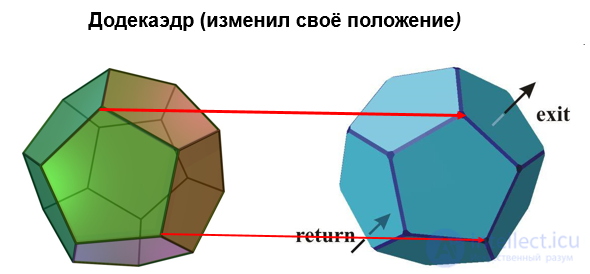
Рисунок Движение додекаэдра
Иначе говоря, под преобразованием симметрии вершина, ребро или грань либо сохраняет свое исходное положение, либо переводится в исходное положение другой вершины, другого ребра или другой грани. Существует одна симметрия, которая свойственна всем многогранникам. Речь идет о тождественном преобразовании, оставляющем любую точку в исходном положении.
С самым распространенным примером симметрии мы встречаемся в случае прямой правильной n-угольной призмы. Пусть a – прямая, соединяющая центры оснований. Поворот вокруг a на любое целое кратное угла 360/n градусов является симметрией. Пусть, далее, p – плоскость, проходящая посредине между основаниями параллельно им.
Отражение относительно плоскости p(движение, переводящее любую точку A в точку B, такую, что p пересекает отрезок AB под прямым углом и делит его пополам) – еще одна симметрия.
Риунок 10
Таблица 1 - Элементы симметрии правильных многогранников
|
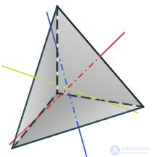
Тетраэдр
|
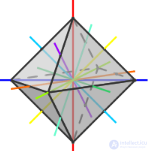
Октаэдр
|
Икосаэдр
|
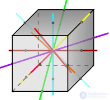
Гексаэдр (куб)
|
Додекаэдр
|
|
| Количество граней | 4 | 8 | 20 | 6 | 12 |
| количество ребер | 6 | 12 | 30 | 12 | 30 |
| вершин | 4 | 6 | 12 | 8 | 20 |
| Центры симметрии | - | 1 | 1 | 1 | 1 |
| Оси симметрии | 3 | 9 | 15 | 9 | 15 |
 |
 |
 |
 |
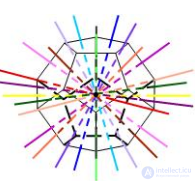 |
|
| Порскости симметрии | 6 | 9 | 15 | 9 | 15 |
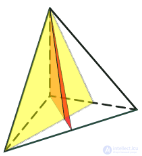 |
|
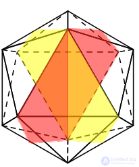 |
|
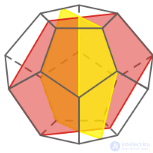 |
|
| Развертки | 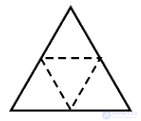 |
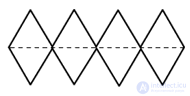 |
 |
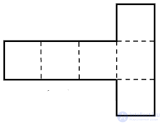 |
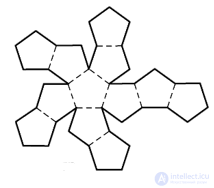 |
Теорема Эйлера Вершины + Грани - Ребра = 2.
Следующий серьезный шаг в науке о многогранниках был сделан в XVIII веке Леонардом Эйлером (1707-1783), который без преувеличения «проверил алгеброй гармонию». Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г. в «Записках Петербургской академии наук», окончательно навела математический порядок в многообразном мире многогранников.
Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника здесь понимается выполнение отдельных движений в определенном заранее установленном порядке. Например, упоминавшийся выше поворот на угол 360/n градусов вокруг прямой a есть произведение отражений относительно любых двух плоскостей, содержащих a и образующих относительно друг друга угол в 180/n градусов. (см. рис 10).
Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким образом, любой поворот вокруг прямой – прямая симметрия. Любое отражение есть обратная симметрия.

Рисунок 11
Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра.
Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии.
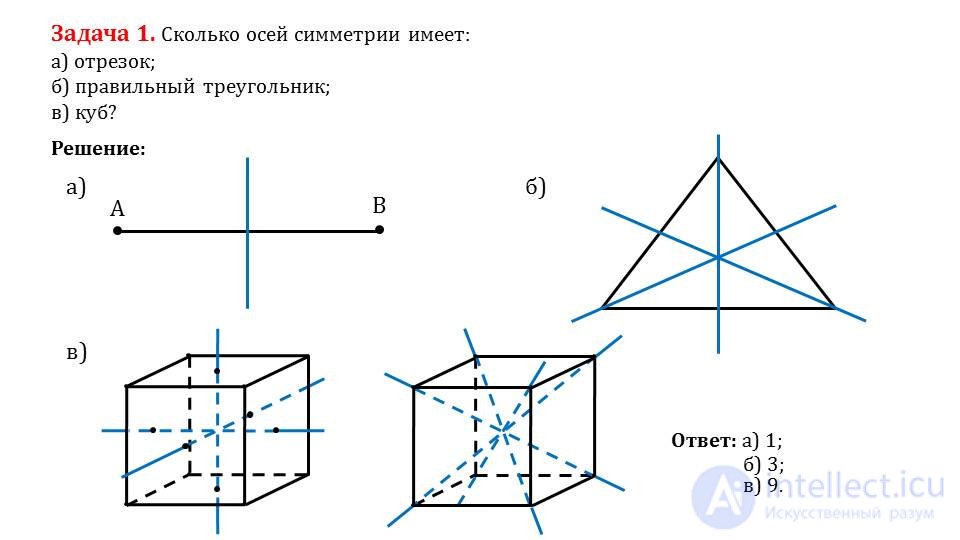
Сколько осей симметрии имеет отрезок, правильный треугольник, куб?
Я что-то не договорил про центральная симметрия параллелепипеда, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое центральная симметрия параллелепипеда, симметрия параллелепипеда, симметрия куба, осевая симметрия параллелепипеда, симметрия многогранников и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Из статьи мы узнали кратко, но содержательно про центральная симметрия параллелепипеда
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия