Привет, сегодня поговорим про площадь сферы, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
площадь сферы , настоятельно рекомендую прочитать все из категории Стереометрия.
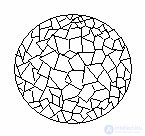
Опишем около сферы выпуклый многогранник с малыми гранями. Пусть S` - площадь поверхности многогранника, т.е. сумма площадей его граней. Найдем приближенное значение площади поверхности многогранника, предполагая, что линейные размеры граней, т.е. расстояние между любыми двумя точками любой грани, меньше ε.
Объем многогранника равен сумме объемов пирамид, имеющих своими основаниями грани многогранника, а вершиной – центр сферы. Об этом говорит сайт https://intellect.icu . Так как все пирамиды имеют одну и ту же высоту, равную радиусу R сферы, то объем многогранника
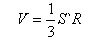
Объем многогранника больше объема шара, ограниченного сферой, но меньше объема шара с тем же центром и с радиусом R+ε. Таким образом,
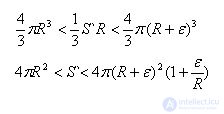
Площадь поверхности описанного многогранника при неограниченном уменьшении размеров его граней, т.е. при неограниченном уменьшении ε, стремится к 4πR^2 и поэтому эта величина принимается за
площадь сферы .
Площадь сферы радиуса R вычисляется по формуле
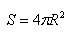
Аналогично определяется площадь сферической части поверхности шарового сектора, т.е. площадь сферического сегмента, для нее получается формула
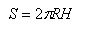
где H – высота сегмента.
Я что-то не договорил про площадь сферы, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое площадь сферы
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Стереометрия
Из статьи мы узнали кратко, но содержательно про площадь сферы

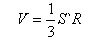
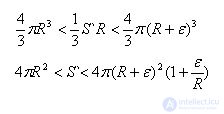
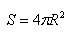
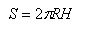
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия