Лекция
Система аксиом стереометрии состоит из аксиом планиметрии и 3 следующих:
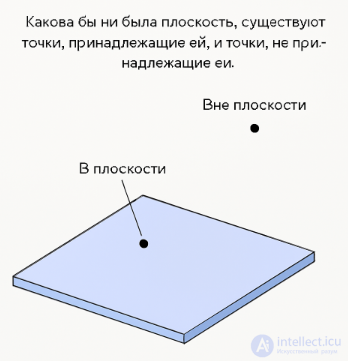
1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
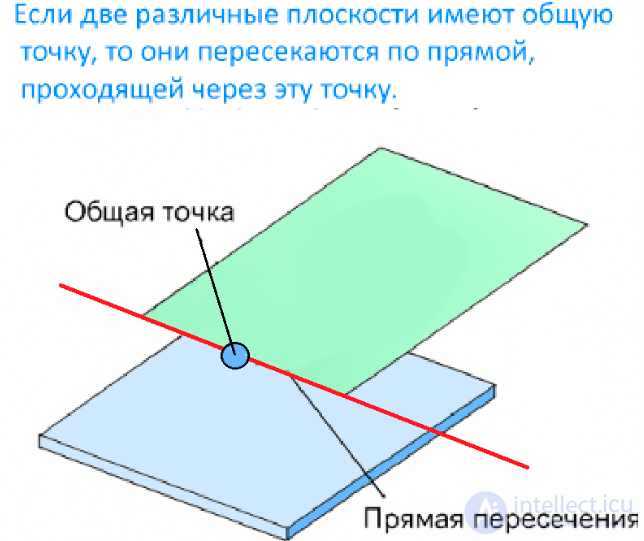
2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
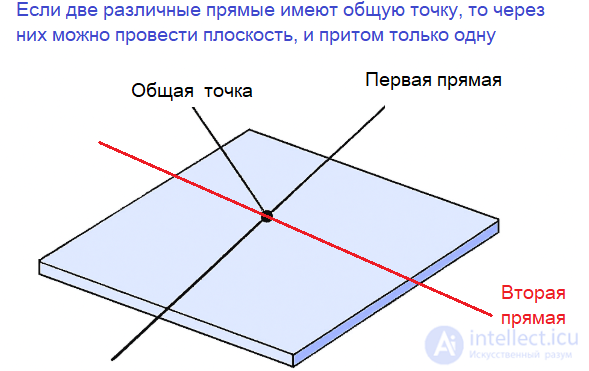
3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Стереометрия — это раздел геометрии, изучающий фигуры в пространстве. Ее аксиоматика развивалась как расширение планиметрии (геометрии на плоскости), начиная с трудов Евклида в «Началах» (~300 г. до н.э.). Однако:
Евклид не формулировал аксиомы стереометрии отдельно — они были имплицитны.
В XIX веке, с развитием аксиоматического метода (Гильберт, Пеано), появилась необходимость строго отделить аксиомы пространства от аксиом плоскости.
Современная система аксиом стереометрии — это логическое расширение планиметрии, добавляющее минимальный набор утверждений, необходимых для описания трехмерного пространства.
Вот как можно интерпретировать три аксиомы стереометрии:
Какова бы ни была плоскость, существуют точки, принадлежащие ей, и точки, не принадлежащие ей.
Это аксиома трехмерности: она утверждает, что пространство не сводится к одной плоскости.
Без нее все было бы двумерным — как лист бумаги.
Она гарантирует наличие «глубины» — третьего измерения.
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Это аксиома структуры пересечения: она описывает, как плоскости взаимодействуют.
Общая точка → общая прямая. Это важно для построений, доказательств и понимания геометрических конфигураций.
Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Это аксиома единственности плоскости, проходящей через две пересекающиеся прямые.
Она позволяет строить плоскости по заданным элементам и гарантирует однозначность.
Стереометрия и ее аксиомы лежат в основе множества дисциплин и практик:
| Область | Применение |
|---|---|
| Архитектура и строительство | Расчет объемов, углов, пересечений конструкций |
| Инженерия и машиностроение | Моделирование деталей, пространственные допуски |
| Химия и кристаллография | Пространственная структура молекул и решеток |
| Компьютерная графика и Игры | 3D-моделирование, рендеринг, пересечения объектов |
| Математика и образование | Формирование пространственного мышления |
| Аэрокосмические технологии | Траектории, ориентация объектов в пространстве |
Вот несколько стратегий:
Визуализируй: рисуй схемы, представляй плоскости и точки в пространстве.
Сравни с планиметрией: ищи аналогии и различия.
Применяй на практике: решай задачи, строй модели, работай с CAD-системами.
Размышляй логически: аксиомы — это фундамент, из которого выводятся теоремы. Понимание их роли — ключ к глубинному мышлению.
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия