Уравнение в математике

Сразу хочу сказать, что здесь никакой воды про уравнение в ма тике , и только нужная информация. Для того чтобы лучше понимать что такое уравнение в ма тике , настоятельно рекомендую прочитать все из категории введение в математику. основы.

 

Первое печатное появление знака равенства в книге Роберта Рекорда в 1557 году (записано уравнение )

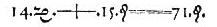
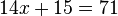Уравне́ние — это равенство вида

Чаще всего в качестве 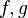 выступают числовые функции, хотя на практике встречаются и более сложные случаи — например, уравнения для вектор-функций, функциональные уравнения и др.

Решение уравнения

 

Иллюстрация графического метода нахождения корней уравнения 

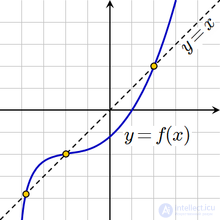
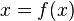
Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).

Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными».

Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.

Про корни говорят, что они удовлетворяют данному уравнению.

Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.

Равносильные уравнения

Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней.

Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.

Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения.

Третье важное свойство задается теоремой: если функции 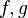 заданы над областью целостности, то уравнение

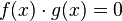
эквивалентно совокупности уравнений:

Это означает, что все корни первого уравнения являются корнями одного из двух других уравнений и позволяет находить корни частями.

Основные свойства

С алгебраическими выражениями, входящими в уравнения, можно выполнять операции, которые не меняют его корней, в частности:

1. В любой части уравнения можно раскрыть скобки.
2. В любой части уравнения можно привести подобные слагаемые.
3. Любой член уравнения можно перенести из одной части в другую, заменив его знак на противоположный.
4. К обеим частям уравнения можно прибавить одно и то же выражение.
5. Из обеих частей уравнения можно вычесть одно и то же выражение.
6. Обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля.

Уравнения, которые являются результатом этих операций, являются эквивалентными начальному уравнению. Однако для свойств 4 и 5 существует ограничение: в случае прибавления к обеим частям уравнения одного и того же выражения (или в случае вычитания из обеих частей уравнения одного и того же выражения), содержащего неизвестное и теряющего смысл при неизвестном, принимающем значения корней данного уравнения, получится уравнение, неэквивалентное исходному (начальному). Но если к обеим частям уравнения прибавить одно и то же выражение (или из обеих частей уравнения вычесть одно и то же выражение), содержащее неизвестное и теряющее смысл лишь при значениях неизвестного, не являющихся корнями данного уравнения, то получится уравнение, эквивалентное начальному.

Умножение или деление обеих частей уравнения на выражение, содержащее неизвестное, может привести, соответственно, к появлению посторонних корней или к потере корней.

Возведение обеих частей уравнения в квадрат может привести к появлению посторонних корней.

Следствие уравнения и посторонние корни

Уравнение

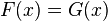
называется следствием уравнения

,

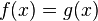если все корни второго уравнения являются корнями первого. Первое уравнение может иметь дополнительные корни, которые для второго уравнения называются посторонними. Посторонние корни могут появиться при преобразованиях, необходимых для нахождения корней уравнений. Для того чтобы их обнаружить, необходимо проверить корень подстановкой в исходное уравнение. Если при подстановке уравнение становится тождеством, то корень настоящий, если нет — посторонний.

Пример

Уравнение

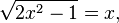
при возведении обеих частей в квадрат дает уравнение

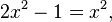 или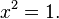 

Оба уравнения являются следствием исходного. Последнее из них легко решить. Оно имеет два корня

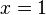 и .

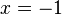При подстановке первого корня в исходное уравнение образуется тождество

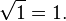
При подстановке другого корня получается неправильное утверждение :

.

Таким образом, второй корень нужно отбросить, как посторонний.

Виды уравнений

Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.

Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни , а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.

К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвертой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвертой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.

Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.

В общем случае, когда аналитического решения найти не удается, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определенного заранее заданного значения.

Алгебраические уравнения

Алгебраическим уравнением называется уравнение вида

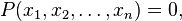
где 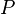 — многочлен от переменных 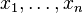, которые называются неизвестными.

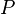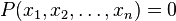Коэффициенты многочлена  обычно берутся из некоторого поля , и тогда уравнение  называется алгебраическим уравнением над полем . Степенью алгебраического уравнения называют степень многочлена .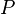

Например, уравнение

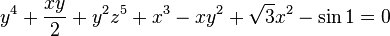
является алгебраическим уравнением седьмой степени от трех переменных (с тремя неизвестными) над полем вещественных чисел.

Линейные уравнения

• в общей форме: 
• в канонической форме: 

Квадратные уравнения

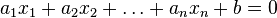
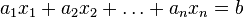
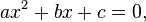
где 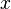 — свободная переменная, 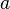, , 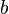 — коэффициенты, причем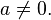 

Выражение 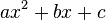 называют квадратным трехчленом. Корень такого уравнения (корень квадратного трехчлена) — это значение переменной 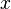, обращающее квадратный трехчлен в нуль, то есть значение, обращающее квадратное уравнение в тождество. Коэффициенты квадратного уравнения имеют собственные названия: коэффициент  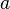называютпервым или старшим, коэффициент  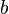называют вторым или коэффициентом при 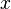,  называется свободным членомэтого уравнения. Приведенным называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент 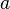:  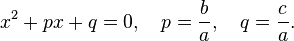Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля. Неполным квадратным уравнением называется такое, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю. Графиком квадратичной функции является парабола.

Для нахождения корней квадратного уравнения  в общем случае следует пользоваться приводимым ниже алгоритмом:

Вычислить значение дискриминанта квадратного уравнения: таковым для него называется выражение .

1)если	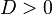2) если	3)если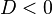
корней два, для отыскания используют формулу: 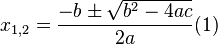,	корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях - его, к тому же, называют корнем кратности 2), формула которого -	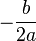делают вывод о том, что корней на множестве действительных чисел нет.

Кубические уравнения

 

График кубической функции

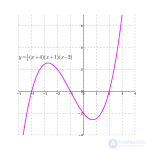
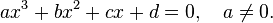
Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола .

Любое кубическое уравнение канонического вида можно привести к более простому виду:

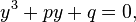
поделив его на 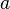 и подставив в него замену  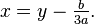При этом коэффициенты будут равны:

Уравнение четвертой степени

 

График многочлена4-ой степени с четырьмя корнями и тремякритическими точками.

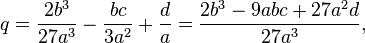
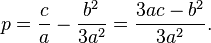
Четвертая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Так как  является многочленом четной степени , она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если 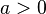, то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если, то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум.

Системы линейных алгебраических уравнений

Система уравнений вида:

Здесь 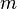 — количество уравнений, а  — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[1].

Система называется однородной, если все ее свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной. Система называется квадратной, если число m уравнений равно числу n неизвестных. Решение системы — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему обращает все ее уравнения в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы называются различными, если нарушается хотя бы одно из равенств:

Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределенной.

Уравнения с параметрами

Уравнением с параметрами называется математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров. Решить уравнение с параметром означает:

1. Найти все системы значений параметров, при которых данное уравнение имеет решение.
2. Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.

Уравнения с параметром могут быть как линейными, так и нелинейными.

Пример линейного уравнения с параметром:

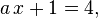
Пример нелинейного уравнения с параметром:

где 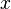 — независимая переменная  — параметр.

Трансцендентные уравнения

Трансцендентным уравнением называется уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции , например:

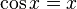
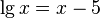
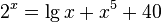
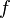Более строгое определение таково: трансцендентное уравнение — это уравнение вида , где функции  и 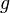 являются аналитическими функциями, и по крайней мере одна из них не является алгебраической.

Функциональные уравнения

Функциональным уравнением называется уравнение, выражающее связь между значением функции (или функций) в одной точке с ее значениями в других точках. Многие свойства функций можно определить, исследуя функциональные уравнения, которым эти функции удовлетворяют. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Например:

• функциональному уравнению

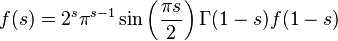
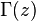где  — Гамма-функция Эйлера, удовлетворяет  Дзета-функция Римана  ζ.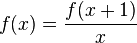

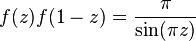• Следующим трем уравнениям удовлетворяет Гамма-функция. Гамма-функция является единственным решением этой системы трех уравнений:

       (формула дополнения Эйлера)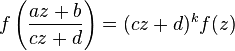

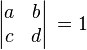• Функциональное уравнение

где a, b, c, d являются целыми числами, удовлетворяющими равенству ad − bc = 1, то есть , определяет f как модулярную форму порядка k.

Дифференциальные уравнения

Дифференциальным уравнением называется уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение ее производныхразличных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные. Порядок дифференциального уравнения — наибольший порядок производных, входящих в него. Решением дифференциального уравнения порядка n называетсяфункция y(x), имеющая на некотором интервале (a, b) производные 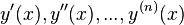 до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием.

Все дифференциальные уравнения можно разделить на

• обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента:

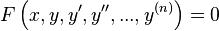 или ,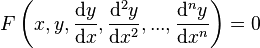

где  — неизвестная функция (возможно,  вектор -функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной 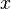, штрих означает дифференцирование по .

• и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных:

,

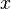где 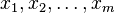 — независимые переменные , а  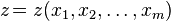— функция этих переменных.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции  времени.

Примеры уравнений

• 
• 
• 
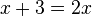
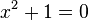
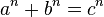• , где 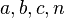 — натуральные числа

Вау!! 😲 Ты еще не читал? Это зря!

• Линейное уравнение
• Квадратное уравнение
• Решение какого-либо уравнения построением
• Система уравнений
• Переменная

Примечания

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про уравнение в ма тике Надеюсь, что теперь ты понял что такое уравнение в ма тике и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории введение в математику. основы