Кубическое уравнение решение и практические применения

Привет, сегодня поговорим про кубическое уравнение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое кубическое уравнение , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.

ax³ + bx² + cx + d = 0. - кубическое уравнение .

График кубической функции , у которой 3 действительных корня (в месте пересечения горизонтальной оси, где у = 0). Имеются 2 критические точки

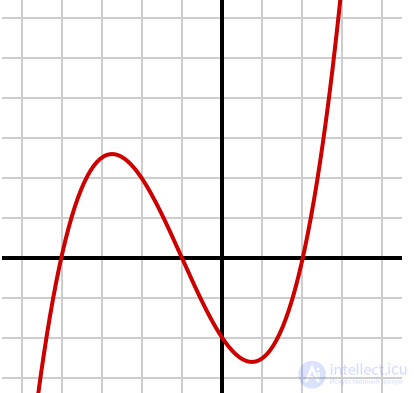
Решение кубического уравнения:

Общие точные методы решения:

• Формула Кардано
• Тригонометрическая формула Виета
• Преобразование Чирнгауза

Для некоторых особых типов кубических уравнений существуют специальные методы решения. См., например:

• Возвратное уравнение
• Теорема Безу

Также можно применять численные методы решения уравнений.

1. Решение Кардано.

Корни неполного кубического уравнения
y³+py+q=0
выражаются формулами:


где
,

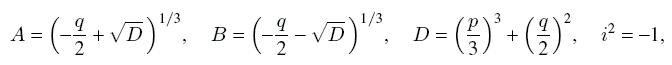причем А и B значения соответсвующих корней, например AB= -p/3.

Число действительных корней кубического уравнения зависит от знака дискриминанта D:

D > 0 - один действительный корень и два сопряженных комплексных корня.

D < 0 - три действительных корня.

D = 0 - один однократный действительный корень и два двукратных, или, если p = q = 0, то один трехкратный действительный корень.

2. Тригонометрическое решение

Если коэффициенты p и q неполного кубического уравнения действительные, то его корни могут быть выражены через тригонометрические функции:

а) Пусть p < 0 и D < 0, тогда



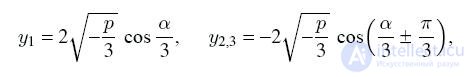
, где тригонометрические функции выражаются так:



б) Пусть p > 0 и D ≥ 0, тогда



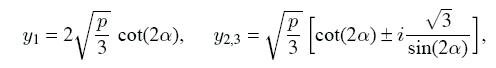
где тригонометрические функции выражаются так:



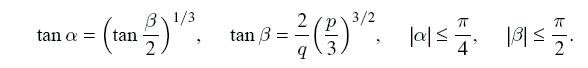
в) Пусть p < 0 и D ≥ 0, тогда:



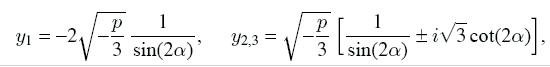
где тригонометрические функции выражаются так:



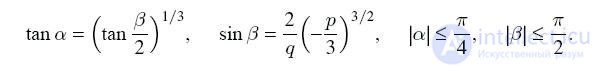
Во всех этих случаях, берутся действительные значения кубических корней.

3. Корни кубического уравнения ax³+bx²+cx+d=0 выражаются формулами:



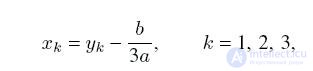
где y_k это корни неполного кубического уравнения с коэффициентами:



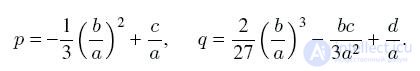
Теорема Виета для корней полного кубического уравнения:

Кубические уравнения были известны еще древним египтянам, вавилонянам, древним грекам, китайцам и индийцам . Были найдены клинописные таблички Старовавилонского периода (XX—XVI век до н. э.), содержащие таблицы значений кубов и кубических корней . Вавилоняне могли использовать эти таблицы для решения кубических уравнений, но не существует никаких свидетельств, что они это делали .

Задача удвоения куба использует простейшее и наиболее старое из кубических уравнений, и древние египтяне не верили, что решение его существует . В пятом веке до нашей эры Гиппократ свел эту задачу к нахождению двух средних пропорциональных между одним отрезком и другим, вдвое большим его, но не смог решить ее с помощью циркуля и линейки , что, как теперь известно, невозможно сделать.

В III веке нашей эры древнегреческий математик Диофант нашел целые и рациональные решения для некоторых кубических уравнений с двумя неизвестными (диофантовых уравнений) . Считается, что Гиппократ, Менехм и Архимед подошли ближе к решению задачи об удвоении куба с помощью конических сечений , хотя некоторые историки, такие как Ревиэль Нетц (Reviel Netz), говорят о том, что неизвестно, думали ли греки о кубических уравнениях, или просто о задачах, которые могут привести к кубическим уравнениям. Другие, как, например, Томас Хит, переводчик и комментатор всех дошедших до нас трудов Архимеда, не соглашаются, указывая на свидетельства, что Архимед действительно решал кубические уравнения с помощью пересечения двух конусов .

Численные методы решения кубических уравнений появляются в китайском математическом тексте Математика в девяти книгах, составленном около второго столетия до нашей эры и прокомментированном китайским математиком Лю Хуэем в третьем столетии .

В VII веке во времена династии Тан астроном и математик Ван Сяотун в своем математическом трактате, озаглавленном Цзигу Суаньцзин, изложил и решил 25 кубических уравнений вида x3+px2+qx=N, в 23 из которых p,q≠0, и в двух уравнениях q=0 .

В XI веке персидский поэт и математик Омар Хайям (1048—1131) сделал существенный прогресс в теории кубических уравнений. Об этом говорит сайт https://intellect.icu . В ранних работах, посвященных кубическим уравнениям, он обнаружил, что кубическое уравнение может иметь два решения (случай трех корней остался им незамеченным ), и утверждал, что уравнение не может быть решено с помощью циркуля и линейки. Он также нашел геометрическое решение . В его более позднем труде, Трактат о демонстрации задач алгебры, он описал полную классификацию кубических уравнений с их общими геометрическими решениями, использующими пересечения конических сечений .

В XII столетии индийский математик Бхаскара II пытался решать кубические уравнения без особых успехов. Однако он привел один пример решения кубического уравнения :

В том же XII столетии персидский математик Шараф ад-Дин написал Al-Mu’adalat (Трактат об уравнениях), в котором говорится о восьми типах кубических уравнений с положительными решениями и о пяти типах, не имеющих положительных решений. Он использовал подход, который позднее стал известен как метод «Руффини — Горнера» для численной аппроксимации корня кубического уравнения. Он разработал также концепцию производной функции и экстремумов кривой для решения кубических уравнений, которые могут не иметь положительных значений . Он понял важность дискриминанта кубического уравнения для нахождения алгебраического решения некоторых специальных видов кубических уравнений .

В средневековой Европе до XVI века успехов в решении кубических уравнений не было. Леонардо Пизанский, известный также как Фибоначчи (1170—1250), умел находить положительные решения кубического уравнения с помощью вавилонских цифр. Он указал решение 1,22,7,42,33,4,40, что равно в стандартной записи и отличается от точного решения только на три триллионных .

Лука Пачоли в своем трактате «Сумма арифметики, геометрии, отношений и пропорций» (1494 год) писал, что общее решение кубических уравнений «столь же невозможно при современном состоянии науки, как и решение квадратуры круга циркулем и линейкой» .

В начале XVI века итальянский математик Сципион дель Ферро нашел общий метод решения важного класса кубических уравнений, а именно, уравнений вида x3+mx=n с неотрицательными n и m. Фактически все кубические уравнения можно свести к такому виду, если допустить возможность для m и n быть отрицательными, но отрицательные числа в то время еще не считались допустимыми. Дель Ферро держал свое открытие в секрете, пока не рассказал о нем перед своей смертью своему ученику Антонио Фиоре (Antonio Fiore).

Никколо Фонтана Тарталья.

В 1535 году Никколо Тарталья получил две задачи в виде кубических уравнений от Дзуанне да Кои (Zuanne da Coi) и объявил, что он их может решить. Он вскоре получил вызов от Фиоре на математическое соревнование, которое после его завершения стало знаменитым. Каждый из них должен был предложить определенное число задач сопернику для решения. Оказалось, что все задачи, полученные Тартальей, сводились к кубическим уравнениям типа x3+mx=n. Незадолго до истечения срока Тарталье удалось разработать общий метод решения кубических уравнений этого типа (переоткрыв метод дель Ферро), а также обобщить его на два других типа (x3=mx+n и x3+n=mx). После этого он быстро решил все предложенные ему задачи. Фиоре же получил от Тартальи задачи из различных разделов математики, многие из которых оказались ему не под силу; в результате Тарталья выиграл соревнование.

Позднее Джероламо Кардано (1501—1576) неоднократно пытался убедить Тарталья раскрыть секрет решения кубических уравнений. В 1539 году ему это удалось: Тарталья сообщил свой метод, но при условии, что Кардано никому его не откроет до выхода книги самого Тартальи о кубических уравнениях, над которой он работал и где собирался опубликовать метод. Спустя шесть лет Тарталья так и не опубликовал свою книгу, а Кардано, узнав к тому времени о работах Ферро, счел возможным опубликовать метод дель Ферро (с упоминанием имени Тартальи, как независимо его открывшего) в своей книге «Ars Magna» в 1545 году. Кардано оправдывался тем, что обещал не сообщать никому результаты Тартальи, а не дель Ферро. Тем не менее, Тарталья считал, что Кардано нарушил обещание и послал тому вызов на соревнование, который Кардано не принял. Вызов, в конце концов, принял ученик Кардано Лодовико Феррари (1522—1565), и оказался победителем .

Кардано заметил, что метод Тарталья иногда (а именно — при наличии трех действительных корней) требует извлечения квадратного корня из отрицательного числа. Он даже включил вычисления с этими комплексными числами в Ars Magna, но, на самом деле, до конца проблему не понял. Рафаэль Бомбелли изучал эту проблему детально, а потому считается первооткрывателем комплексных чисел.

Франсуа Виет (1540—1603) независимо вывел решение кубического уравнения с тремя действительными корнями. Его решение было основано на тригонометрической формуле

В частности, подстановка x=2⋅a⋅cos⁡ϕ приводит уравнение

к виду

Позднее Рене Декарт (1596—1650) углубил работу Виета .

Практическое примерение кубических уравнений

Кубические уравнения, как и квадратные, имеют множество применений в различных практических задачах и науках, где требуется определить значения переменных, описывающих физические, экономические или технические процессы. Вот некоторые ключевые области, в которых решения кубических уравнений играют важную роль:

1. Физика и механика

• Механика жидкости и газа: Кубические уравнения применяются для расчета фазовых переходов, например, в уравнении Ван-дер-Ваальса, которое описывает поведение реальных газов и включает кубическую зависимость от объема.
• Балансировка и равновесие объектов: В задачах, связанных с балансом сил и равновесием, кубические уравнения возникают при описании моментов инерции или распределении массы вдоль трехмерных тел.

2. Оптика

• Расчет линз и зеркал: В геометрической оптике для расчета сложных оптических систем и анализа света, проходящего через линзы или отражающегося от зеркал, решения кубических уравнений помогают вычислять фокусные расстояния, углы и расстояния.
• Аберрации в линзах: Кубические уравнения также используются для моделирования и минимизации аберраций — искажений изображения, вызванных несовершенством линз или других оптических компонентов.

3. Электротехника

• Анализ колебательных контуров: Кубические уравнения применяются в анализе резонансных частот и амплитудных характеристик сложных колебательных контуров, например, в цепях с нелинейными элементами.
• Переходные процессы: В переходных процессах электрических цепей с нелинейными характеристиками часто возникают кубические зависимости, которые описывают изменение параметров во времени.

4. Экономика и финансы

• Моделирование экономических процессов: В экономике кубические уравнения применяются для анализа кривых предложения и спроса, например, для прогнозирования реакции рынка на изменения цены и объема. Такие уравнения могут описывать более сложные нелинейные зависимости, чем линейные или квадратные модели.
• Максимизация прибыли: В задачах оптимизации, связанных с нахождением точек максимума и минимума, кубические уравнения могут описывать более сложные функции, отражающие многокритериальную зависимость прибыли от параметров производства.

5. Компьютерная графика и анимация

• Базисные сплайны и интерполяция: В 3D-графике кубические уравнения используются для построения кривых и поверхностей, таких как кубические сплайны и кривые Безье, которые помогают плавно моделировать и анимировать объекты.
• Моделирование освещения и теней: Кубические уравнения применяются в расчетах отражения света и создания реалистичных теней, что необходимо для получения естественного внешнего вида объектов на изображении.

6. Астрономия и космическая механика

• Определение орбит и гравитационных взаимодействий: В задачах небесной механики кубические уравнения описывают сложные орбиты и взаимодействия между небесными телами, например, в задачах, связанных с гравитационным влиянием нескольких объектов.
• Расчеты приливных сил: Кубические уравнения помогают моделировать сложные нелинейные процессы, связанные с приливными силами и колебаниями во времени.

7. Химия и термодинамика

• Фазовые переходы и растворимость: Кубические уравнения используются для расчета фазовых равновесий, например, для описания перехода между жидкой и газообразной фазой в сложных смесях.
• Химическая кинетика: В некоторых реакциях с нелинейной зависимостью скорости реакции от концентрации также возникают кубические зависимости, что помогает в прогнозировании времени завершения реакции.

Кубические уравнения помогают решать реальные задачи с нелинейными зависимостями, давая более точное и детализированное понимание поведения сложных систем.

Вау!! 😲 Ты еще не читал? Это зря!

• методы решения систем линейных алгебраических уравнений ,
• квадратное уравнение , ax² + bx + c a ≠ 0 , теорема виета , уравнение второй степени ,
• линейное уравнение ,
• Корень Бринга
• Кубика (плоская алгебраическая кривая 3-го порядка)

Я что-то не договорил про кубическое уравнение, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое кубическое уравнение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА