Лекция
Привет, сегодня поговорим про геометрическое распределение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое геометрическое распределение , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
геометрическое распределение в теории вероятностей — распределение дискретнойслучайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».
Функция вероятности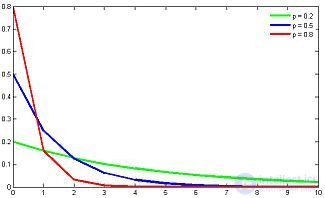 |
||
Функция распределения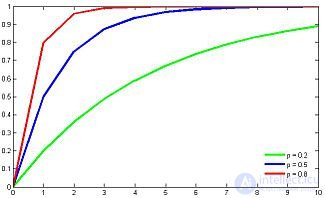 |
||
| Обозначение |  |
|
| Параметры |  —число «неудач» до первого «успеха» —число «неудач» до первого «успеха»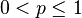 — вероятность «успеха» — вероятность «успеха»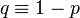 — вероятность «неудачи» — вероятность «неудачи» |
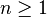 —номер первого «успеха» —номер первого «успеха»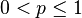 — вероятность «успеха» — вероятность «успеха»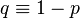 — вероятность «неудачи» — вероятность «неудачи» |
| Носитель | 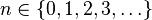 |
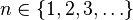 |
| Функция вероятности | 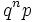 |
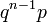 |
| Функция распределения | 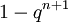 |
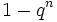 |
| Математическое ожидание | 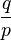 |
 |
| Медиана | N/A | N/A |
| Мода | 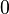 |
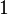 |
| Дисперсия | 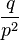 |
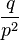 |
| Коэффициент асимметрии |  |
 |
| Коэффициент эксцесса | 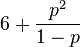 |
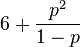 |
| Информационная энтропия | 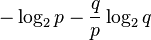 |
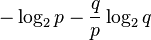 |
| Производящая функция моментов |  |
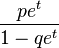 |
| Характеристическая функция | 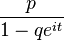 |
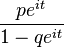 |
Пусть 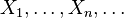 — бесконечная последовательность независимых случайных величин сраспределением Бернулли, то есть
— бесконечная последовательность независимых случайных величин сраспределением Бернулли, то есть
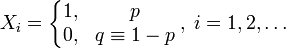
Построим случайную величину 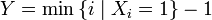 — количество «неудач» до первого «успеха». Об этом говорит сайт https://intellect.icu . Распределение случайной величины
— количество «неудач» до первого «успеха». Об этом говорит сайт https://intellect.icu . Распределение случайной величины 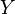 называется геометрическим с вероятностью «успеха»
называется геометрическим с вероятностью «успеха» 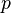 , что обозначается следующим образом:
, что обозначается следующим образом: 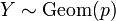 .
.
Функция вероятности случайной величины 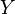 имеет вид:
имеет вид:
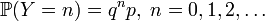
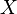 — номер первого «успеха». Тогда функция вероятности принимает форму
— номер первого «успеха». Тогда функция вероятности принимает форму  . В таблице справа приведены формулы для обоих вариантов.
. В таблице справа приведены формулы для обоих вариантов.Производящая функция моментов геометрического распределения имеет вид:
 ,
,
откуда
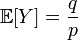 ,
,
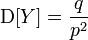 .
.
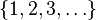 и фиксированным средним
и фиксированным средним 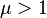 геометрическое распределение
геометрическое распределение 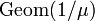 является одним из распределений с максимальной информационной энтропией.
является одним из распределений с максимальной информационной энтропией.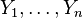 независимы и
независимы и 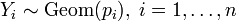 , то
, то .
.
Если 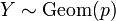 , то
, то  , то есть количество прошлых «неудач» не влияет на количество будущих «неудач».
, то есть количество прошлых «неудач» не влияет на количество будущих «неудач».
Геометрическое распределение — это единственное дискретное распределение со свойством отсутствия памяти.
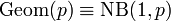 .
.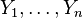 независимы и
независимы и 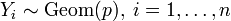 , то
, то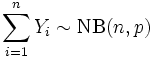 .
.
Пусть игральная кость кидается до выпадания первой шестерки. Тогда вероятность, что нам потребуется не больше трех бросков, равна
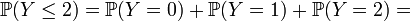
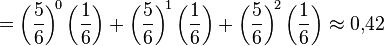 .
.
Ожидаемое число бросков равно
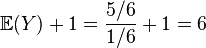 .
.
Геометрический закон распределения имеет место в таких науках как микробиология, генетика, физика. На практике эксперимент или опыт осуществляют до первого появления успешной события А. Число проведенных попыток будет целочисленной случайной величиной 1,2,....Вероятность появления события А в каждом опыте не зависит от предыдущих и составляет p, q=1-p. Вероятности возможных значений случайной величины Х определяется зависимостью
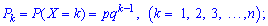
Есть во всех предыдущих опытах кроме k-го експернимент дал плохой результат и только в k-му был успешным. Данную формулу вероятностей называют геометрическим законом распределения, поскольку правая его часть совпадает с выражением общего элемента геометрической прогрессии.
В табличной форме геометрический закон распределения имеет вид

При проверке условия нормировки используется формула суммы бесконечной геометрической прогрессии
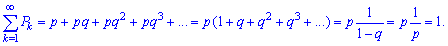
Вероятностную образующую функцию выражаем по формуле
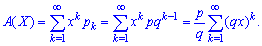
Поскольку 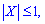 то образующую функцию можно просуммировать
то образующую функцию можно просуммировать
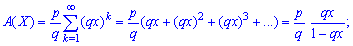
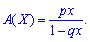
Числовые характеристики для геометрического закона распределения вероятностей определяют по формулам:
1. Математическое ожидание
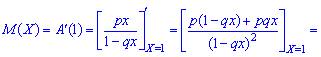
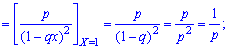
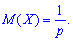
2. Дисперсию и среднее квадратическое отклонение по формулам
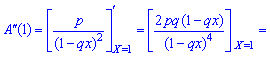
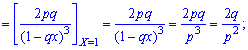
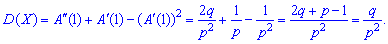
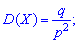

3. Коэффициент асимметрии и эксцесса для геометрического распределения определяют по формуле
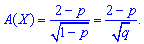
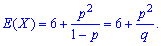
Среди дискретных случайных величин только геометрическому закону дано свойство отсутствия последействия. Это означает, что вероятность появления случайного события в k-ом эксперименте не зависит от того, сколько их появилось до k-го, и всегда равна p.
--------------------------------------
Пример 1. Игральная кость подбрасывается до первого появления цифры 1. Определить все числовые характеристики М (Х), D (X), S (Х), A(X), E(X)для случайной величины Х числа осуществляемых подбрасываний.
Решение. По условию задачи случайная величина Х вляется целочисленной с геометрическим закон распределения вероятностей. Вероятность успешного подбрасывания величина постоянная и равна единице разделенной на количество граней кубика

Имея p,q необходимые числовые характеристики Х находим по приведенным выше формулам
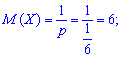
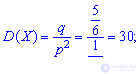
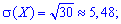

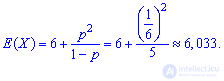
------------------------------------
Пример 2. Охотник-любитель стреляет из ружья по неподвижной мишени. Вероятность попасть в мишень при одном выстреле является величиной постоянной и равна 0,65. Стрельба по мишени ведется до первого попадания.
Определить числовые характеристики М (Х), D (X), S (Х), A(X), E(X) числа израсходованных охотником патронов.
Решение. Случайная величина Х подчиняется геометричниму закона распределения поэтому вероятность попадания в каждой попытке постоянна и составляет p=0,65;q=1-p=0,35.
По формулам вычисляем математическое ожидание
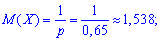
дисперсию
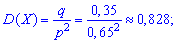
среднее квадратическое отклонение
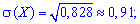
асимметрию
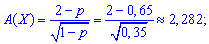
эксцесс
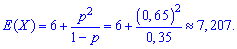
Вычисление числовых характеристик для геометрического закона распределения не так сложны, поэтому пользуйтесь приведенным формулам в подобных задачах и получайте только правильные результаты.
|
Вероятностные распределения
|
||
|---|---|---|
| Дискретные |
|
|
| Абсолютно непрерывные |
|
|
Надеюсь, эта статья про геометрическое распределение, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое геометрическое распределение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про геометрическое распределение
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ