Лекция
Привет, Вы узнаете о том , что такое Вопросы по статистике для специалистов по данным и аналитиков, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Вопросы по статистике для специалистов по данным и аналитиков , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Статистика составляет основу науки о данных или любого анализа в этом отношении. Хорошие знания статистики могут помочь аналитику принимать правильные бизнес-решения.
С одной стороны, описательная статистика помогает нам понять данные и их свойства, используя центральную тенденцию и изменчивость. С другой стороны, логическая статистика помогает нам делать выводы о свойствах совокупности по заданной выборке данных. Знание как описательной, так и логической статистики важно для начинающего специалиста по данным или аналитика.
Чтобы помочь вам улучшить свои знания в области статистики, мы провели этот практический тест. Тест кратко охватывал как описательную, так и логическую статистику. Я даю ответы с пояснениями на тот случай, если вы застряли на определенных вопросах.
Если вы пропустили тест, попробуйте решить вопросы, прежде чем читать решения.
Ниже приведены оценки распределения, они помогут вам оценить вашу производительность.

Вы можете увидеть окончательные результаты здесь . Этот тест прошли более 450 человек, и наивысший результат был 37. Вот несколько статистических данных о распределении.
Средний балл: 20,40
Средний балл: 23
Оценка режима: 25
1) Какие из этих мер используются для анализа основной тенденции данных?
А) Среднее и нормальное распределение
Б) Среднее значение, медиана и мода
C) Режим, Альфа и Диапазон
D) Стандартное отклонение, диапазон и среднее значение
E) Медиана, диапазон и нормальное распределение
Решение: (B)
Среднее значение, медиана и мода - это три статистических показателя, которые помогают нам анализировать центральную тенденцию данных. Мы используем эти меры, чтобы найти центральное значение данных, чтобы обобщить весь набор данных.
2) Дано пять чисел: (5, 10, 15, 5, 15). Теперь, какова будет сумма отклонений отдельных точек данных от их среднего значения?
А) 10
Б) 25
В) 50
Г) 0
E) Ничего из вышеперечисленного
Решение: (D)
Сумма отклонений индивида всегда будет 0.
3) Тест проводится ежегодно. Средний балл теста составляет 150, а стандартное отклонение - 20. Если z-балл Рави равен 1,50, каков его результат на тесте?
A) 180
B) 130
C) 30
D) 150
E) Ничего из вышеперечисленного
Решение: (A)
X = μ + Zσ, где μ - среднее значение, σ - стандартное отклонение, а X - результат, который мы вычисляем. Следовательно, X = 150 + 20 * 1,5 = 180
4) Какой из следующих показателей центральной тенденции всегда будет меняться при изменении одного значения в данных?
А) Среднее
Б) Медиана
C) Режим
D) Все эти
Решение: (A)
Среднее значение набора данных всегда будет изменяться, если мы изменим какое-либо значение набора данных. Поскольку мы суммируем все значения вместе, чтобы получить его, каждое значение набора данных вносит свой вклад в его значение. Медиана и режим могут измениться, а могут и не измениться с изменением одного значения в наборе данных.
5) Ниже мы представили шесть точек данных на шкале, где вертикальные линии на шкале представляют собой единицы.
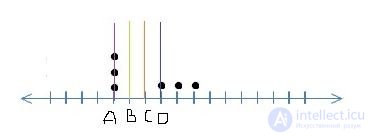
Какая из следующих строк представляет собой среднее значение данных точек данных, где шкала разделена на одинаковые единицы?
А) А
Б) Б
В) В
Г) Г
Решение: (C)
Это немного сложно визуализировать, просто глядя на точки данных. Мы можем просто подставить значения, чтобы понять среднее значение. Пусть A равно 1, B равно 2, C равно 3 и так далее. Показанные значения данных станут {1,1,1,4,5,6}, что будет иметь среднее значение 18/6 = 3, т. Е. C.
6) Если у положительно искаженного распределения медиана 50, какое из следующих утверждений верно?
A) Среднее значение больше 50
B) Среднее значение меньше 50
C) Режим меньше 50
D) Режим больше 50
E) Оба A и C
F) Оба B и D
Решение: (E)
Ниже приведены распределения для отрицательных, положительных и кривых без перекоса.

Как мы видим, для кривой с положительным наклоном Mode
7) Что из следующего является возможным значением медианы приведенного ниже распределения?

А) 32
Б) 26
В) 17
Г) 40
Решение: (B)
Чтобы ответить на этот вопрос, нам нужно перейти к основному определению медианы. Медиана - это значение, которое имеет примерно половину значений перед ним и половину значений после него. Количество значений меньше 25 составляет (36 + 54 + 69 = 159), а количество значений больше 30 (55 + 43 + 25 + 22 + 17 = 162). Таким образом, медиана должна находиться где-то между 25 и 30. Следовательно, 26 - возможное значение медианы.
8) Какие из следующих утверждений относительно поправки Бесселя верны при вычислении стандартного отклонения выборки?
А) Только 2
Б) Только 3
C) И 2, и 3
D) И 1, и 3
Решение: (C)
Вопреки распространенному мнению, исправление Бесселя не всегда следует делать. В основном это делается, когда мы пытаемся оценить стандартное отклонение генеральной совокупности, используя стандартное отклонение выборки. Смещение определенно уменьшается, поскольку стандартное отклонение теперь (после исправления) будет отражать дисперсию совокупности больше, чем дисперсию выборки.
9) Если дисперсия набора данных правильно вычислена по формуле с использованием (n - 1) в знаменателе, какой из следующих вариантов верен?
A) Набор данных - это образец
B) Набор данных - это популяция
C) Набор данных может быть либо выборкой, либо популяцией
D) Набор данных взят из переписи
E) Ничего из вышеперечисленного
Решение: (A)
Если дисперсия имеет значение n-1 в формуле, это означает, что набор является выборкой. Мы пытаемся оценить дисперсию совокупности, разделив сумму квадратов разницы на среднее значение на n-1.
Когда у нас есть фактические данные о населении, мы можем напрямую разделить сумму квадратов разностей на n вместо n-1.
10) [Верно или неверно] Стандартное отклонение может быть отрицательным.
ПРАВДА
Б) ЛОЖЬ
Решение: (B)
Ниже приведена формула стандартного отклонения.
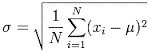
Поскольку разности возводятся в квадрат, складываются и затем укореняются, отрицательные стандартные отклонения невозможны.
11) Стандартное отклонение устойчиво к выбросам?
Правда
Б) Ложь
Решение: (B)
Если вы посмотрите на приведенную выше формулу для стандартного отклонения, очень высокое или очень низкое значение приведет к увеличению стандартного отклонения, так как оно будет сильно отличаться от среднего. Следовательно, выбросы будут влиять на стандартное отклонение.
12) Какой из следующих вариантов верен для приведенного ниже нормального распределения?
σ1, σ2 и σ3 представляют собой стандартные отклонения для кривых 1, 2 и 3 соответственно.
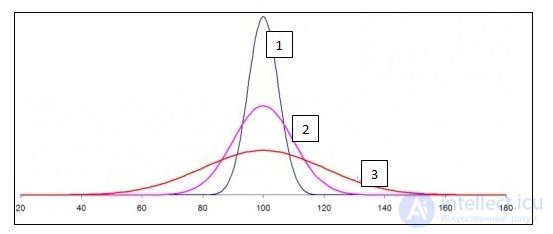
А) σ1> σ2> σ3
Б) σ1 <σ2 <σ3
В) σ1 = σ2 = σ3
D) Нет
Решение: (B)
Из определения нормального распределения мы знаем, что площадь под кривой равна 1 для всех трех форм. Кривая 3 более развернута и, следовательно, более разбросана (большинство значений находится в пределах 40–160). Следовательно, у него будет самое высокое стандартное отклонение. Точно так же кривая 1 имеет очень низкий диапазон, и все значения находятся в небольшом диапазоне 80–120. Следовательно, кривая 1 имеет наименьшее стандартное отклонение.
13) Какими будут критические значения Z для 98% доверительного интервала для двустороннего теста?
A) +/- 2,33
B) +/- 1,96
C) +/- 1,64
D) +/- 2,55
Решение: (A)
Чтобы ответить на этот вопрос, нам нужно взглянуть на таблицу z. Для двухстороннего теста и 98% доверительного интервала мы должны проверить область перед значением z как 0,99, поскольку 1% будет слева от среднего, а 1% - справа. Следовательно, мы должны проверить значение z для области> 0,99. Значение будет +/- 2,33.
14) [Верно или неверно] Стандартная нормальная кривая симметрична относительно 0, а общая площадь под ней равна 1.
ПРАВДА
Б) ЛОЖЬ
Решение: (A)
По определению нормальной кривой площадь под ней равна 1 и симметрична относительно нуля. Об этом говорит сайт https://intellect.icu . Среднее значение, медиана и мода равны и равны 0. Площадь слева от среднего равна площади справа от среднего. Следовательно, он симметричен.
Контекст для вопросов 15-17
Исследования показывают, что прослушивание музыки во время учебы может улучшить вашу память. Чтобы продемонстрировать это, исследователь собирает выборку из 36 студентов колледжа и дает им стандартный тест памяти, пока они слушают фоновую музыку. При нормальных обстоятельствах (без музыки) полученная средняя оценка составляла 25, а стандартное отклонение - 6. Средняя оценка для образца после эксперимента (т.е. с музыкой) составляла 28.
15) Какая в этом случае нулевая гипотеза?
А) Прослушивание музыки во время учебы не влияет на память.
Б) Прослушивание музыки во время учебы может ухудшить память.
В) Прослушивание музыки во время учебы может улучшить память.
Г) Прослушивание музыки во время учебы не улучшит память, но может ухудшить ее.
Решение: (D)
Нулевая гипотеза - это обычно предполагаемое утверждение, что в измеряемых явлениях нет никакой связи. Здесь нулевая гипотеза заключается в том, что нет никакой связи между прослушиванием музыки и улучшением памяти.
16) В чем будет ошибка типа I?
А) Вывод о том, что прослушивание музыки во время учебы улучшает память, и это правильно.
Б) Вывод о том, что прослушивание музыки во время учебы улучшает память, хотя на самом деле это не так.
В) Вывод о том, что прослушивание музыки во время учебы не улучшает память, но улучшает.
Решение: (B)
Ошибка типа 1 означает, что мы отвергаем нулевую гипотезу, когда она действительно верна. Нулевая гипотеза заключается в том, что музыка не улучшает память. Ошибка типа 1 заключается в том, что мы отвергаем ее и говорим, что музыка действительно улучшает память, хотя на самом деле это не так.
17) После проведения Z-теста, что мы можем сделать ____?
А) Прослушивание музыки не улучшает память.
Б) Прослушивание музыки значительно улучшает память на р.
В) Информации недостаточно для вывода.
D) Ничего из вышеперечисленного
Решение: (B)
Давайте выполним Z-тест для данного случая. Мы знаем, что нулевая гипотеза состоит в том, что прослушивание музыки не улучшает память.
Альтернативная гипотеза состоит в том, что прослушивание музыки улучшает память.
В этом случае стандартная ошибка, т.е. 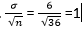
Z-балл для выборочного среднего 28 из этой совокупности составляет

Критическое значение Z для α = 0,05 (одностороннее) будет 1,65, как видно из таблицы z.
Следовательно, поскольку наблюдаемое значение Z больше критического значения Z, мы можем отвергнуть нулевую гипотезу и сказать, что прослушивание музыки действительно улучшает память с достоверностью 95%.
18) На основании своего анализа исследователь заключает, что плацебо лечит СПИД. Какую ошибку он совершает?
А) Ошибка типа 1
Б) Ошибка 2-го типа
C) Ничего из этого. Исследователь не ошибается.
D) Не может быть определено
Решение: (D)
По определению, ошибка типа 1 отвергает нулевую гипотезу, когда она действительно верна, а ошибка типа 2 принимает нулевую гипотезу, когда она фактически ложна. В этом случае для определения ошибки нам нужно сначала определить нулевую и альтернативную гипотезы.
19) Что происходит с доверительным интервалом, когда мы вводим в данные некоторые выбросы?
A) Доверительный интервал устойчив к выбросам
Б) Доверительный интервал увеличится с появлением выбросов.
C) Доверительный интервал уменьшится с появлением выбросов.
Г) В этом случае мы не можем определить доверительный интервал.
Решение: (B)
Мы знаем, что доверительный интервал зависит от стандартного отклонения данных. Если мы вводим выбросы в данные, стандартное отклонение увеличивается, и, следовательно, доверительный интервал также увеличивается.
Контекст для вопросов 20-22
Врач хочет снизить уровень сахара в крови всех своих пациентов, изменив их диету. Он обнаружил, что средний уровень сахара у всех пациентов составляет 180 со стандартным отклонением 18. Девять из его пациентов переходят на диету, и среднее значение выборки составляет 175. Теперь он рассматривает возможность рекомендовать всем своим пациентам перейти на диету. рацион питания.
Примечание: он рассчитывает доверительный интервал 99%.
20) Что такое стандартная ошибка среднего?
А) 9
Б) 6
В) 7,5
Г) 18
Решение: (B)
Стандартная ошибка среднего - это стандартное отклонение квадратным корнем из числа значений. т.е.
Стандартная ошибка = 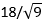 = 6
= 6
21) Какова вероятность получить среднее значение 175 или меньше после того, как все пациенты начнут соблюдать диету?
А) 20%
Б) 25%
В) 15%
Г) 12%
Решение: (A)
Это на самом деле хочет, чтобы мы вычислили вероятность того, что среднее значение популяции будет 175 после вмешательства. Мы можем вычислить значение Z для данного среднего значения.

Если мы посмотрим на таблицу z, соответствующее значение для z = -0,833 ~ 0,2033.
Следовательно, существует около 20% вероятности, что если все начнут сидеть на диете, среднее значение для населения будет 175.
22) Какое из следующих утверждений верно?
А) У врача есть веские доказательства того, что диета снижает уровень сахара в крови.
Б) У врача недостаточно доказательств того, что соблюдение диеты снижает уровень сахара в крови.
В) Если врач назначит для всех будущих пациентов одинаковую диету, среднее артериальное давление упадет ниже 160.
Решение: (B)
Нам нужно проверить, достаточно ли у нас доказательств, чтобы отклонить нулевое значение. Нулевая гипотеза состоит в том, что диета не влияет на уровень сахара в крови. Это двусторонний тест. Критическое значение z для двухстороннего теста будет ± 2,58.
Значение z, как мы рассчитали, составляет -0,833.
Поскольку значение Z <критического значения Z, у нас недостаточно доказательств того, что диета снижает уровень сахара в крови.
Контекст вопроса 23-25
Исследователь пытается изучить влияние двух разных методов обучения. Он делит 20 студентов на две группы по 10 человек в каждой. Для группы 1 метод обучения использует забавные примеры. Что касается группы 2, метод обучения заключается в использовании программного обеспечения, помогающего студентам учиться. После 20-минутной лекции обеих групп для всех студентов проводится тест.
Мы хотим вычислить, есть ли значительная разница в оценках обеих групп.
Принято, что:
23) Какое значение имеет t-статистика?
A) 3,191
B) 3,395
C) Не может быть определено.
D) Ничего из вышеперечисленного
Решение: (A)
Статистика t данной группы есть не что иное, как разница между средними значениями группы по стандартной ошибке.
= (10-7) /0,94 = 3,191
24) Есть ли существенная разница в оценках двух групп?
А) Да
Б) Нет
Решение: (A)
Нулевая гипотеза в этом случае будет заключаться в том, что между группами нет разницы, в то время как альтернативная гипотеза будет заключаться в том, что группы существенно различаются.
Критическое значение t для двухстороннего теста при α = 0,05 составляет ± 2,101. Полученная статистика t равна 3,191. Поскольку t-статистика превышает критическое значение t, мы можем отвергнуть нулевую гипотезу и сказать, что две группы значительно различаются с достоверностью 95%.
25) Какой процент вариативности в оценках объясняется методом обучения?
А) 36,13
Б) 45,21
В) 40,33
Г) 32,97
Решение: (A)
% Изменчивости оценок определяется значением R 2 . Формула для R 2 определяется как
R 2 = 
Степени свободы в этом случае будут 10 + 10 -2, так как есть две группы размером 10 каждая. Степень свободы 18.
R 2 = 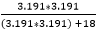 = 36,13
= 36,13
26) [Верно или неверно] Статистика F не может быть отрицательной.
ПРАВДА
Б) ЛОЖЬ
Решение: (A)
F-статистика - это значение, которое мы получаем, когда запускаем тест ANOVA для разных групп, чтобы понять различия между ними. Статистика F определяется отношением межгрупповой изменчивости к внутригрупповой изменчивости.
Ниже приведена формула для статистики f.
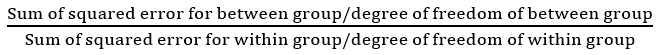
Поскольку и числитель, и знаменатель содержат квадратные члены, статистика F не может быть отрицательной.
27) Какой из приведенных ниже графиков имеет очень сильную положительную корреляцию?
А) Б) В) Г)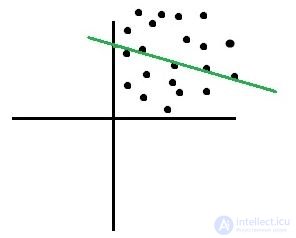
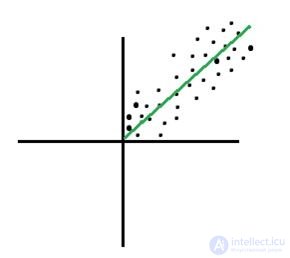
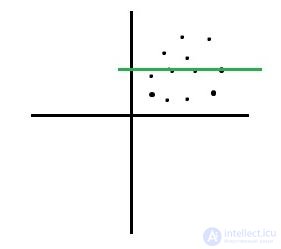
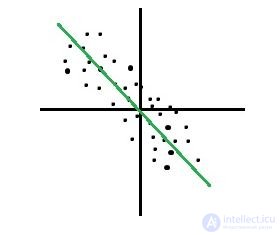
Решение: (B)
Сильная положительная корреляция будет иметь место при выполнении следующего условия. Если x увеличивается, y должен также увеличиваться, если x уменьшается, y также должен уменьшаться. В этом случае наклон линии будет положительным, а точки данных покажут четкую линейную зависимость. Вариант B показывает сильные положительные отношения.
28) Корреляция между двумя переменными (Var1 и Var2) составляет 0,65. Теперь, после добавления числа 2 ко всем значениям Var1, коэффициент корреляции будет _______?
A) Увеличение
B) Уменьшение
C) Ничего из вышеперечисленного
Решение: (C)
Если к любой переменной добавляется или вычитается постоянное значение, коэффициент корреляции не изменяется. Это легко понять, если посмотреть на формулу для расчета корреляции.
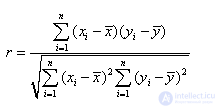
Если мы добавим постоянное значение ко всем значениям x, x i и изменится на одно и то же число, а различия останутся прежними. Следовательно, коэффициент корреляции не меняется.
29) Замечено, что существует очень высокая корреляция между результатами тестов по математике и количеством физических упражнений, выполненных студентом в день теста. Что из этого можно сделать?
A) Только 1
B) 1 и 3
C) 2 и 3
D) Все утверждения верны
Решение: (C)
Хотя иногда причинно-следственная связь может быть интуитивно понятной из-за высокой корреляции, на самом деле корреляция не подразумевает каких-либо причинных выводов. Это просто говорит нам о силе связи между двумя переменными. Если обе переменные движутся вместе, между ними существует высокая корреляция.
30) Если коэффициент корреляции (r) между результатами теста по математике и количеством физических упражнений учащимся составляет 0,86, какой процент вариабельности в тесте по математике объясняется количеством упражнений?
А) 86%
Б) 74%
В) 14%
Г) 26%
Решение: (B)
% Изменчивости выражается квадратом коэффициента корреляции r 2 . Это значение представляет собой долю вариации одной переменной, которая может быть объяснена другой переменной. Следовательно,% объясненной изменчивости будет 0,86 2 .
31) Что из следующего верно относительно данной гистограммы?

A) Гистограмма выше одномодальная
Б) Гистограмма выше двухрежимная.
C) Данные выше не являются гистограммой
D) Ничего из вышеперечисленного
Решение: (B)
Приведенная выше гистограмма двухрежимная. Как мы видим, есть два значения, для которых мы можем видеть пики на гистограммах, указывающие на высокие частоты для этих значений. Следовательно, гистограмма бимодальная.
32) Рассмотрим линию регрессии y = ax + b, где a - наклон, а b - точка пересечения. Если мы знаем значение наклона, то с помощью какого параметра мы всегда можем найти значение точки пересечения?
A) Поместите значение (0,0) в линию регрессии True
B) Поместите любое значение из точек, используемых для соответствия линии регрессии, и вычислите значение b False
C) Поместите средние значения x и y в уравнение вместе со значением a, чтобы получить b False
D) Ничего из вышеперечисленного нельзя использовать. Ложь.
Решение: (C)
В случае обычной регрессии методом наименьших квадратов линия всегда будет проходить через средние значения x и y. Если мы знаем одну точку на линии и значение наклона, мы можем легко найти точку пересечения.
33) Что происходит, когда мы вводим больше переменных в модель линейной регрессии?
A) Значение r в квадрате может увеличиваться или оставаться постоянным, скорректированное значение r в квадрате может увеличиваться или уменьшаться.
Б) Квадрат r может увеличиваться или уменьшаться, в то время как скорректированный квадрат r всегда увеличивается.
C) Как квадрат r, так и скорректированный квадрат r всегда увеличиваются при введении новых переменных в модель.
D) Оба значения могут увеличиваться или уменьшаться в зависимости от введенных переменных.
Решение: (A)
R-квадрат всегда увеличивается или, по крайней мере, остается постоянным, потому что в случае обычных наименьших квадратов сумма квадратичной ошибки никогда не увеличивается при добавлении дополнительных переменных в модель. Следовательно, R в квадрате не уменьшается. Скорректированный R-квадрат - это модифицированная версия R-квадрата, скорректированная с учетом количества предикторов в модели. Скорректированный R-квадрат увеличивается только в том случае, если новый член улучшает модель больше, чем можно было бы ожидать случайно. Он уменьшается, когда предсказатель случайно улучшает модель меньше, чем ожидалось.
34) На диаграмме рассеяния расстояние по вертикали до точки выше или ниже линии регрессии известно как ____?
TODO img A) Остаточный
B) Ошибка предсказания
C) Прогноз
D) И A, и B
E) Ничего из вышеперечисленного
Решение: (D)
Линии, которые мы видим на приведенном выше графике, представляют собой вертикальное расстояние точек от линии регрессии. Они известны как остатки или ошибка предсказания.
35) В одномерной линейной регрессии методом наименьших квадратов связь между коэффициентом корреляции и коэффициентом детерминации составляет ______?
A) Оба не связаны Ложь
Б) Коэффициент детерминации - это квадрат коэффициента корреляции Истина
C) Коэффициент детерминации - это квадратный корень из коэффициента корреляции. Ложь.
D) Оба одинаковые F
Решение: (B)
Коэффициент детерминации - это значение в квадрате R, и он сообщает нам степень изменчивости зависимой переменной, объясняемой независимой переменной. Это не что иное, как квадрат коэффициента корреляции. В случае многомерной регрессии значение r в квадрате представляет собой отношение суммы объясненной дисперсии к сумме общей дисперсии.
36) Какая связь между уровнем значимости и уровнем достоверности?
A) Уровень значимости = Уровень достоверности
B) Уровень значимости = 1 - Уровень достоверности
C) Уровень значимости = 1 / Уровень достоверности
D) Уровень значимости = sqrt (1 - Уровень достоверности)
Решение: (B)
Уровень значимости - 1-доверительный интервал. Если уровень значимости составляет 0,05, соответствующий доверительный интервал составляет 95% или 0,95. Уровень значимости - это вероятность получения результата, такого же или более экстремального, чем результат, фактически полученный, когда нулевая гипотеза верна. Доверительный интервал - это диапазон вероятных значений параметра совокупности, например среднего значения совокупности. Например, если вы вычисляете 95% доверительный интервал для средней цены мороженого, то можете быть на 95% уверены, что этот интервал содержит истинную среднюю стоимость всех мороженых.
Уровень значимости и уровень достоверности являются дополнительными частями нормального распределения.
37) [Верно или неверно] Предположим, вам дана переменная V, а также ее среднее значение и медиана. На основе этих значений вы можете определить, смещена ли переменная «V» влево или вправо для условия.
среднее (V)> медианное (V)
А) Верно
Б) Неверно
Решение: (B)
Поскольку о распределении типов переменной V не упоминается, мы не можем точно сказать, скошен ли он влево или вправо.
38) Линия, описываемая уравнением линейной регрессии (OLS), пытается ____?
А) Пройдите как можно больше точек.
Б) Пройдите как можно меньше очков
C) Минимизируйте количество точек, которых он касается
D) Минимизируйте квадрат расстояния от точек
Решение: (D)
Линия регрессии пытается минимизировать квадрат расстояния между точками и линией регрессии. По определению, обычная регрессия методом наименьших квадратов пытается получить минимальную сумму квадратов ошибок. Это означает, что сумма квадратов остатков должна быть минимизирована. Это может быть достигнуто, а может и не быть достигнуто путем прохождения максимальных точек в данных. Самый распространенный случай, когда не проходят все точки и уменьшается ошибка, - это когда данные имеют много выбросов или не очень сильно линейны.
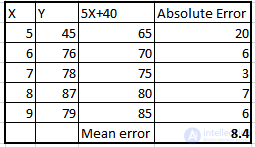
39) У нас есть уравнение линейной регрессии (Y = 5X +40) для приведенной ниже таблицы.
| Икс | Y |
| 5 | 45 |
| 6 | 76 |
| 7 | 78 |
| 8 | 87 |
| 9 | 79 |
Что из следующего является MAE (средней абсолютной ошибкой) для этой линейной модели?
A) 8,4
B) 10,29
C) 42,5
D) Ничего из вышеперечисленного
Решение: (A)
Чтобы вычислить среднюю абсолютную ошибку для этого случая, мы должны сначала вычислить значения y с заданным уравнением, а затем вычислить абсолютную ошибку по отношению к фактическим значениям y. Тогда среднее значение этой абсолютной ошибки будет средней абсолютной ошибкой. В таблице ниже приведены эти значения.
40) Регрессионный анализ веса (y) и роста (x) привел к следующей линии наименьших квадратов: y = 120 + 5x. Это означает, что при увеличении высоты на 1 дюйм вес, как ожидается,
A) увеличение на 1 фунт
B) увеличение на 5 фунтов
C) увеличение на 125 фунтов
D) ничего из вышеперечисленного
Решение: (B)
Глядя на уравнение, получаем y = 120 + 5x. Если рост увеличится на 1 единицу, вес увеличится на 5 фунтов. Так как 120 будет одинаковым в обоих случаях и уйдет в разность.
41) [Верно или неверно] Пирсон фиксирует, насколько линейно зависимы две переменные, тогда как Спирмен фиксирует монотонное поведение отношения между переменными.
ПРАВДА
Б) ЛОЖЬ
Решение: (A)
Утверждение верно. Корреляция Пирсона оценивала линейную связь между двумя непрерывными переменными. Отношение является линейным, когда изменение одной переменной связано с пропорциональным изменением другой переменной.
Копьеносец оценивает монотонность отношений. Монотонная взаимосвязь - это взаимосвязь, при которой переменные изменяются вместе, но не обязательно с постоянной скоростью.
Надеюсь, вам понравилось решать вопросы, и они заставили вас когда-нибудь почесать голову. Поделитесь своими мыслями по вышеуказанным темам, а также своими отзывами.
Будем рады воплотить ваши идеи в следующих статьях и тестах. Кроме того, один вопрос может иметь несколько подходов, а приведенное выше решение может показывать только один. Я попытался описать решения, но не стесняйтесь исследовать дальше в случае сомнений, используя комментарии ниже.
Исследование, описанное в статье про Вопросы по статистике для специалистов по данным и аналитиков, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Вопросы по статистике для специалистов по данным и аналитиков и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ