Лекция
Привет, Вы узнаете о том , что такое сглаживание экспериментальных зависимостей по методу наименьших квадратов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое сглаживание экспериментальных зависимостей по методу наименьших квадратов , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
К вопросам, связанным с обработкой опытов, разобранным в данной главе, близко примыкает вопрос о сглаживании экспериментальных зависимостей.
Пусть производится опыт, целью которого является, исследование зависимости некоторой физической величины  от физической величины
от физической величины  (например, зависимости пути, пройденного телом, от времени; начальной скорости снаряда от температуры заряда; подъемной силы от угла атаки и т. д.). Предполагается, что величины
(например, зависимости пути, пройденного телом, от времени; начальной скорости снаряда от температуры заряда; подъемной силы от угла атаки и т. д.). Предполагается, что величины  и
и  связаны функциональной зависимостью:
связаны функциональной зависимостью:
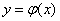 . (14.8.1)
. (14.8.1)
Вид этой зависимости и требуется определить из опыта.
Предположим, что в результате опыта мы получили ряд экспериментальных точек и построили график зависимости  от
от  (рис. 14.8.1). Обычно экспериментальные точки на таком графике располагаются не совсем правильным образом - дают некоторый «разброс», т. е. обнаруживают случайные отклонения от видимой общей закономерности.
(рис. 14.8.1). Обычно экспериментальные точки на таком графике располагаются не совсем правильным образом - дают некоторый «разброс», т. е. обнаруживают случайные отклонения от видимой общей закономерности.

Рис. 14.8.1.
Эти уклонения связаны с неизбежными при всяком опыте ошибками измерения.
Возникает вопрос, как по этим экспериментальным данным наилучшим образом воспроизвести зависимость  от
от  ?
?
Известно, что через любые 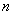 точек с координатами
точек с координатами 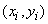 всегда можно провести кривую, выражаемую аналитически полиномом степени
всегда можно провести кривую, выражаемую аналитически полиномом степени 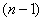 , так, чтобы она в точности прошла через каждую из точек (рис. 14.8.2).
, так, чтобы она в точности прошла через каждую из точек (рис. 14.8.2).

Рис. 14.8.2.
Однако такое решение вопроса обычно не является удовлетворительным: как правило, нерегулярное поведение экспериментальных точек, подобное изображенному на рис. 14.8.1 и 14.8.2, связано не с объективным характером зависимости  от
от  , а исключительно с ошибками измерения. Это легко обнаружить, сравнивая наблюденные уклонения (разброс точек) с примерно известными ошибками измерительной аппаратуры.
, а исключительно с ошибками измерения. Это легко обнаружить, сравнивая наблюденные уклонения (разброс точек) с примерно известными ошибками измерительной аппаратуры.
Тогда возникает весьма типичная для практики задача сглаживания экспериментальной зависимости. Желательно обработать экспериментальные данные так, чтобы по возможности точно отразить общую тенденцию зависимости  от
от  , но вместе с тем сгладить незакономерные, случайные уклонения, связанные с неизбежными погрешностями самого наблюдения.
, но вместе с тем сгладить незакономерные, случайные уклонения, связанные с неизбежными погрешностями самого наблюдения.
Для решения подобных задач обычно применяется расчетный метод, известный под названием «метода наименьших квадратов». Этот метод дает возможность при заданном типе зависимости 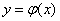 так выбрать ее числовые параметры, чтобы кривая
так выбрать ее числовые параметры, чтобы кривая 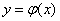 в известном смысле наилучшим образом отображала экспериментальные данные.
в известном смысле наилучшим образом отображала экспериментальные данные.
Скажем несколько слов о том, из каких соображений может быть выбран тип кривой 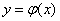 . Часто этот вопрос решается непосредственно по внешнему виду экспериментальной зависимости. Например, экспериментальные точки, изображенные на рис. 14.8.3, явно наводят на мысль о прямолинейной зависимости вида
. Часто этот вопрос решается непосредственно по внешнему виду экспериментальной зависимости. Например, экспериментальные точки, изображенные на рис. 14.8.3, явно наводят на мысль о прямолинейной зависимости вида 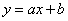 .
.

Рис. 14.8.3.
Зависимость, изображенная на рис. 14.8.4, хорошо может быть представлена полиномом второй степени 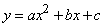 .
.

Рис. 14.8.4.
Если речь идет о периодической функции, часто можно выбрать для ее изображения несколько гармоник тригонометрического ряда и т. д.
Очень часто бывает так, что вид зависимости (линейная, квадратичная, показательная и т. д.) бывает известен из физических соображений, связанных с существом решаемой задачи, а из опыта требуется установить только некоторые параметры этой зависимости.
Задачу о рациональном выборе таких числовых параметров при данном виде зависимости мы и будем решать в настоящем 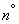 .
.
Пусть имеются результаты 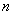 независимых опытов, оформленные в виде простой статистической таблицы (табл. 14.8.1), где
независимых опытов, оформленные в виде простой статистической таблицы (табл. 14.8.1), где 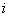 - номер опыта;
- номер опыта; 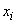 - значение аргумента;
- значение аргумента; 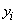 - соответствующее значение функции.
- соответствующее значение функции.
Таблица 14.8.1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точки 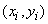 нанесены на график (рис. 14.8.5).
нанесены на график (рис. 14.8.5).
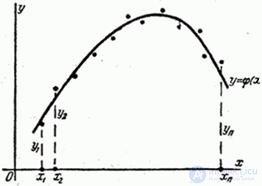
Рис. 14.8.5.
Из теоретических или иных соображений выбран принципиальный вид зависимости 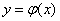 . Функция
. Функция 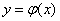 содержит ряд числовых параметров
содержит ряд числовых параметров 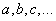 . Требуется так выбрать эти параметры, чтобы кривая
. Требуется так выбрать эти параметры, чтобы кривая 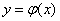 в каком-то смысле наилучшим образом изображала зависимость, полученную в опыте.
в каком-то смысле наилучшим образом изображала зависимость, полученную в опыте.
Решение этой задачи, как и любой задачи выравнивания или сглаживания, зависит от того, что именно мы условимся считать «наилучшим». Можно, например, считать «наилучшим» такое взаимное расположение кривой и экспериментальных точек, при котором максимальное расстояние между ними обращается в минимум; можно потребовать, чтобы в минимум обращалась сумма абсолютных величин отклонений точек от кривой и т. д. При каждом из этих требовании мы получим свое решение задачи, свои значения параметров 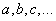 .
.
Однако общепринятым при решении подобных задач является так называемый метод наименьших квадратов, при котором требование наилучшего согласования кривой 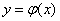 и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум. Метод наименьших квадратов имеет перед другими методами сглаживания существенные преимущества: во-первых. он приводит к сравнительно простому математическому способу определения параметров
и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум. Метод наименьших квадратов имеет перед другими методами сглаживания существенные преимущества: во-первых. он приводит к сравнительно простому математическому способу определения параметров 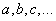 ; во-вторых, он допускает довольно веское теоретическое обоснование с вероятностной точки зрения.
; во-вторых, он допускает довольно веское теоретическое обоснование с вероятностной точки зрения.
Изложим это обоснование. Предположим, что истинная зависимость  от
от  в точности выражается формулой
в точности выражается формулой 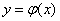 ; экспериментальные точки уклоняются от этой зависимости вследствие неизбежных ошибок измерения. Мы уже упоминали о том, что ошибки измерения, как правило, подчиняются нормальному закону. Допустим, что это так. Рассмотрим какое-нибудь значение аргумента
; экспериментальные точки уклоняются от этой зависимости вследствие неизбежных ошибок измерения. Мы уже упоминали о том, что ошибки измерения, как правило, подчиняются нормальному закону. Допустим, что это так. Рассмотрим какое-нибудь значение аргумента 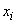 . Результат опыта есть случайная величина
. Результат опыта есть случайная величина 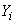 , распределенная по нормальному закону с математическим ожиданием
, распределенная по нормальному закону с математическим ожиданием 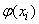 и со средним квадратическим отклонением
и со средним квадратическим отклонением 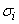 , характеризующим ошибку измерения. Предположим, что точность измерения во всех точках одинакова:
, характеризующим ошибку измерения. Предположим, что точность измерения во всех точках одинакова:
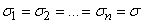 .
.
Тогда нормальный закон, по которому распределяется величина 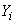 , можно записать в виде:
, можно записать в виде:
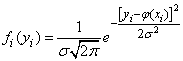 . (14.8.2)
. (14.8.2)
В результате нашего опыта - ряда измерений - произошло следующее событие: случайные величины 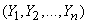 приняли совокупность значений
приняли совокупность значений 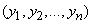 . Поставим задачу: так подобрать математические ожидания
. Поставим задачу: так подобрать математические ожидания 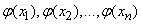 , чтобы вероятность этого события была максимальна.
, чтобы вероятность этого события была максимальна.
Строго говоря, вероятность любого из событий 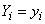 , так же как и их совмещения, равна нулю, так как величины
, так же как и их совмещения, равна нулю, так как величины 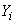 непрерывны; поэтому мы будем пользоваться не вероятностями событий
непрерывны; поэтому мы будем пользоваться не вероятностями событий 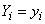 , а соответствующими элементами вероятностей:
, а соответствующими элементами вероятностей:
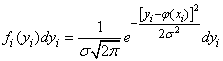 . (14.8.3)
. (14.8.3)
Найдем вероятность того, что система случайных величин 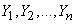 примет совокупность значений, лежащих в пределах
примет совокупность значений, лежащих в пределах
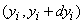
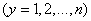 .
.
Так как опыты независимы, эта вероятность равна произведению элементов вероятностей (14.8.3) для всех значений 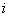 :
:
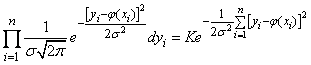 (14.8.4)
(14.8.4)
где 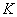 - некоторый коэффициент, не зависящий от
- некоторый коэффициент, не зависящий от 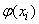 .
.
Требуется так выбрать математические ожидания 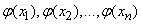 , чтобы выражение (14.8.4) обращалось в максимум.
, чтобы выражение (14.8.4) обращалось в максимум.
Величина
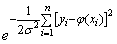
всегда меньше единицы; очевидно, она имеет наибольшее значение, когда показатель степени по абсолютной величине минимален:
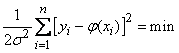 .
.
Отсюда, отбрасывая постоянный множитель 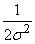 , получаем требование метода наименьших квадратов: для того чтобы данная совокупность наблюденных значений
, получаем требование метода наименьших квадратов: для того чтобы данная совокупность наблюденных значений
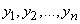
была наивероятнейшей, нужно выбрать функцию 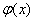 так, чтобы сумма квадратов отклонений наблюденных значений
так, чтобы сумма квадратов отклонений наблюденных значений 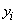 от
от 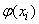 была минимальной:
была минимальной:
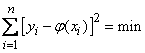 .
.
Таким образом обосновывается метод наименьших квадратов, исходя из нормального закона ошибок измерения и требования максимальной вероятности данной совокупности ошибок.
Перейдем к задаче определения параметров 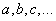 , исходя из принципа наименьших квадратов. Пусть имеется таблица экспериментальных данных (табл. 14.8.1) и пусть из каких-то соображений (связанных с существом явления или просто с внешним видом наблюденной зависимости) выбран общий вид функции
, исходя из принципа наименьших квадратов. Пусть имеется таблица экспериментальных данных (табл. 14.8.1) и пусть из каких-то соображений (связанных с существом явления или просто с внешним видом наблюденной зависимости) выбран общий вид функции 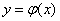 , зависящей от нескольких числовых параметров
, зависящей от нескольких числовых параметров 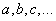 ; именно эти параметры и требуется выбрать согласно методу наименьших квадратов так, чтобы сумма квадратов отклонений
; именно эти параметры и требуется выбрать согласно методу наименьших квадратов так, чтобы сумма квадратов отклонений 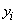 от
от 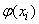 была минимальна. Запишем
была минимальна. Запишем  как функцию не только аргумента
как функцию не только аргумента  , но и параметров
, но и параметров 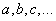 :
:
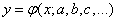 (14 8.5)
(14 8.5)
Требуется выбрать 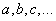 так, чтобы выполнялось условие:
так, чтобы выполнялось условие:
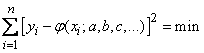 . (14.8.6)
. (14.8.6)
Найдем значения 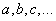 , обращающие левую часть выражения (14.8.6) в минимум. Для этого продифференцируем ее по
, обращающие левую часть выражения (14.8.6) в минимум. Для этого продифференцируем ее по 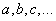 и приравняем производные нулю:
и приравняем производные нулю:
 (14.8.7)
(14.8.7)
где 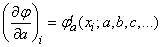 - значение частной производной функции
- значение частной производной функции 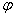 по параметру
по параметру 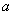 в точке
в точке 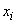 ,
, 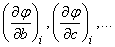 - аналогично.
- аналогично.
Система уравнений (14.8.7) содержит столько же уравнений, сколько неизвестных 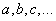 .
.
Решить систему (14.8.7) в общем виде нельзя; для этого необходимо задаться конкретным видом функции 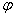 .
.
Рассмотрим два часто встречающихся на практике случая: когда функция 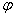 линейна и когда она выражается полиномом второй степени (параболой).
линейна и когда она выражается полиномом второй степени (параболой).
1. Об этом говорит сайт https://intellect.icu . Подбор параметров линейной функции методом наименьших квадратов
В опыте зарегистрирована совокупность значений 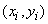
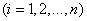 (см. рис. 14.8.6).
(см. рис. 14.8.6).

Рис. 14.8.6.
Требуется подобрать по методу наименьших квадратов параметры 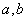 линейной функции
линейной функции
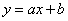 ,
,
изображающей данную экспериментальную зависимость.
Решение. Имеем:
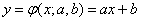 . (14.8.8)
. (14.8.8)
Дифференцируя выражение (14.8.8) по 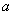 и
и 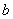 , имеем:
, имеем:
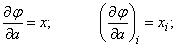
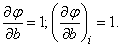
Подставляя в формулы (14.8.7), получим два уравнения для определения 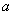 и
и 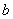 :
:
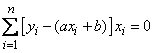 ,
,
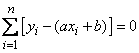 ,
,
или, раскрывая скобки и производя суммирование,
 (14.8.9)
(14.8.9)
Разделим оба уравнения (14.8.9) на 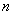 :
:
 (14.8.10)
(14.8.10)
Суммы, входящие в уравнения (14.8.10), представляют собой не что иное, как уже знакомые нам статистические моменты:
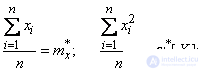

Подставляя эти выражения в систему (14.8.10), получим:
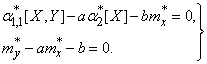 (14.8.11)
(14.8.11)
Выразим 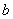 из второго уравнения (14.8.11) и подставим в первое:
из второго уравнения (14.8.11) и подставим в первое:
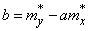 ;
;
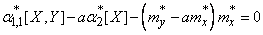 .
.
Решая последнее уравнение относительно 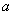 , имеем:
, имеем:
 . (14.8.12)
. (14.8.12)
Выражение (14.8.12) можно упростить, если ввести в него не начальные, а центральные моменты. Действительно,
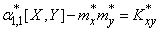 ,
, 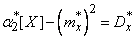 ,
,
откуда
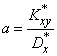 ;
; 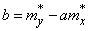 , (14.8.13)
, (14.8.13)
где
 (14.8.14)
(14.8.14)
Таким образом, поставленная задача решена, и линейная зависимость, связывающая  и
и  , имеет вид:
, имеет вид:
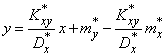 ,
,
или, перенося 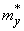 в левую часть,
в левую часть,
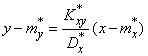 . (14.8.15)
. (14.8.15)
Мы выразили коэффициенты линейной зависимости через центральные, а не через начальные вторые моменты только потому, что в таком видe формулы имеют более компактный вид. При практическом применении выведенных формул может оказаться удобнее вычислять моменты 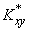 и
и 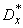 не по формулам (14.8.14), а через вторые начальные моменты:
не по формулам (14.8.14), а через вторые начальные моменты:
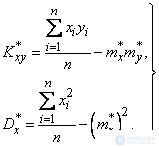 (14.8.16)
(14.8.16)
Для того чтобы формулы (14.8.16) не приводили к разностям близких чисел, рекомендуется перенести начало отсчета в точку, не слишком далекую от математических ожиданий 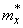 ,
, 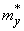 .
.
2. Подбор параметров параболы второго порядка методом наименьших квадратов
В опыте зарегистрированы значения 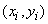
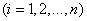 (см. рис. 14.8.7).
(см. рис. 14.8.7).
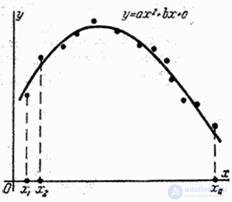
Рис. 14.8.7.
Требуется методом наименьших квадратов подобрать параметры квадратичной функции - параболы второго порядка:
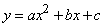 ,
,
соответствующей наблюденной экспериментальной зависимости. Имеем:
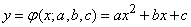 ,
,
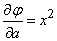 ;
; 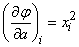 ;
;
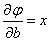 ;
; 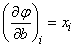 ;
;
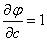 ;
; 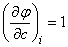 .
.
Подставляя в уравнения (14.8.7), имеем:
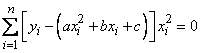 ,
,
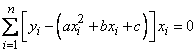 ,
,
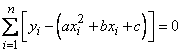
или, раскрывая скобки, производя суммирование и деля на 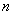 ,
,
 (14.8.17)
(14.8.17)
Коэффициенты этой системы также представляют собой статистические моменты системы двух величии 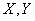 , а именно:
, а именно:
 ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  .
.
Пользуясь этими выражениями для коэффициентов через начальные моменты одной случайной величины и системы двух величин, можно придать системе уравнений (14.8.7) достаточно компактный вид. Действительно, учитывая, что 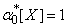 ;
; 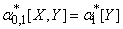 и перенося члены, не содержащие неизвестных, в правые части, приведем систему (14.8.17) к виду:
и перенося члены, не содержащие неизвестных, в правые части, приведем систему (14.8.17) к виду:
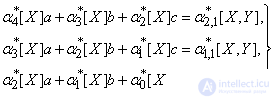 (14.8.18)
(14.8.18)
Закон образования коэффициентов в уравнениях (14.8.18) нетрудно подметить: в левой части фигурируют только моменты величины  в убывающем порядке; в правой части стоят моменты системы
в убывающем порядке; в правой части стоят моменты системы 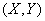 , причем порядок момента по
, причем порядок момента по  убывает от уравнения к уравнению, а порядок по
убывает от уравнения к уравнению, а порядок по 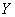 всегда остается первым.
всегда остается первым.
Аналогичными по структуре уравнениями будут определяться коэффициенты параболы любого порядка.
Мы видим, что в случае, когда экспериментальная зависимость выравнивается по методу наименьших квадратов полиномом некоторой степени, то коэффициенты этого полинома находятся решением системы линейных уравнений. Коэффициенты этой системы линейных уравнений представляют собой статистические моменты различных порядков, характеризующие систему величии 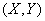 , если ее рассмотреть как систему случайных величин.
, если ее рассмотреть как систему случайных величин.
Почти так же просто решается задача сглаживания экспериментальной зависимости методом наименьших квадратов в случае, когда сглаживающая функция представляет собой не полином, а сумму произвольных заданных функций 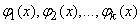 с коэффициентами
с коэффициентами 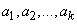 :
:
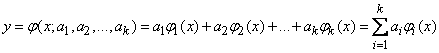 , (14.8.19)
, (14.8.19)
и когда требуется определить коэффициенты 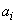 .
.
Например, экспериментальную зависимость можно сглаживать тригонометрическим полиномом
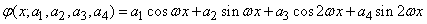
или линейной комбинацией показательных функций
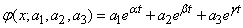 ,
,
и т. д.
В случае, если функция задается выражением типа (14.8.19), коэффициенты 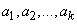 находятся решением системы
находятся решением системы 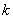 линейных уравнений вида:
линейных уравнений вида:
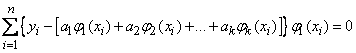 ,
,
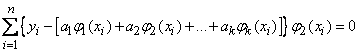 ,
,
 ,
,
 .
.
Выполняя почленное суммирование, имеем:
 ,
,
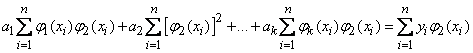 ,
,
 ,
,
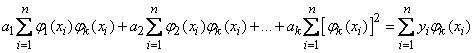 ,
,
или, короче,
 (14.8.20)
(14.8.20)
Систему линейных уравнений (14.8.20) всегда можно решить и определить таким образом коэффициенты 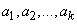 .
.
Сложнее решается задача о сглаживании методом наименьших квадратов, если в выражение функции 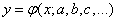 числовые параметры
числовые параметры 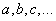 входят нелинейно. Тогда решение системы (14.8.7) может оказаться сложным и трудоемким. Однако и в этом случае часто удается получить решение задачи с помощью сравнительно простых приемов.
входят нелинейно. Тогда решение системы (14.8.7) может оказаться сложным и трудоемким. Однако и в этом случае часто удается получить решение задачи с помощью сравнительно простых приемов.
Проиллюстрируем идею, этих приемов на самом простом примере функции, нелинейно зависящей только от одного параметра 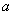 (например,
(например, 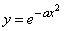 или
или 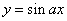 , или
, или 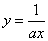 ). Имеем:
). Имеем:
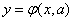 , (14.8.21)
, (14.8.21)
где 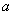 - параметр, подлежащий подбору методом наименьших квадратов для наилучшего сглаживания заданной экспериментальной зависимости (рис. 14.8.8).
- параметр, подлежащий подбору методом наименьших квадратов для наилучшего сглаживания заданной экспериментальной зависимости (рис. 14.8.8).

Рис. 14.8.8.
Будем решать задачу следующим образом. Зададимся рядом значений параметра 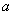 и для каждого из них найдем сумму квадратов уклонений
и для каждого из них найдем сумму квадратов уклонений 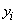 от
от 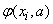 . Эта сумма квадратов есть некоторая функция
. Эта сумма квадратов есть некоторая функция 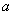 ; обозначим ее
; обозначим ее 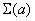 :
:
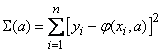 .
.
Нанесем значение 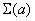 на график (рис. 14.8.9).
на график (рис. 14.8.9).
То значение 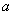 , для которого кривая
, для которого кривая 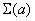 имеет минимум, и выбирается как подходящее значение параметра
имеет минимум, и выбирается как подходящее значение параметра 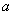 в выражении (14.8.21).
в выражении (14.8.21).
Совершенно так же, в принципе, можно, не решая уравнений (14.8.7), подобрать совокупность двух параметров 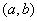 , удовлетворяющую принципу наименьших квадратов; работа при этом лишь незначительно усложнится и сведется к построению не одного, а нескольких графиков (рис. 14.8.10); при этом придется искать совокупность значений
, удовлетворяющую принципу наименьших квадратов; работа при этом лишь незначительно усложнится и сведется к построению не одного, а нескольких графиков (рис. 14.8.10); при этом придется искать совокупность значений 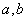 , обеспечивающую минимум минимального значения суммы квадратов отклонений
, обеспечивающую минимум минимального значения суммы квадратов отклонений 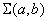 .
.
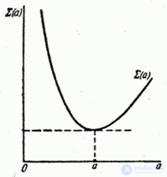
Рис. 14.8.9.
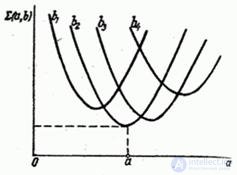
Рис. 14.8.10.
Пример1. В опыте исследована зависимость глубины проникания 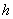 тела в преграду от удельном энергии
тела в преграду от удельном энергии 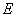 (энергии, приходящейся на квадратный сантиметр площади соударения). Экспериментальные данные приведены в таблице 14.8.2 и на графике (рис. 14.8.11).
(энергии, приходящейся на квадратный сантиметр площади соударения). Экспериментальные данные приведены в таблице 14.8.2 и на графике (рис. 14.8.11).
Таблица 14.8.2.
|
|
|
|
|
1 |
41 |
4 |
|
2 |
50 |
8 |
|
3 |
81 |
10 |
|
4 |
104 |
14 |
|
5 |
120 |
16 |
|
6 |
139 |
20 |
|
7 |
154 |
19 |
|
8 |
180 |
23 |
|
9 |
208 |
26 |
|
10 |
241 |
30 |
|
11 |
250 |
31 |
|
12 |
269 |
36 |
|
13 |
301 |
37 |
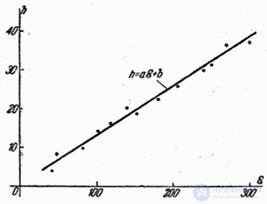
Рис. 14.8.11.
Требуется по методу наименьших квадратов подобрать и построить прямую, изображающую зависимость 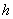 от
от 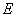 .
.
Решение. Имеем:
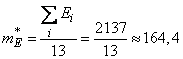 ,
, 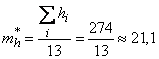 .
.
Для обработки по начальным моментам переносим начало координат в близкую к средней точку:
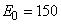 ;
; 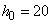 .
.
Получаем новую таблицу значений величин:
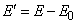 ;
; 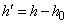
(табл. 14.8.3).
Таблица 14.8.3.
|
|
|
|
|
1 |
-109 |
-16 |
|
2 |
-100 |
-12 |
|
3 |
-69 |
-10 |
|
4 |
-46 |
-6 |
|
5 |
-30 |
-4 |
|
6 |
-11 |
0 |
|
7 |
4 |
-1 |
|
8 |
30 |
3 |
|
9 |
58 |
6 |
|
10 |
91 |
10 |
|
11 |
100 |
11 |
|
12 |
119 |
16 |
|
13 |
151 |
17 |
Определяем моменты:
 ;
;
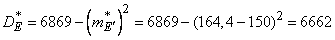 ;
;
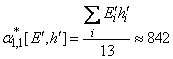 ;
;
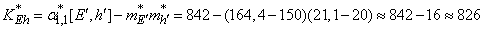 .
.
Уравнение прямой имеет вид:
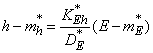 ,
,
или
 . (14.8.22)
. (14.8.22)
Прямая (14.8.22) показана на рис. 14.8.11.
Пример 2. Произведен ряд опытов по измерению перегрузки авиационной бомбы, проникающей в грунт, при различных скоростях встречи. Полученные значения перегрузки 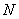 в зависимости от скорости
в зависимости от скорости 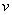 приведены в таблице 14.8.4.
приведены в таблице 14.8.4.
Таблица 14.8.4.
|
|
|
|
|
1 |
120 |
540 |
|
2 |
131 |
590 |
|
3 |
140 |
670 |
|
4 |
161 |
760 |
|
5 |
174 |
850 |
|
6 |
180 |
970 |
|
7 |
200 |
1070 |
|
8 |
214 |
1180 |
|
9 |
219 |
1270 |
|
10 |
241 |
1390 |
|
11 |
250 |
1530 |
|
12 |
268 |
1600 |
|
13 |
281 |
1780 |
|
14 |
300 |
2030 |
Построить по методу наименьших квадратов квадратичную зависимость вида:
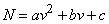 ,
,
наилучшим образом согласующуюся с экспериментальными данными.
Решение. В целях удобства обработки удобно изменить единицы измерения так, чтобы не иметь дела с многозначными числами; для этого можно значения 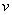 выразить в сотнях м/сек (умножить на
выразить в сотнях м/сек (умножить на 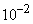 ), а
), а 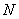 - в тысячах единиц (умножить на
- в тысячах единиц (умножить на 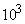 ) и всю обработку провести в этих условных единицах.
) и всю обработку провести в этих условных единицах.
Находим коэффициенты уравнений (14.8.18).
В принятых условных единицах:
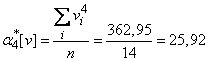 ;
;
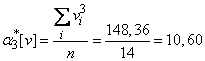 ;
;
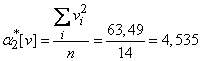 ;
;
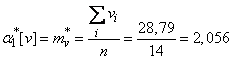 ;
;
 ;
;
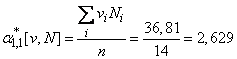 ;
;
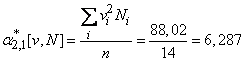 .
.
Система уравнений (14.8.18) имеет вид:
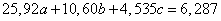 ,
,
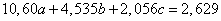 ,
,
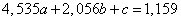 .
.
Решая эту систему, находим:
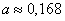 ;
; 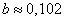 ;
; 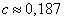 .
.
На рис. 14.8.12 нанесены экспериментальные точки и зависимость
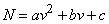 ,
,
построенная по методу наименьших квадратов.
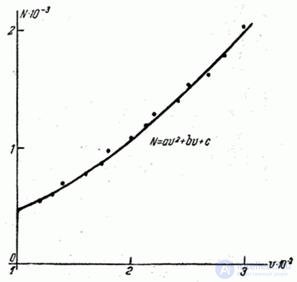
Рис. 14.8.12.
Примечание. В некоторых случаях может потребоваться провести кривую так, чтобы она точно проходила через некоторые заданные заранее точки. Тогда некоторые из числовых параметров 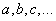 , входящих в функцию
, входящих в функцию 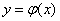 , могут быть определены из этих условий.
, могут быть определены из этих условий.
Например, в условиях примера 2 может понадобиться проэкстраполироватъ зависимость 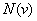 на малые значения
на малые значения 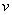 , при этом естественно провести параболу второго порядка так, чтобы она проходила через начало координат (т. е. нулевой скорости встречи соответствовала нулевая перегрузка). Тогда, естественно,
, при этом естественно провести параболу второго порядка так, чтобы она проходила через начало координат (т. е. нулевой скорости встречи соответствовала нулевая перегрузка). Тогда, естественно,  и зависимость
и зависимость 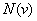 приобретает вид:
приобретает вид:
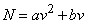 ,
,
а система уравнений для определения 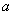 и
и 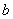 будет иметь вид:
будет иметь вид:
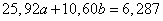 ,
,
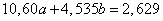 .
.
Пример 3. Конденсатор, заряженный до напряжения 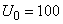 вольт, разряжается через некоторое сопротивление. Зависимость напряжения
вольт, разряжается через некоторое сопротивление. Зависимость напряжения 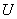 между обкладками конденсатора от времени
между обкладками конденсатора от времени 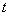 зарегистрирована на участке времени 10 сек с интервалом 1 сек. Напряжение измеряется с точностью до 5 вольт. Результаты измерений приведены в таблице 14.8.5.
зарегистрирована на участке времени 10 сек с интервалом 1 сек. Напряжение измеряется с точностью до 5 вольт. Результаты измерений приведены в таблице 14.8.5.
Таблица 14.8.5.
|
|
|
|
|
|
|
|
1 |
0 |
100 |
7 |
6 |
15 |
|
2 |
1 |
75 |
8 |
7 |
10 |
|
3 |
2 |
55 |
9 |
8 |
10 |
|
4 |
3 |
40 |
10 |
9 |
5 |
|
5 |
4 |
30 |
11 |
10 |
5 |
|
6 |
5 |
20 |
|
|
|
Согласно теоретическим данным, зависимость напряжения от времени должна иметь вид:
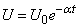 .
.
Основываясь на опытных данных, подобрать методом наименьших квадратов значение параметра 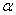 .
.
Решение. По таблицам функции 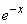 убеждаемся, что
убеждаемся, что 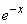 доходит приблизительно до 0,05 при
доходит приблизительно до 0,05 при 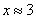 ; следовательно, коэффициент
; следовательно, коэффициент 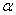 должен иметь порядок 0,3. Задаемся в районе
должен иметь порядок 0,3. Задаемся в районе 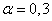 несколькими значениями
несколькими значениями 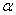 :
:
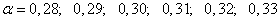
и вычисляем для них значения функции
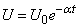
в точках 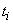 (табл. 14.8.6). В нижней строке таблицы 14.8.6 помещены значения суммы квадратов отклонений
(табл. 14.8.6). В нижней строке таблицы 14.8.6 помещены значения суммы квадратов отклонений 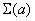 в зависимости от
в зависимости от 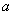 .
.
Таблица 14.8.6.
|
|
|
|
|
|
|
|
|
|
1 |
0 |
100,0 |
100,0 |
100,0 |
100,0 |
100,0 |
100,0 |
|
2 |
1 |
75,5 |
74,8 |
74,1 |
73,3 |
72,6 |
71,9 |
|
3 |
2 |
57,1 |
56,0 |
54,9 |
53,8 |
52,7 |
51,7 |
|
4 |
3 |
43,2 |
41,9 |
40,7 |
39,5 |
38,3 |
37,2 |
|
5 |
4 |
32,6 |
31,3 |
30,1 |
28,9 |
27,8 |
26,7 |
|
6 |
5 |
24,6 |
23,5 |
22,3 |
21,2 |
20,2 |
19,2 |
|
7 |
6 |
18,6 |
17,6 |
16,5 |
15,6 |
14,7 |
13,8 |
|
8 |
7 |
14,1 |
13,1 |
12,2 |
11,4 |
10,6 |
9,9 |
|
9 |
8 |
10,7 |
9,8 |
9,1 |
8,4 |
7,7 |
7,1 |
|
10 |
9 |
8,0 |
7,4 |
6,7 |
6,1 |
5,6 |
5,1 |
|
11 |
10 |
6,1 |
5,5 |
5,0 |
4,5 |
4,1 |
3,7 |
|
|
|
83,3 |
40,3 |
17,4 |
13,6 |
25,7 |
51,4 |
График функции 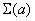 приведен на рис. 14.8.13.
приведен на рис. 14.8.13.
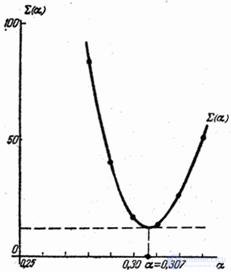
Рис. 14.8.13.
Из графика видно, что значение 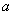 , отвечающее минимуму, приближенно равно 0,307. Таким образом, по методу наименьших квадратов наилучшим приближением к опытным данным будет функция
, отвечающее минимуму, приближенно равно 0,307. Таким образом, по методу наименьших квадратов наилучшим приближением к опытным данным будет функция  . График этой функции вместе с экспериментальными точками дан на рис. 14.8.14.
. График этой функции вместе с экспериментальными точками дан на рис. 14.8.14.
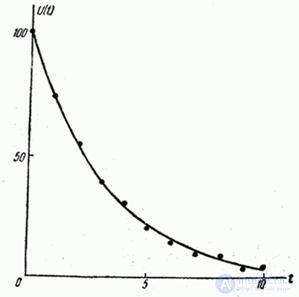
Рис. 14.8.14.
Информация, изложенная в данной статье про сглаживание экспериментальных зависимостей по методу наименьших квадратов , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое сглаживание экспериментальных зависимостей по методу наименьших квадратов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ