12.6. Композиция нормальных законов кратко

Привет, Вы узнаете о том , что такое композиция нормальных законов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое композиция нормальных законов , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Рассмотрим две независимые случайные величины 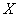 и 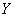, подчиненные нормальным законам:

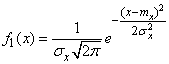,                (12.6.1)

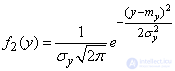 .             (12.6.2)

 

Требуется произвести композицию этих законов, т. е. найти закон распределения величины:

.

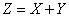Применим общую формулу (12.5.3) для композиции законов распределения:

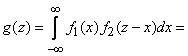
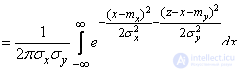.          (12.6.3)

Если раскрыть скобки в показателе степени подынтегральной функции и привести подобные члены, получим:

,

где

;

;

.

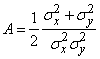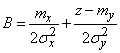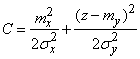Подставляя эти выражения в уже встречавшуюся нам формулу (9.1.3):

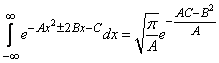,               (12.6.4)

после преобразований получим:

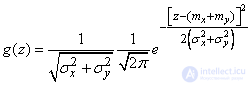,                   (12.6.5)

а это есть не что иное, как нормальный закон с центром рассеивания

            (12.6.6)

и средним квадратическим отклонением

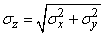.                    (12.6.7)

К тому же выводу можно прийти значительно проще с помощью следующих качественных рассуждений.

Не раскрывая скобок и не производя преобразований в подынтегральной функции (12.6.3), сразу приходим к выводу, что показатель степени есть квадратный трехчлен относительно 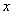 вида

,

где в коэффициент 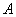 величина  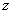не входит совсем, в коэффициент  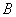входит в первой степени, а в коэффициент  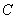- в квадрате. Об этом говорит сайт https://intellect.icu . Имея это в виду и применяя формулу (12.6.4), приходим к заключению, что  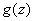есть показательная функция, показатель степени которой - квадратный трехчлен относительно 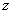, а плотность распределения такого вида соответствует нормальному закону. Таким образом, мы приходим к чисто качественному выводу: закон распределения величины  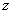должен быть нормальным.

Чтобы найти параметры этого закона - 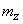 и 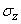 - воспользуемся теоремой сложения математических ожиданий и теоремой сложения дисперсий. По теореме сложения математических ожиданий

.                       (12.6.8)

По теореме сложения дисперсий

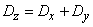
или

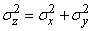,                       (12.6.9)

откуда следует формула (12.6.7).

Переходя от средних квадратических отклонений к пропорциональным им вероятным отклонениям, получим:

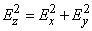.                       (12.6.10)

Таким образом, мы пришли к следующему правилу: при композиции нормальных законов получается снова нормальный закон, причем математические ожидания и дисперсии (или квадраты вероятных отклонений) суммируются.

Правило композиции нормальных законов может быть обобщено на случай произвольного числа независимых случайных величин.

Если имеется  независимых случайных величин:

,

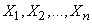подчиненных нормальным законам с центрами рассеивания

и средними квадратическими отклонениями

,

то величина

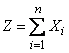
также подчинена нормальному закону с параметрами

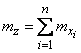,              (12.6.11)

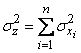.              (12.6.12)

Вместо формулы (12.6.12) можно применять равносильную ей формулу:

.              (12.6.13)

Если система случайных величин 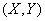 распределена по нормальному закону, но величины  зависимы, то нетрудно доказать, так же как раньше, исходя из общей формулы (12.5.1), что закон распределения величины

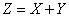
есть тоже нормальный закон. Центры рассеивания по-прежнему складываются алгебраически, но для средних квадратических отклонений правило становится более сложным:

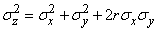,       (12.6.14)

где 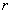 - коэффициент корреляции величин  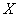и .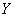

При сложении нескольких зависимых случайных величин, подчиненных в своей совокупности нормальному закону, закон распределения суммы также оказывается нормальным с параметрами

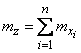,              (12.6.15)

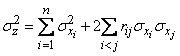,             (12.6.16)

или в вероятных отклонениях

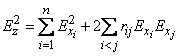,             (12.6.17)

где  - коэффициент корреляции величин , а суммирование распространяется на все различные попарные комбинации величин .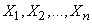

Мы убедились в весьма важном свойстве нормального закона: при композиции нормальных законов получается снова нормальный закон. Это - так называемое «свойство устойчивости». Закон распределения называется устойчивым, если при композиции двух законов этого типа получается снова закон того же типа. Выше мы показали, что нормальный закон является устойчивым. Свойством устойчивости обладают весьма немногие законы распределения. В предыдущем 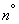 (пример 2) мы убедились, что, например, закон равномерной плотности неустойчив: при композиции двух законов равномерной плотности на участках от 0 до 1 мы получили закон Симпсона.

Устойчивость нормального закона - одно из существенных условий его широкого распространения на практике. Однако свойством устойчивости, кроме нормального, обладают и некоторые другие законы распределения. Особенностью нормального закона является то, что при композиции достаточно большого числа практически произвольных законов распределения суммарный закон оказывается сколь угодно близок к нормальному вне зависимости от того, каковы были законы распределения слагаемых. Это можно проиллюстрировать, например, составляя композицию трех законов равномерной плотности на участках от 0 до 1. Получающийся при этом закон распределения  изображен на рис. 12.6.1. Как видно из чертежа, график функции  весьма напоминает график нормального закона.

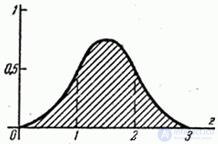
Рис. 12.6.1.

Информация, изложенная в данной статье про композиция нормальных законов , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое композиция нормальных законов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про композиция нормальных законов