Лекция
Привет, Вы узнаете о том , что такое закон пуассона, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон пуассона , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Во многих задачах практики приходится иметь дело со случайными величинами, распределенными по своеобразному закону, который называется законом Пуассона.
Рассмотрим прерывную случайную величину 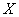 , которая может принимать только целые, неотрицательные значения:
, которая может принимать только целые, неотрицательные значения:
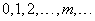 ,
,
причем последовательность этих значений теоретически не ограничена.
Говорят, что случайная величина 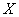 распределена по закону Пуассона, если вероятность того, что она примет определенное значение
распределена по закону Пуассона, если вероятность того, что она примет определенное значение 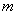 , выражается формулой
, выражается формулой
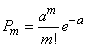
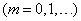 , (5.9.1)
, (5.9.1)
где а – некоторая положительная величина, называемая параметром закона Пуассона.
Ряд распределения случайной величины 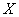 , распределенной по закону Пуассона, имеет вид:
, распределенной по закону Пуассона, имеет вид:
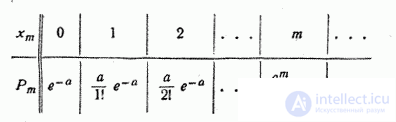
Убедимся, прежде всего, что последовательность вероятностей, задаваемая формулой (5.9.1), может представлять собой ряд распределения, т.е. что сумма всех вероятностей 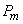 равна единице. Имеем:
равна единице. Имеем:
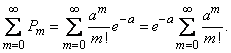
Но
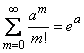 ,
,
откуда
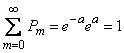 .
.
На рис. 5.9.1 показаны многоугольники распределения случайной величины 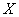 , распределенной по закону Пуассона, соответствующие различным значениям параметра
, распределенной по закону Пуассона, соответствующие различным значениям параметра 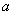 . В таблице 8 приложения приведены значения
. В таблице 8 приложения приведены значения 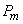 для различных
для различных 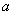 .
.
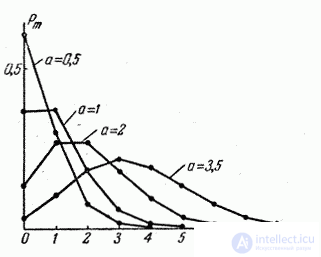
Рис. 5.9.1.
Определим основные характеристики – математическое ожидание и дисперсию – случайной величины 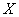 , распределенной по закону Пуассона. По определению математического ожидания
, распределенной по закону Пуассона. По определению математического ожидания
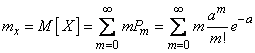 .
.
Первый член суммы (соответствующий 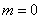 ) равен нулю, следовательно, суммирование можно начать с
) равен нулю, следовательно, суммирование можно начать с  :
:
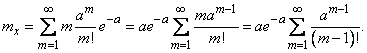
Обозначим 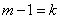 ; тогда
; тогда
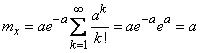 . (5.9.2)
. (5.9.2)
Таким образом, параметр 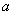 представляет собой не что иное, как математическое ожидание случайной величины
представляет собой не что иное, как математическое ожидание случайной величины 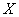 .
.
Для определения дисперсии найдем сначала второй начальный момент величины 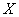 :
:
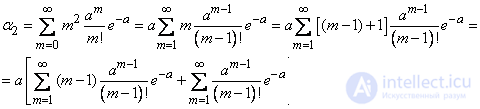
По ранее доказанному
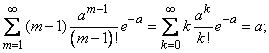
кроме того,
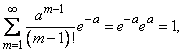
следовательно,
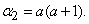
Далее находим дисперсию величины 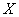 :
:
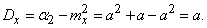 (5.9.3)
(5.9.3)
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию 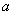 .
.
Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина 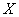 распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
Определим для случайной величины 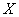 , распределенной по закону Пуассона, вероятность того, что она примет значение не меньше заданного
, распределенной по закону Пуассона, вероятность того, что она примет значение не меньше заданного 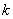 . Обозначим эту вероятность
. Обозначим эту вероятность  :
:
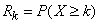 .
.
Очевидно, вероятность  может быть вычислена как сумма
может быть вычислена как сумма
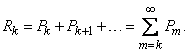
Однако значительно проще определить ее из вероятности противоположного события:
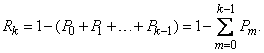 (5.9.4)
(5.9.4)
В частности, вероятность того, что величина 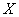 примет положительное значение, выражается формулой
примет положительное значение, выражается формулой
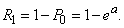 (5.9.5)
(5.9.5)
Мы уже упоминали о том, что многие задачи практики приводят к распределению Пуассона. Рассмотрим одну из типичных задач такого рода.

Рис. 5.9.2.
Пусть на оси абсцисс Ох случайным образом распределяются точки (рис. 5.9.2). Допустим, что случайное распределение точек удовлетворяет следующим условиям:
1. Вероятность попадания того или иного числа точек на отрезок 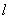 зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределяются на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность (т.е. математическое ожидание числа точек, приходящихся на единицу длины) через
зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределяются на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность (т.е. математическое ожидание числа точек, приходящихся на единицу длины) через  .
.
2. Точки распределяются на оси абсцисс независимо друг от друга, т.е. вероятность попадания того или другого числа точек на заданный отрезок не зависит от того, сколько их попало на любой другой отрезок, не перекрывающийся с ним.
3. Вероятность попадания на малый участок 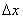 двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
Выделим на оси абсцисс определенный отрезок длины 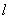 и рассмотрим дискретную случайную величину
и рассмотрим дискретную случайную величину 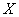 – число точек, попадающих на этот отрезок. Об этом говорит сайт https://intellect.icu . Возможные значения величины будут
– число точек, попадающих на этот отрезок. Об этом говорит сайт https://intellect.icu . Возможные значения величины будут
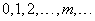 (5.9.6)
(5.9.6)
Так как точки попадают на отрезок независимо друг от друга, то теоретически не исключено, что их там окажется сколь угодно много, т.е. ряд (5.9.6) продолжается неограниченно.
Докажем, что случайная величина 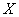 имеет закон распределения Пуассона. Для этого вычислим вероятность
имеет закон распределения Пуассона. Для этого вычислим вероятность 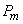 того, что на отрезок
того, что на отрезок 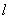 попадет ровно
попадет ровно 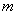 точек.
точек.
Сначала решим более простую задачу. Рассмотрим на оси Ох малый участок 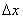 и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожидание числа точек, попадающих на этот участок, очевидно, равно
и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожидание числа точек, попадающих на этот участок, очевидно, равно 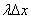 (т.к. на единицу длины попадает в среднем
(т.к. на единицу длины попадает в среднем  точек). Согласно условию 3 для малого отрезка
точек). Согласно условию 3 для малого отрезка 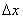 можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание
можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание 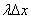 числа точек, попадающих на участок
числа точек, попадающих на участок 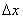 , будет приближенно равно вероятности попадания на него одной точки (или, что в наших условиях равнозначно, хотя бы одной).
, будет приближенно равно вероятности попадания на него одной точки (или, что в наших условиях равнозначно, хотя бы одной).
Таким образом, с точностью до бесконечно малых высшего порядка, при 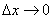 можно считать вероятность того, что на участок
можно считать вероятность того, что на участок 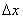 попадет одна (хотя бы одна) точка, равной
попадет одна (хотя бы одна) точка, равной 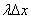 , а вероятность того, что не попадет ни одной, равной
, а вероятность того, что не попадет ни одной, равной 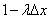 .
.
Воспользуемся этим для вычисления вероятности 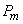 попадания на отрезок
попадания на отрезок 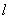 ровно
ровно 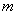 точек. Разделим отрезок
точек. Разделим отрезок 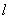 на
на 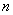 равных частей длиной
равных частей длиной 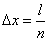 . Условимся называть элементарный отрезок
. Условимся называть элементарный отрезок 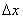 «пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно вышедоказанному вероятность того, что отрезок
«пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно вышедоказанному вероятность того, что отрезок 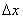 окажется «занятым», приближенно равна
окажется «занятым», приближенно равна 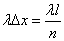 ; вероятность того, что он окажется «пустым», равна
; вероятность того, что он окажется «пустым», равна 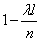 . Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n отрезков можно рассмотреть как
. Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n отрезков можно рассмотреть как 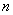 независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью
независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью 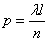 . Найдем вероятность того, что среди
. Найдем вероятность того, что среди 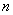 отрезков будет ровно
отрезков будет ровно 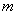 «занятых». По теореме о повторении опытов эта вероятность равна
«занятых». По теореме о повторении опытов эта вероятность равна
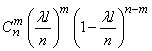
или, обозначая 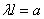 ,
,
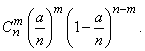 (5.9.7)
(5.9.7)
При достаточно большом 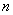 эта вероятность приближенно равна вероятности попадания на отрезок
эта вероятность приближенно равна вероятности попадания на отрезок 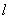 ровно
ровно 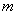 точек, так как попадание двух или больше точек на отрезок
точек, так как попадание двух или больше точек на отрезок 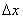 имеет пренебрежимо малую вероятность. Для того чтобы найти точное значение
имеет пренебрежимо малую вероятность. Для того чтобы найти точное значение 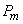 , нужно в выражении (5.9.7) перейти к пределу при
, нужно в выражении (5.9.7) перейти к пределу при 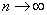 :
:
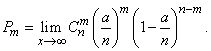 (5.9.8)
(5.9.8)
Преобразуем выражение, стоящее под знаком предела:
 (5.9.9)
(5.9.9)
Первая дробь и знаменатель последней дроби в выражении (5.9.9) при 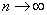 , очевидно, стремятся к единице. Выражение
, очевидно, стремятся к единице. Выражение 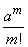 от
от 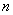 не зависит. Числитель последней дроби можно преобразовать так:
не зависит. Числитель последней дроби можно преобразовать так:
 (5.9.10)
(5.9.10)
При 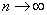
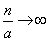 и выражение (5.9.10) стремится к
и выражение (5.9.10) стремится к 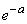 . Таким образом, доказано, что вероятность попадания ровно
. Таким образом, доказано, что вероятность попадания ровно 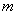 точек в отрезок
точек в отрезок 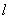 выражается формулой
выражается формулой
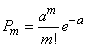 ,
,
где 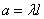 , т.е. величина Х распределена по закону Пуассона с параметром
, т.е. величина Х распределена по закону Пуассона с параметром 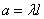 .
.
Отметим, что величина 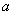 по смыслу представляет собой среднее число точек, приходящееся на отрезок
по смыслу представляет собой среднее число точек, приходящееся на отрезок 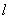 .
.
Величина 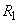 (вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок
(вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок 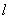 попадет хотя бы одна точка:
попадет хотя бы одна точка:
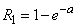 . (5.9.11)
. (5.9.11)
Таким образом, мы убедились, что распределение Пуассона возникает там, где какие-то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в какую-то область. В нашем случае такой «областью» был отрезок 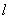 на оси абсцисс. Однако наш вывод легко распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
на оси абсцисс. Однако наш вывод легко распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
1) точки распределены в поле статистически равномерно со средней плотностью  ;
;
2) точки попадают в неперекрывающиеся области независимым образом;
3) точки появляются поодиночке, а не парами, тройками и т.д., то число точек 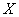 , попадающих в любую область
, попадающих в любую область  (плоскую или пространственную), распределяются по закону Пуассона:
(плоскую или пространственную), распределяются по закону Пуассона:
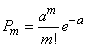
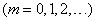 ,
,
где 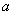 – среднее число точек, попадающих в область
– среднее число точек, попадающих в область  .
.
Для плоского случая
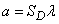 ,
,
где 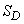 – площадь области
– площадь области  ; для пространственного
; для пространственного
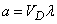 ,
,
где 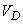 - объем области
- объем области  .
.
Заметим, что для пуассоновского распределения числа точек, попадающих в отрезок или область, условие постоянной плотности (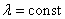 ) несущественно. Если выполнены два других условия, то
закон пуассона все равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножение плотности
) несущественно. Если выполнены два других условия, то
закон пуассона все равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножение плотности  на длину, площадь или объем области, а интегрированием переменной плотности по отрезку, площади или объему. (Подробнее об этом см. n° 19.4)
на длину, площадь или объем области, а интегрированием переменной плотности по отрезку, площади или объему. (Подробнее об этом см. n° 19.4)
Наличие случайных точек, разбросанных на линии, на плоскости или объеме – неединственное условие, при котором возникает распределение Пуассона. Можно, например, доказать, что закон Пуассона является предельным для биномиального распределения:
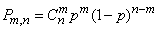 , (5.9.12)
, (5.9.12)
если одновременно устремлять число опытов 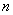 к бесконечности, а вероятность
к бесконечности, а вероятность 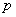 – к нулю, причем их произведение
– к нулю, причем их произведение 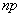 сохраняет постоянное значение:
сохраняет постоянное значение:
 . (5.9.13)
. (5.9.13)
Действительно, это предельное свойство биномиального распределения можно записать в виде:
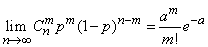 . (5.9.14)
. (5.9.14)
Но из условия (5.9.13) следует, что
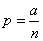 . (5.9.15)
. (5.9.15)
Подставляя (5.9.15) в (5.9.14), получим равенство
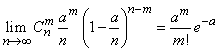 , (5.9.16)
, (5.9.16)
которое только что было доказано нами по другому поводу.
Это предельное свойство биномиального закона часто находит применение на практике. Допустим, что производится большое количество независимых опытов 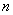 , в каждом из которых событие
, в каждом из которых событие  имеет очень малую вероятность
имеет очень малую вероятность 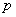 . Тогда для вычисления вероятности
. Тогда для вычисления вероятности 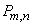 того, что событие
того, что событие  появится ровно
появится ровно 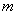 раз, можно воспользоваться приближенной формулой:
раз, можно воспользоваться приближенной формулой:
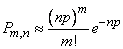 , (5.9.17)
, (5.9.17)
где  - параметр того закона Пуассона, которым приближенно заменяется биномиальное распределение.
- параметр того закона Пуассона, которым приближенно заменяется биномиальное распределение.
От этого свойства закона Пуассона – выражать биномиальное распределение при большом числе опытов и малой вероятности события – происходит его название, часто применяемое в учебниках статистики: закон редких явлений.
Рассмотрим несколько примеров, связанных с пуассоновским распределением, из различных областей практики.
Пример 1. На автоматическую телефонную станцию поступают вызовы со средней плотностью 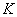 вызовов в час. Считая, что число вызовов на любом участке времени распределено по закону Пуассона, найти вероятность того, что за две минуты на станцию поступит ровно три вызова.
вызовов в час. Считая, что число вызовов на любом участке времени распределено по закону Пуассона, найти вероятность того, что за две минуты на станцию поступит ровно три вызова.
Решение. Среднее число вызовов за две минуты равно:
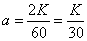 .
.
По формуле (5.9.1) вероятность поступления ровно трех вызовов равна:
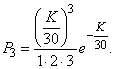
Пример 2. В условиях предыдущего примера найти вероятность того, что за две минуты придет хотя бы один вызов.
Решение. По формуле (5.9.4) имеем:
 .
.
Пример 3. В тех же условиях найти вероятность того, что за две минуты придет не менее трех вызовов.
Решение. По формуле (5.9.4) имеем:
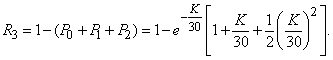
Пример 4. На ткацком станке нить обрывается в среднем 0,375 раза в течение часа работы станка. Найти вероятность того, что за смену (8 часов) число обрывов нити будет заключено в границах 2 и 4 (не менее 2 и не более 4 обрывов).
Решение. Очевидно,
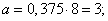
имеем:
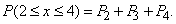
По таблице 8 приложения при 
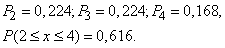
Пример 5. С накаленного катода за единицу времени вылетает в среднем  электронов, где
электронов, где 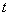 – время, протекшее с начала опыта. Найти вероятность того, что за промежуток времени длительности
– время, протекшее с начала опыта. Найти вероятность того, что за промежуток времени длительности 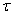 , начинающийся в момент
, начинающийся в момент 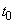 , с катода вылетит ровно m электронов.
, с катода вылетит ровно m электронов.
Решение. Находим среднее число электронов а, вылетающих с катода за данный отрезок времени. Имеем:
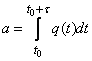 .
.
По вычисленному 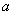 определяем искомую вероятность:
определяем искомую вероятность:
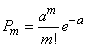 .
.
Пример 6. Число осколков, попадающих в малоразмерную цель при заданном положении точки разрыва, распределяется по закону Пуассона. Средняя плотность осколочного поля, в котором оказывается цель при данном положении точки разрыва, равна 3 оск./кв.м. Площадь цели равна  кв.м. Для поражения цели достаточно попадания в нее хотя бы одного осколка. Найти вероятность поражения цели при данном положении точки разрыва.
кв.м. Для поражения цели достаточно попадания в нее хотя бы одного осколка. Найти вероятность поражения цели при данном положении точки разрыва.
Решение. 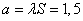 . По формуле (5.9.4) находим вероятность попадания хотя бы одного осколка:
. По формуле (5.9.4) находим вероятность попадания хотя бы одного осколка:
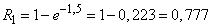 .
.
(Для вычисления значения показательной функции 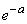 пользуемся таблицей 2 приложения).
пользуемся таблицей 2 приложения).
Пример 7. Средняя плотность болезнетворных микробов в одном кубическом метре воздуха равна 100. Берется на пробу 2 куб. дм воздуха. Найти вероятность того, что в нем будет обнаружен хотя бы один микроб.
Решение. Принимая гипотезу о пуассоновском распределении числа микробов в объеме, находим:
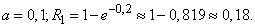
Пример 8. По некоторой цели производится 50 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,04. Пользуясь предельным свойством биномиального распределения (формула (5.9.17)), найти приближенно вероятность того, что в цель попадет: ни одного снаряда, один снаряд, два снаряда.
Решение. Имеем  . По таблице 8 приложения находим вероятности:
. По таблице 8 приложения находим вероятности:

Информация, изложенная в данной статье про закон пуассона , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое закон пуассона и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ