Лекция
Привет, Вы узнаете о том , что такое оценка вероятности по частоте, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое оценка вероятности по частоте , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
На практике часто приходится оценивать неизвестную вероятность  события
события 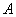 по его частоте
по его частоте  в
в  независимых опытах.
независимых опытах.
Эта задача близко примыкает к рассмотренным в предыдущих  . Действительно, частота события
. Действительно, частота события 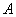 в
в  независимых опытах есть не что иное, как среднее арифметическое наблюденных значений величины
независимых опытах есть не что иное, как среднее арифметическое наблюденных значений величины  , которая в каждом отдельном опыте принимает значение 1, если событие
, которая в каждом отдельном опыте принимает значение 1, если событие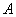 появилось, и 0, если не появилось:
появилось, и 0, если не появилось:
 . (14.5.1)
. (14.5.1)
Напомним, что математическое ожидание величины  равно
равно  ; ее дисперсия
; ее дисперсия  , где
, где  . Математическое ожидание среднего арифметического также равно
. Математическое ожидание среднего арифметического также равно 
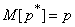 , (14.5.2)
, (14.5.2)
т. е. оценка  для
для  является несмещенной.
является несмещенной.
Дисперсия величины  равна
равна
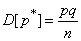 . (14.5.3)
. (14.5.3)
Можно доказать, что эта дисперсия является минимально возможной, т. е. оценка  для
для  является эффективной.
является эффективной.
Таким образом, в качестве точечной оценки для неизвестной вероятности  разумно во всех случаях принимать частоту
разумно во всех случаях принимать частоту  . Возникает вопрос о точности и надежности такой оценки, т. е. о построении доверительного интервала для вероятности
. Возникает вопрос о точности и надежности такой оценки, т. е. о построении доверительного интервала для вероятности  .
.
Хотя эта задача и представляет собой частный случай ранее рассмотренной задачи о доверительном интервале для математического ожидания, все же целесообразно решать ее отдельно. Специфика здесь в том, что величина  - прерывная случайная величина только с двумя возможными значениями: 0 и 1. Кроме того, ее математическое ожидание
- прерывная случайная величина только с двумя возможными значениями: 0 и 1. Кроме того, ее математическое ожидание  и дисперсия
и дисперсия 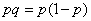 связаны функциональной зависимостью. Это упрощает задачу построения доверительного интервала.
связаны функциональной зависимостью. Это упрощает задачу построения доверительного интервала.
Рассмотрим сначала наиболее простой случай, когда число опытов  сравнительно велико, а вероятность
сравнительно велико, а вероятность  не слишком велика и не слишком мала. Тогда можно считать, что частота события
не слишком велика и не слишком мала. Тогда можно считать, что частота события  есть случайная величина, распределение которой близко к нормальному. Расчеты показывают, что этим допущением можно пользоваться даже при не очень больших значениях
есть случайная величина, распределение которой близко к нормальному. Расчеты показывают, что этим допущением можно пользоваться даже при не очень больших значениях  : достаточно, чтобы обе величины
: достаточно, чтобы обе величины 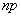 и
и  были больше четырех. Будем исходить из того, что эти условия выполнены и частоту
были больше четырех. Будем исходить из того, что эти условия выполнены и частоту  можно считать распределенной по нормальному закону. Параметрами этого закона будут:
можно считать распределенной по нормальному закону. Параметрами этого закона будут:
 ;
;  . (14.5.4)
. (14.5.4)
Предположим сначала, что величина  нам известна. Назначим доверительную вероятность
нам известна. Назначим доверительную вероятность 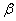 и найдем такой интервал
и найдем такой интервал  ,чтобы величина
,чтобы величина  попадала в этот интервал с вероятностью
попадала в этот интервал с вероятностью 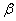 :
:
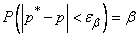 . (14.5.5)
. (14.5.5)
Так как величина  распределена нормально, то
распределена нормально, то
 ,
,
откуда, как и в 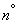 14.3,
14.3,
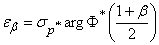 ,
,
где  - функция, обратная нормальной функции распределения
- функция, обратная нормальной функции распределения  .
.
Для определения 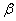 , как и в
, как и в 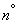 14,3, можно обозначить
14,3, можно обозначить
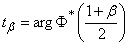 .
.
Тогда
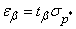 , (14.5.6)
, (14.5.6)
где  определяется из таблицы 14.3.1.
определяется из таблицы 14.3.1.
Таким образом, с вероятностью 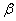 можно утверждать, что
можно утверждать, что
 . (14.5.7)
. (14.5.7)
Фактически величина  нам неизвестна; однако неравенство (14.5.7) будет иметь вероятность
нам неизвестна; однако неравенство (14.5.7) будет иметь вероятность 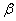 независимо от того, известна нам или неизвестна вероятность
независимо от того, известна нам или неизвестна вероятность  . Получив из опыта конкретное значение частоты
. Получив из опыта конкретное значение частоты  , можно, пользуясь неравенством (14.5.7), найти интервал
, можно, пользуясь неравенством (14.5.7), найти интервал 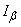 , который с вероятностью
, который с вероятностью 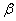 накрывает точку
накрывает точку  . Действительно, преобразуем это неравенство к виду
. Действительно, преобразуем это неравенство к виду
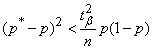 (14.5.8)
(14.5.8)
и дадим ему геометрическую интерпретацию. Будем откладывать по оси абсцисс частоту  , а по оси ординат - вероятность
, а по оси ординат - вероятность  (рис. 14.5.1).
(рис. 14.5.1).
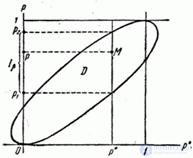
Рис. 14.5.1.
Геометрическим местом точек, координаты которых  и
и  удовлетворяют неравенству (14.5.8), будет внутренняя часть эллипса, проходящего через точки
удовлетворяют неравенству (14.5.8), будет внутренняя часть эллипса, проходящего через точки 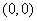 и
и 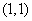 и имеющего в этих точках касательные, параллельные оси
и имеющего в этих точках касательные, параллельные оси  . Так как величина
. Так как величина  не может быть ни отрицательной, ни большей единицы, то область
не может быть ни отрицательной, ни большей единицы, то область  , соответствующую неравенству (14.5.8), нужно еще ограничить слева и справа прямыми
, соответствующую неравенству (14.5.8), нужно еще ограничить слева и справа прямыми  и
и  . Теперь можно для любого значения
. Теперь можно для любого значения  , полученного из опыта, построить доверительный интервал
, полученного из опыта, построить доверительный интервал 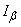 , который с вероятностью
, который с вероятностью 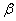 накроет неизвестное значение
накроет неизвестное значение  . Для этого проведем через точку
. Для этого проведем через точку  прямую, параллельную оси ординат; на этой прямой границы области
прямую, параллельную оси ординат; на этой прямой границы области  отсекут доверительный интервал
отсекут доверительный интервал 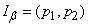 . Об этом говорит сайт https://intellect.icu . Действительно, точка
. Об этом говорит сайт https://intellect.icu . Действительно, точка  со случайной абсциссой
со случайной абсциссой  и неслучайной (но неизвестной) ординатой
и неслучайной (но неизвестной) ординатой  с вероятностью
с вероятностью 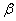 попадет внутрь эллипса, т. е. интервал
попадет внутрь эллипса, т. е. интервал 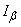 с вероятностью
с вероятностью 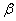 накроет точку
накроет точку  .
.
Размеры и конфигурация «доверительного эллипса» зависят от числа опытов  . Чем больше
. Чем больше  , тем больше вытянут эллипс и тем уже доверительный интервал.
, тем больше вытянут эллипс и тем уже доверительный интервал.
Доверительные границы  и
и 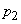 можно найти из соотношения (14.5.8), заменив в нем знак неравенства равенством. Решая полученное квадратное уравнение относительно
можно найти из соотношения (14.5.8), заменив в нем знак неравенства равенством. Решая полученное квадратное уравнение относительно  , получим два корня:
, получим два корня:
 (14.5.9)
(14.5.9)
Доверительный интервал для вероятности  будет
будет
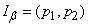 .
.
Пример 1. Частота события 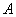 в серии из 100 опытов оказалась
в серии из 100 опытов оказалась  . Определить 90%-й доверительный интервал для вероятности
. Определить 90%-й доверительный интервал для вероятности  события
события 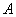 .
.
Решение. Прежде всего проверяем применимость нормального закона; для этого оценим величины 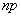 и
и  . Полагая ориентировочно
. Полагая ориентировочно  , получим
, получим
 ;
; 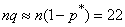 .
.
Обе величины значительно больше четырех; нормальный закон применим. Из таблицы 14.3.1 для 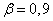 находим
находим 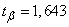 . По формулам (14.5.9) имеем
. По формулам (14.5.9) имеем
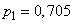 ;
; 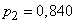 ;
;  .
.
Заметим, что при увеличении  величины
величины 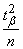 и
и  в формулах (14.5.9) стремятся к нулю; в пределе формулы принимают вид
в формулах (14.5.9) стремятся к нулю; в пределе формулы принимают вид
 (14.5.10)
(14.5.10)
Эти формулы могут быть получены и непосредственно, если воспользоваться приближенным способом построения доверительного интервала для математического ожидания, данным в 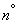 14.3. Формулами (14.5.10) можно пользоваться при больших
14.3. Формулами (14.5.10) можно пользоваться при больших  (порядка сотен), если только вероятность
(порядка сотен), если только вероятность  не слишком велика и не слишком мала (например, когда обе величины
не слишком велика и не слишком мала (например, когда обе величины 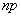 и
и  порядка 10 или более).
порядка 10 или более).
Пример 2. Произведено 200 опытов; частота события 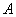 оказалась
оказалась 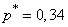 . Построить 85%-й доверительный интервал для вероятности события приближенно (по формулам (14.5.10)). Сравнить результат с точным, соответствующим формулам (14.5.9).
. Построить 85%-й доверительный интервал для вероятности события приближенно (по формулам (14.5.10)). Сравнить результат с точным, соответствующим формулам (14.5.9).
Решение.  ; по таблице 14.3.1 находим
; по таблице 14.3.1 находим  . Умножая его на
. Умножая его на
 ,
,
получим
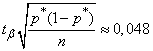 ,
,
откуда находим приближенно доверительный интервал
 .
.
По формулам (14.5.9) найдем более точные значения 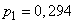 ;
; 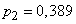 , которые почти не отличаются от приближенных.
, которые почти не отличаются от приближенных.
Выше мы рассмотрели вопрос о построении доверительного интервала для случая достаточно большого числа опытов, когда частоту можно считать распределенной нормально. При малом числе опытов (а также если вероятность  очень велика или очень мала) таким допущением пользоваться нельзя. В этом случае доверительный интервал строят, исходя не из приближенного, а из точного закона распределения частоты. Нетрудно убедиться, что это есть биномиальное распределение, рассмотренное в главах 3 и 4. Действительно, число появлений события
очень велика или очень мала) таким допущением пользоваться нельзя. В этом случае доверительный интервал строят, исходя не из приближенного, а из точного закона распределения частоты. Нетрудно убедиться, что это есть биномиальное распределение, рассмотренное в главах 3 и 4. Действительно, число появлений события 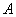 в
в  опытах распределено по биномиальному закону: вероятность того, что событие
опытах распределено по биномиальному закону: вероятность того, что событие 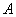 появится ровно
появится ровно 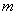 раз, равна
раз, равна
 , (14.5.11)
, (14.5.11)
а частота  есть не что иное, как число появлений события, деленное на число опытов.
есть не что иное, как число появлений события, деленное на число опытов.
Исходя из этого распределения, можно построить доверительный интервал 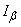 аналогично тому, как мы строили его, исходя из нормального закона для больших
аналогично тому, как мы строили его, исходя из нормального закона для больших  (стр. 331).
(стр. 331).
Предположим сначала, что вероятность  нам известна, и найдем интервал частот
нам известна, и найдем интервал частот 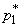 ,
, 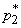 , в который с вероятностью
, в который с вероятностью 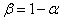 попадет частота события
попадет частота события  .
.
Для случая большого  мы пользовались нормальным законом распределения и брали интервал симметричным относительно математического ожидания. Биномиальное распределение (14.5.11) не обладает симметрией. К тому же (в связи с тем, что частота - прерывная случайная величина) интервала, вероятность попадания в который в точности равна
мы пользовались нормальным законом распределения и брали интервал симметричным относительно математического ожидания. Биномиальное распределение (14.5.11) не обладает симметрией. К тому же (в связи с тем, что частота - прерывная случайная величина) интервала, вероятность попадания в который в точности равна 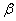 , может и не существовать. Поэтому выберем в качестве интервала
, может и не существовать. Поэтому выберем в качестве интервала 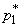 ,
, 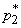 самый малый интервал, вероятность попадания левее которого и правее которого будет больше
самый малый интервал, вероятность попадания левее которого и правее которого будет больше 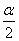 .
.
Аналогично тому, как мы строили область  для нормального закона (рис. 14.5.1), можно будет для каждого
для нормального закона (рис. 14.5.1), можно будет для каждого  и заданного
и заданного 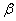 построить область, внутри которой значение вероятности
построить область, внутри которой значение вероятности  совместимо с наблюденным в опыте значением частоты р*.
совместимо с наблюденным в опыте значением частоты р*.
На рис. 14.5.2 изображены кривые, ограничивающие такие области для различных  при доверительной вероятности
при доверительной вероятности 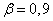 . По оси абсцисс откладывается частота
. По оси абсцисс откладывается частота  , по оси ординат - вероятность
, по оси ординат - вероятность  . Каждая пара кривых, соответствующая данному
. Каждая пара кривых, соответствующая данному  , определяет доверительный интервал вероятностей, отвечающий данному значению частоты. Строго говоря, границы областей должны быть ступенчатыми (ввиду прерывности частоты), но для удобства они изображены в виде плавных кривых.
, определяет доверительный интервал вероятностей, отвечающий данному значению частоты. Строго говоря, границы областей должны быть ступенчатыми (ввиду прерывности частоты), но для удобства они изображены в виде плавных кривых.
Для того чтобы, пользуясь такими кривыми, найти доверительный интервал 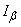 нужно произвести следующее построение (см. рис. 14.5.2): по оси абсцисс отложить наблюденное в опыте значение частоты
нужно произвести следующее построение (см. рис. 14.5.2): по оси абсцисс отложить наблюденное в опыте значение частоты  , провести через эту точку прямую, параллельную оси ординат, и отметить точки пересечения прямой с парой кривых, соответствующих данному числу опытов
, провести через эту точку прямую, параллельную оси ординат, и отметить точки пересечения прямой с парой кривых, соответствующих данному числу опытов  ; проекции этих точек на ось ординат и дадут границы
; проекции этих точек на ось ординат и дадут границы  ,
, 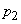 доверительного интервала
доверительного интервала 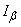

Рис. 14.5.2.
При заданном  кривые, ограничивающие «доверительную область», определяются уравнениями:
кривые, ограничивающие «доверительную область», определяются уравнениями:
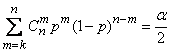 ; (14.5.12)
; (14.5.12)
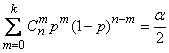 (14.5.13)
(14.5.13)
где  - число появлений события:
- число появлений события:
 .
.
Разрешая уравнение (14.5.12) относительно  , можно найти нижнюю границу
, можно найти нижнюю границу  «доверительной области»; аналогично из (14.5.13) можно найти
«доверительной области»; аналогично из (14.5.13) можно найти 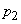 .
.
Чтобы не решать эти уравнения каждый раз заново, удобно заранее затабулировать (или представить графически) решения для нескольких типичных значений доверительной вероятности 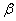 . Например, в книге И. В. Дунина-Барковского и Н. В. Смирнова «Теория вероятностей и математическая статистика в технике» имеются таблицы
. Например, в книге И. В. Дунина-Барковского и Н. В. Смирнова «Теория вероятностей и математическая статистика в технике» имеются таблицы  и
и 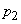 для
для  и
и  . Из той же книги заимствован график рис. 14.5.2.
. Из той же книги заимствован график рис. 14.5.2.
Пример 3. Найти доверительные границы  и
и 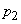 для вероятности события, если в 50 опытах частота его оказалась
для вероятности события, если в 50 опытах частота его оказалась  . Доверительная вероятность
. Доверительная вероятность 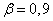 .
.
Решение. Построением (см. пунктир на рис. 14.5.2) для  и
и 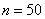 находим:
находим: 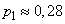 ;
;  .
.
Пользуясь методом доверительных интервалов, можно приближенно решить и другой важный для практики вопрос: каково должно быть число опытов  для того, чтобы с доверительной вероятностью 3 ожидать, что ошибка от замены вероятности частотой не превзойдет заданного значения?
для того, чтобы с доверительной вероятностью 3 ожидать, что ошибка от замены вероятности частотой не превзойдет заданного значения?
При решении подобных задач удобнее не пользоваться непосредственно графиками типа рис. 14.5.2, а перестроить их, представив доверительные границы как функции от числа опытов  .
.
Пример 4. Проведено 25 опытов, в которых событие 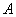 произошло 12 раз. Найти ориентировочно число опытов
произошло 12 раз. Найти ориентировочно число опытов  , которое понадобится для того, чтобы с вероятностью
, которое понадобится для того, чтобы с вероятностью 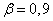 ошибка от замены вероятности частотой не превзошла 20%.
ошибка от замены вероятности частотой не превзошла 20%.
Решение. Определяем предельно допустимую ошибку:
 .
.
Пользуясь кривыми рис. 14.5.2, построим новый график: по оси абсцисс отложим число опытов  , по оси ординат - доверительные границы для вероятности (рис. 14.5.3).
, по оси ординат - доверительные границы для вероятности (рис. 14.5.3).
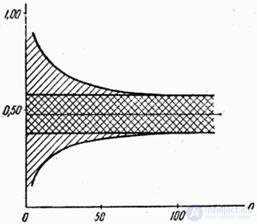
Рис. 14.5.3.
Средняя прямая, параллельная оси абсцисс, соответствует наблюденной частоте события  . Выше и ниже прямой
. Выше и ниже прямой 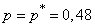 проведены кривые
проведены кривые  и
и  , изображающие нижнюю и верхнюю доверительные границы в зависимости от
, изображающие нижнюю и верхнюю доверительные границы в зависимости от  . Область между кривыми, определяющая доверительный интервал, заштрихована. В непосредственной близости от прямой
. Область между кривыми, определяющая доверительный интервал, заштрихована. В непосредственной близости от прямой 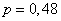 двойной штриховкой показана более узкая область 20%-й допустимой ошибки. Из рис. 14.5.3 видно, что ошибка падает до допустимой величины при числе опытов
двойной штриховкой показана более узкая область 20%-й допустимой ошибки. Из рис. 14.5.3 видно, что ошибка падает до допустимой величины при числе опытов  порядка 100.
порядка 100.
Заметим, что после выполнения потребного числа опытов может понадобиться новая проверка точности определения вероятности по частоте, так как будет получено в общем случае уже другое значение частоты отличное от наблюденного в ранее проведенных опытах. При этом может оказаться, что число опытов все еще недостаточно для обеспечения необходимой точности, и его придется несколько увеличить. Однако первое приближение, полученное описанным выше методом, может служить для ориентировочного предварительного планирования серии опытов с точки зрения требуемого на них времени, денежных затрат и т. д.
На практике иногда приходится встречаться со своеобразной задачей определения доверительного интервала для вероятности события, когда полученная из опыта частота равна нулю. Такая задача обычно связана с опытами, в которых вероятность интересующего нас события очень мала (или, наоборот, очень велика - тогда мала вероятность противоположного события).
Пусть, например, проводятся испытания какого-то изделия на безотказность работы. В результате испытаний изделие не отказало ни разу. Требуется найти максимальную практически возможную вероятность отказа.
Поставим эту задачу в общем виде. Произведено  независимых опытов, ни в одном из которых событие
независимых опытов, ни в одном из которых событие 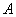 не произошло. Задана доверительная вероятность
не произошло. Задана доверительная вероятность 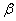 ; требуется построить доверительный интервал для вероятности
; требуется построить доверительный интервал для вероятности  события
события 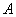 , точнее - найти его верхнюю границу
, точнее - найти его верхнюю границу 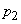 так как нижняя
так как нижняя  , естественно, равна нулю.
, естественно, равна нулю.
Поставленная задача является частным случаем общей задачи о доверительном интервале для вероятности, но ввиду своих особенностей заслуживает отдельного рассмотрения. Прежде всего, приближенный метод построения доверительного интервала (на основе замены закона распределения частоты нормальным), изложенный в начале данного 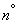 , здесь неприменим, так как вероятность
, здесь неприменим, так как вероятность  очень мала. Точный метод построения доверительного интервала на основе биномиального распределения в данном случае применим, но может быть существенно упрощен.
очень мала. Точный метод построения доверительного интервала на основе биномиального распределения в данном случае применим, но может быть существенно упрощен.
Будем рассуждать следующим образом. В результате  опытов наблюдено событие
опытов наблюдено событие  , состоящее в том, что
, состоящее в том, что 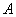 не появилось ни разу. Требуется найти максимальное значение
не появилось ни разу. Требуется найти максимальное значение  , которое «совместимо» с наблюденным в опыте событием
, которое «совместимо» с наблюденным в опыте событием  , если считать «несовместимыми» с
, если считать «несовместимыми» с  те значения
те значения  , для которых вероятность события
, для которых вероятность события  меньше, чем
меньше, чем  .
.
Очевидно, для любой вероятности  события
события 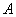 вероятность наблюденного события
вероятность наблюденного события  равна
равна
 .
.
Полагая 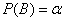 , получим уравнение для
, получим уравнение для 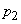 :
:
 , (14.5.14)
, (14.5.14)
откуда
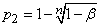 . (14.5.15)
. (14.5.15)
Пример 5. Вероятность  самопроизвольного срабатывания взрывателя при падении снаряда с высоты
самопроизвольного срабатывания взрывателя при падении снаряда с высоты  неизвестна, но предположительно весьма мала. Произведено 100 опытов, в каждом из которых снаряд роняли с высоты
неизвестна, но предположительно весьма мала. Произведено 100 опытов, в каждом из которых снаряд роняли с высоты  , но ни в одном опыте взрыватель не сработал. Определить верхнюю границу
, но ни в одном опыте взрыватель не сработал. Определить верхнюю границу 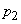 90%-го доверительного интервала для вероятности
90%-го доверительного интервала для вероятности  .
.
Решение. По формуле (14.5.15)
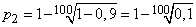 ,
,
 ;
;
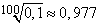 ;
;  .
.
Рассмотрим еще одну задачу, связанную с предыдущей. Событие 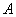 с малой вероятностью
с малой вероятностью  не наблюдалось в серии из
не наблюдалось в серии из  опытов ни разу. Задана доверительная вероятность
опытов ни разу. Задана доверительная вероятность 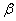 . Каково должно быть число опытов
. Каково должно быть число опытов  для того, чтобы верхняя доверительная граница для вероятности события была равна заданному значению
для того, чтобы верхняя доверительная граница для вероятности события была равна заданному значению 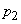 ?
?
Решение сразу получается из формулы (14.5.14):
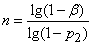 . (14.5.16)
. (14.5.16)
Пример 6. Сколько раз нужно убедиться в безотказной работе изделия для того, чтобы с гарантией 95% утверждать, что в практическом применении оно будет отказывать не более чем в 5% всех случаев?
Решение. По формуле (14.5.16) при  ,
, 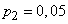 имеем:
имеем:
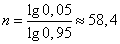 .
.
Округляя в большую сторону, получим:
 .
.
Имея в виду ориентировочный характер всех расчетов подобного рода, можно предложить вместо формул (14.5.15) и (14.5.16) более простые приближенные формулы. Их можно получить, предполагая, что число появлений события 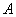 при
при  опытах распределено по закону Пуассона с математическим ожиданием
опытах распределено по закону Пуассона с математическим ожиданием  . Это предположение приближенно справедливо в случае, когда вероятность
. Это предположение приближенно справедливо в случае, когда вероятность  очень мала (см. гл. 5.
очень мала (см. гл. 5. 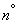 5.9). Тогда
5.9). Тогда
 ,
,
и вместо формулы (14.5.15) получим:
 , (14.5.17)
, (14.5.17)
а вместо формулы (14.5.16)
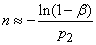 . (14.5.18)
. (14.5.18)
Пример 7. Найти приближенно значение 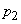 для условий примера 5.
для условий примера 5.
Решение. По формуле (14.5.14) имеем:
 ,
,
т. е. тот же результат, который получен по точной формуле в примере 5.
Пример 8. Найти приближенно значение  для условий примера 6.
для условий примера 6.
Решение. По формуле (14.5.18) имеем:
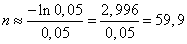 .
.
Округляя в большую сторону, находим 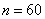 , что мало отличается от результата
, что мало отличается от результата  , полученного в примере 6.
, полученного в примере 6.
Информация, изложенная в данной статье про оценка вероятности по частоте , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое оценка вероятности по частоте и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ