Лекция
Привет, сегодня поговорим про симметрия относительно прямой, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое симметрия относительно прямой, ось симметрии , настоятельно рекомендую прочитать все из категории Планометрия.
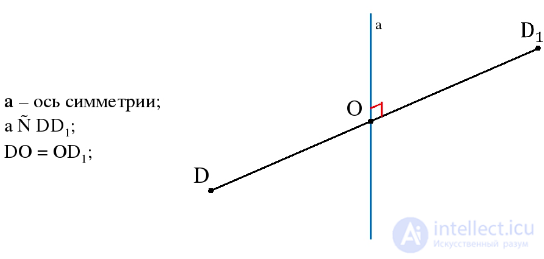
Симметрией относительно прямой или осевой симметрией относительно прямой а называется преобразование пространства, переводящее точку А в точку А1, что прямоя а - серединный перпендикуляр к отрезку АА1. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.

симметрия относительно прямой " src="/th/25/blogs/id3391/0_1.jpg" />
Есть прямая l и точка A не лежащая на прямой. Об этом говорит сайт https://intellect.icu . Опустим из точки A на прямую l перпендикуляр. На продолжении этого перпендикуляра отложим отрезок OA` = OA. Точка A` является симметричной точке A относительно прямой l.
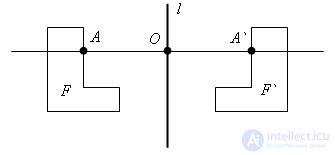
Преобразованием симметрии относительно прямой l, называется такое преобразование фигуры F в фигуру F`, при котором каждая ее точка A переходит в точку A`, симметричную относительно прямой l. Такие фигуры F и F` называются симметричными относительно прямой l. Если преобразование фигуры относительно прямой l переводит ее в саму себя, то эта фигура называется симметричной относительно данной прямой l, а прямая l называется осью симметрии фигуры.
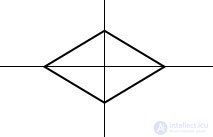
Так ромб симметричен сам себе относительно своих диагоналей. Диагонали ромба являются его осями симметрии.
Я что-то не договорил про симметрия относительно прямой, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое симметрия относительно прямой, ось симметрии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия
Из статьи мы узнали кратко, но содержательно про симметрия относительно прямой
Комментарии
Оставить комментарий
Планометрия
Термины: Планометрия