Параллелограмм. Признаки параллелограмма кратко

Привет, мой друг, тебе интересно узнать все про параллелограмм, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое параллелограмм, признаки параллелограмма , настоятельно рекомендую прочитать все из категории Планометрия.

параллелограмм ом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Параллелограммы имеют множество применений в различных областях, включая геометрию, физику, инженерное дело, компьютерную графику и другие науки. Вот некоторые области, где параллелограммы могут быть использованы:

1. Геометрия: Параллелограммы - это одна из основных фигур в геометрии, и изучение их свойств позволяет решать различные геометрические задачи и доказывать теоремы.

2. Геодезия и картография: В измерении земельных участков и составлении карт используются параллелограммы для определения углов и расстояний.

3. Архитектура и инженерное дело: Параллелограммы часто встречаются в строительстве, проектировании зданий, мостов и других инженерных конструкций.

4. Физика и механика: Параллелограммы используются для анализа сил и векторов, а также для решения задач на механику.

5. Компьютерная графика: Параллелограммы часто используются для представления и трансформации двухмерных объектов в компьютерной графике.

6. Техническое черчение: Параллелограммы применяются для построения и измерения углов в техническом черчении.

7. Статистика и экономика: В экономических и статистических исследованиях параллелограммы могут использоваться для визуализации данных и анализа трендов.

8. Кристаллография: В кристаллографии структуры кристаллических решеток могут быть представлены в виде параллелограммов.

Это только небольшой список примеров. Об этом говорит сайт https://intellect.icu . Фактически параллелограммы и их свойства широко применяются в различных областях науки, инженерии и дизайна.

Теорема.

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.



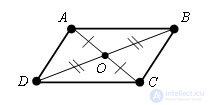
Доказательство.

Пусть ABCD – данный параллелограмм, O – точка пересечения диагоналей данного параллелограмма.
Δ AOD = Δ COB по первому признаку равенства треугольников (OD = OB, AO = OC по условию теоремы, ∠ AOD = ∠ COB, как вертикальные углы). Следовательно, ∠ OBC = ∠ ODA. А они являются внутренними накрест лежащими для прямых AD и BC и секущей BD. По признаку параллельности прямых прямые AD и BC параллельны. Так же доказываем, что AB и DC тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана.

Теорема.

Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.



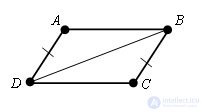
Пусть ABCD – данный четырехугольник. AD параллельно BC и AD = BC.
Тогда Δ ADB = Δ CBD по первому признаку равенства треугольников (∠ ADB = ∠ CBD, как внутренние накрест лежащие между прямыми AD и BC и секущей DB, AD=BC по условию, DB – общая).
Следовательно, ∠ ABD = ∠ CDB, а эти углы являются внутренними накрест лежащими для прямых AB и CD и секущей DB. По теореме признаке параллельности прямых AB и CD параллельны. Значит, ABCD – параллелограмм. Теорема доказана.

Теорема.

Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.



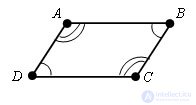
Доказательство.

Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.



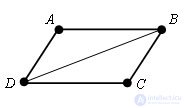
Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников ABD и BCD. Так как сумма углов в треугольнике равна 180 º,
∠ DAB + ∠ BCD + ∠ ABC + ∠ CDA.= 360 º. Так как противолежащие углы в четырехугольнике равны, то ∠ DAB + #8736 ABC = 180 º и ∠ BCD + ∠ CDA = 180 º.
Углы BCD и CDA являются внутренними односторонними для прямых AD и ВС и секущей DC, их сумма равна 180 º, поэтому из следствия к теореме о признаке параллельности прямых, прямые AD и ВС параллельны. Так же доказывается, что AB || DC. Таким образом, четырехугольник ABCD – параллелограмм по определению. Теорема доказана.

Вау!! 😲 Ты еще не читал? Это зря!

• антипараллелограмм ,
• свойство ромба ,
• свойства прямоугольника ,
• свойства параллелограмма ,
• прямоугольник , признак прямоугольника , золотой прямоугольник ,

Я что-то не договорил про параллелограмм, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое параллелограмм, признаки параллелограмма и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия

Из статьи мы узнали кратко, но содержательно про параллелограмм