Лекция
Привет, Вы узнаете о том , что такое антибиссектриса угла треугольника , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое антибиссектриса угла треугольника , антибиссектриса , настоятельно рекомендую прочитать все из категории Планометрия.
антибиссектриса угла треугольника (от лат. anti, bi- «двойное» и sectio «разрезание») — определенный луч с началом в вершине угла, делящий угол на два угла.
Антибиссектриса внутреннего угла — геометрическое место точек внутри угла, расстояния которых до двух сторон угла обратно пропорциональны квадратам этих сторон.
В треугольнике под антибиссектрисой угла может также пониматься отрезок антибиссектрисы этого угла до ее пересечения с противолежащей стороной.
Как и биссектрисы, антибиссектрисы можно провести не только к внутренним, но и к внешним углам треугольника. При этом сохраняется свойство их взаимной изотомичности или изотомической сопряженности.
Антибиссектрисы треугольника впервые введены Óканем (D’Ocagne).
Мы предполагаем известными определения изогонального чевиана и изометрического чевиана; мы напомним, что антибиссектриса, антисимедиана и антивысота являются изометриками биссектриса симедианы и высоты в треугольнике.
Также известно следующее соотношение Штейнера (1828 г.) для изогональных чевиан
и 
Теперь мы докажем, что существует аналогичное соотношение для изометрических чевианов.
Предложение
Рассмотрим в треугольнике ABC Пусть и два изометрических чевиана, то существует следующее соотношение:
Доказательство
рисунок 1
Из теоремы о синусе, примененной к треугольникам ABA1, ACA1, следует (см. Об этом говорит сайт https://intellect.icu . Рисунок выше)
Из соотношений (1) и (2) сохраняем
Теорема синуса применяется в треугольниках 
приводит к
Из соотношений (4) и (5) получаем:
Потому что 
и 
чевианы изометричны из соотношений (3) и (6) мы получаем соотношение (*) из формулировки предложения.
Приложения
1. Если AA1 - биссектриса в треугольнике ABC и 
его изометричный, то есть антибиссектриса, то из (*) получаем
Учитывая теорему о синусе в треугольнике ABC, получаем
2. Если 
симедиана и 
- антисимедиана, из (*) получаем
Действительно, будучи симмедианной, является изогональной медианы AM и
3. Если - высота в треугольнике ABC, 
и - его изометрия (антивысота), соотношение (*) становится.
На самом деле
следовательно
Из (*) получается
или
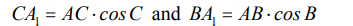
следовательно
4. Если 
- изогональ антибиссектрисы 
тогда
(Морис Д’Окань, 1883)
Доказательство
Соотношение Штейнера для 
и 
- это
Но 
- биссектриса и согласно теореме о биссектрисе 
но 
и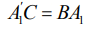 
поэтому
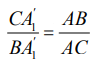
и получаем соотношение Д’Оканя
5. Если в треугольнике ABC чевиан 
изогональна симедиане 
тогда
Доказательство
Поскольку AA1 - симедиана, из отношения Штейнера мы выводим, что
Соотношение Штейнера для 
дает нам
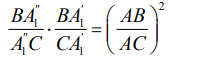
Учитывая прецедентное соотношение, получаем
6. Если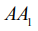 
- изогональ анти-высоты 
в треугольнике ABC, в котором высота AA1 имеет 
, тогда
Доказательство
Если AA1 высота в треугольнике ABC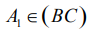 
, то
Потому что 
антимедиана, имеем 
и 
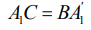тогда 
Наблюдение
Прецедентные результаты могут быть обобщены для античевианов ранга k и их изогональный.
антисиммедиана
антивысоты
Исследование, описанное в статье про антибиссектриса угла треугольника , подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое антибиссектриса угла треугольника , антибиссектриса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия
Из статьи мы узнали кратко, но содержательно про антибиссектриса угла треугольника
Комментарии