Параллельные кривые

Привет, Вы узнаете о том , что такое параллельные кривые, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое параллельные кривые, параллельная кривая , настоятельно рекомендую прочитать все из категории Планометрия.

Параллельное из кривой является

• огибающая семейства конгруэнтных окружностей с центром на кривой.

Он обобщает концепцию параллельных линий . Его также можно определить как

• кривая, точки которой находятся на фиксированном нормальном расстоянии от данной кривой.

Эти два определения не полностью эквивалентны, поскольку последнее предполагает гладкость , а первое - нет.

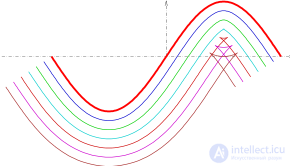
параллельные кривые графика на расстояния

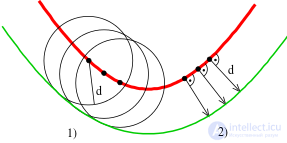
Два определения параллельной кривой: 1) огибающая семейства конгруэнтных окружностей, 2) фиксированное нормальное расстояние

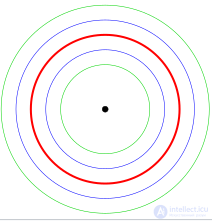
Параллельные кривые круга (красный) тоже круги

В системе автоматизированного проектирования предпочтительным термином для параллельной кривой является кривая смещения . (В других геометрических контекстах термин «смещение» также может относиться к переносу . ) Кривые смещения важны, например, при обработке с числовым программным управлением , где они описывают, например, форму выполненного резания. круглым режущим инструментом двухкоординатного станка. Форма реза смещена от траектории резца на постоянное расстояние в направлении, перпендикулярном траектории резца в каждой точке.

В области компьютерной 2D- графики, известной как векторная графика , (приблизительное) вычисление параллельных кривых задействовано в одной из фундаментальных операций рисования, называемых штриховкой, которая обычно применяется к полилиниям или полилинии (сами называемые контурами) в этом поле.

За исключением случая линии или круга , параллельные кривые имеют более сложную математическую структуру, чем кривая-прародительница. Например, даже если кривая-предшественница гладкая , ее смещения могут быть не такими; это свойство проиллюстрировано на верхнем рисунке с использованием синусоидальной кривой в качестве кривой-предшественницы. В общем, даже если кривая рациональна , ее смещения могут быть не такими. Например, смещения параболы являются рациональными кривыми, но смещения эллипса или гиперболы не рациональны, даже если сами эти исходные кривые рациональны.

Это понятие также распространяется на 3D- поверхности , где оно называется смещенной поверхностью . Увеличение твердого объема за счет (постоянного) смещения расстояния иногда называют растяжением . Противоположную операцию иногда называют обстрелом . Смещенные поверхности важны при обработке с числовым программным управлением , где они описывают форму реза, выполненного концевой фрезой со сферической головкой на трехосном станке. ^[10] Другие формы режущих коронок могут быть смоделированы математически с помощью общих поверхностей смещения. ^[11]

параллельная кривая параметрически заданной кривой

Если существует регулярное параметрическое представление данной доступной кривой, второе определение параллельной кривой (см. выше) приводит к следующему параметрическому представлению параллельной кривой с расстоянием :

с блоком нормальный .

В декартовых координатах:

Параметр расстояния тоже может быть отрицательным. В этом случае получается параллельная кривая на противоположной стороне кривой (см. Диаграмму на параллельных кривых окружности). Легко проверить: параллельная кривая прямой - это параллельная линия в обычном смысле, а параллельная кривая окружности - это концентрическая окружность.

Геометрические свойства:

• это означает: касательные векторы для фиксированного параметра параллельны.
• с участием кривизны данной кривой и кривизна параллельной кривой для параметра .
• с участием радиус кривизны данной кривой и радиус кривизны параллельной кривой для параметра .

• Что касается параллельных прямых , нормальная линия к кривой также нормальна к ее параллелям.
• При построении параллельных кривых они будут иметь выступы, когда расстояние от кривой совпадает с радиусом кривизны . Это точки, где кривая касается эволюции .
• Если кривая-предшественница является границей плоского множества, а его параллельная кривая не имеет самопересечений, то последняя является границей суммы Минковского плоского множества и диска данного радиуса.

Если данная кривая полиномиальна (то есть а также являются полиномами), то параллельные кривые обычно не являются полиномами. В области САПР это недостаток, потому что системы САПР используют полиномы или рациональные кривые. Чтобы получить хотя бы рациональные кривые, квадратный корень из представления параллельной кривой должен быть разрешимым. Такие кривые называются кривыми пифагора годографа и исследованы Р. Т. Фаруки. ^[13]

Параллельные кривые неявной кривой

Как правило, аналитическое представление параллельной кривой неявной кривой невозможно. Только для простых случаев прямых и окружностей можно легко описать параллельные кривые. Например:

Линия → функция расстояния: (Нормальная форма Гессе)

Круг → функция расстояния:

Вообще говоря, предполагая определенные условия, можно доказать существование ориентированной функции расстояния . На практике приходится относиться к этому численно. ^[14] Рассматривая параллельные кривые, верно следующее:

• Параллельная кривая для расстояния d - это установленный уровень соответствующей ориентированной функции расстояния .

Свойства функции расстояния:

• 
• 
• 

Пример: на
схеме показаны параллельные кривые неявной кривой с уравнением
Примечание: кривые не являются параллельными кривыми, потому что не соответствует действительности в интересующей области.

Дальнейшие примеры

• В эвольвенты данной кривой представляют собой набор параллельных кривых. Например: эвольвенты окружности - это параллельные спирали (см. Диаграмму).

И: ^[16]

• Параболы имеют в качестве (двусторонний) смещают рациональные кривой степени 6.
• Гиперболу или эллипс имеет в качестве (двусторонний) смещает в алгебраической кривой степени 8.
• Кривая Безье степени п имеет в качестве (двусторонний) смещает алгебраических кривых степени 4 п - 2 . В частности, кубическая кривая Безье имеет в качестве (двусторонних) смещений алгебраические кривые степени 10.

Параллельная кривая кривой с углом

При определении траектории резания детали с острым углом для обработки вы должны определить кривую, параллельную (смещенной) заданной кривой, которая имеет прерывистую нормаль в углу. Даже если данная кривая не является гладкой в ​​остром углу, ее параллельная кривая может быть гладкой с непрерывной нормалью или может иметь изломы, когда расстояние от кривой совпадает с радиусом кривизны в остром углу.

Обычные фанаты [ править ]

Как описано выше , параметрическое представление параллельной кривой,, к заданной кривой, , с расстоянием является:

с блоком нормальный .

В остром углу () нормаль к данный разрывной, что означает односторонний предел нормали слева не равняется до предела справа . Об этом говорит сайт https://intellect.icu . Математически,

.

Однако мы можем определить нормальный веер ^[11] который обеспечивает интерполянт между а также , и используйте на месте в остром углу:

где .

Полученное определение параллельной кривой обеспечивает желаемое поведение:

Алгоритмы

Эффективным алгоритмом компенсации является уровневый подход, описанный Кимелем и Брукштейном (1993). ^[17]

Для этой задачи существует множество приближенных алгоритмов. Обзор 1997 года см. В книге Элбера, Ли и Кима «Сравнение методов аппроксимации кривой смещения». ^[18]

Параллельные (смещенные) поверхности

Смещенные поверхности важны при обработке с числовым программным управлением , где они описывают форму реза, выполненного концевой фрезой со сферическим концом трехосевой фрезы. ^[10] Если существует регулярное параметрическое представление данной доступной поверхности, второе определение параллельной кривой (см. выше) обобщается до следующего параметрического представления параллельной поверхности с расстоянием :

с блоком нормальный .

Параметр расстояния тоже может быть отрицательным. В этом случае получается параллельная поверхность на противоположной стороне поверхности (см. Аналогичную диаграмму на параллельных кривых окружности). Легко проверить: параллельная поверхность плоскости - это параллельная плоскость в обычном смысле, а параллельная поверхность сферы - это концентрическая сфера.

Геометрические свойства:

• это означает: касательные векторы для фиксированных параметров параллельны.
• это означает: векторы нормали для фиксированных параметров совпадают с направлением.
• где а также являются операторами формы для а также соответственно.

Главные кривизны являются собственными значениями этого оператора формы , главные направления кривизны являются его собственными векторами , то гауссова кривизна является определяющей , а средняя кривизна равна половина его след .

• где а также являются обратными операторам формы для а также соответственно.

Главные радиусы кривизны являются собственными значениями обратного оператора формы , главные направления кривизны являются его собственными векторами , обратная величина гауссовой кривизны является его определителем , а средний радиус кривизны составляет половину его следа .

Обратите внимание на сходство с геометрическими свойствами параллельных кривых .

Обобщения

Проблема довольно очевидно обобщается на большие размеры, например, на смещенные поверхности, и несколько менее тривиально на поверхности труб . ^[20] Обратите внимание, что терминология для многомерных версий варьируется даже шире, чем в плоском случае, например, другие авторы говорят о параллельных волокнах, лентах и ​​трубках. ^[21] Для кривых, встроенных в 3D-поверхности, смещение может производиться по геодезической . ^[22]

Другой способ обобщить это (даже в 2D) - рассмотреть переменное расстояние, например, параметризованное другой кривой. ^[19] Можно, например, обводить (конверт) эллипсом вместо круга ^[19], как это возможно, например, в METAFONT . ^[23]

Совсем недавно Adobe Illustrator добавил несколько аналогичных возможностей в версию CS5 , хотя контрольные точки для переменной ширины указаны визуально. ^[24] В контекстах, где важно различать постоянное и переменное смещение расстояния, иногда используются аббревиатуры CDO и VDO.

Общие кривые смещения

Предположим, у вас есть регулярное параметрическое представление кривой, , и у вас есть вторая кривая, которая может быть параметризована ее единичной нормалью, , где нормаль (эта параметризация нормалью существует для кривых, кривизна которых строго положительна или отрицательна и, следовательно, выпуклая, гладкая и непрямая). Параметрическое представление общей кривой смещения компенсируется является:

где единица нормали .

Обратите внимание, что тривиальное смещение, , дает вам обычные параллельные (иначе говоря, смещенные) кривые.

Геометрические свойства:

• это означает: касательные векторы для фиксированного параметра параллельны.
• Что касается параллельных прямых , нормаль к кривой также нормальна к ее общим смещениям.
• с участием кривизна общей кривой смещения, кривизна , а также кривизна для параметра .
• с участием радиус кривизны общей кривой смещения, радиус кривизны , а также радиус кривизны для параметра .
• При построении общих кривых смещения они будут иметь выступы, когда кривизна кривой совпадает с кривизной смещения. Это точки, где кривая касается эволюции .

Поверхности общего смещения

Общие смещенные поверхности описывают форму резов, выполненных различными режущими головками, используемыми трехосными концевыми фрезами при обработке с числовым программным управлением . ^[11] Предположим, у вас есть регулярное параметрическое представление поверхности,, и у вас есть вторая поверхность, которая может быть параметризована ее единичной нормалью, , где нормаль (эта параметризация нормалью существует для поверхностей, гауссова кривизна которых строго положительна и, следовательно, выпуклая, гладкая и не плоская). Параметрическое представление общей офсетной поверхности компенсируется является:

где единица нормали .

Обратите внимание, что тривиальное смещение, , дает вам обычные параллельные (иначе говоря, смещенные) поверхности.

Геометрические свойства:

• Что касается параллельных прямых , касательная плоскость поверхности параллельна касательной плоскости ее общих смещений.
• Что касается параллельных прямых , нормаль к поверхности также нормальна к ее общим смещениям.
• где а также являются операторами формы для а также соответственно.

Главные кривизны являются собственными значениями этого оператора формы , главные направления кривизны являются его собственными векторами , то гауссова кривизна является определяющей , а средняя кривизна равна половина его след .

• где а также являются обратными операторам формы для а также соответственно.

Главные радиусы кривизны являются собственными значениями обратного оператора формы , главные направления кривизны являются его собственными векторами , обратная величина гауссовой кривизны является его определителем , а средний радиус кривизны составляет половину его следа .

Обратите внимание на сходство с геометрическими свойствами общих кривых смещения .

Вывод геометрических свойств для общих выносов [ править ]

Геометрические свойства, перечисленные выше для общих кривых и поверхностей смещения, могут быть получены для смещений произвольного размера. Предположим, у вас есть регулярное параметрическое представление n-мерной поверхности,, где размерность это n-1. Также предположим, что у вас есть вторая n-мерная поверхность, которая может быть параметризована ее единичной нормалью,, где нормаль (эта параметризация нормалью существует для поверхностей, гауссова кривизна которых строго положительна и, следовательно, выпуклая, гладкая и не плоская). Параметрическое представление общей офсетной поверхности компенсируется является:

где единица нормали . (Тривиальное смещение,, дает обычные параллельные поверхности.)

Во-первых, обратите внимание, что нормальный нормальный по определению. Теперь применим дифференциал по к , который дает нам его касательные векторы, покрывающие его касательную плоскость.

Обратите внимание, касательные векторы для являются суммой касательных векторов для и его смещение , которые используют одну и ту же единицу нормально. Таким образом, общая поверхность смещения имеет одну касательную плоскость и нормаль с а также . Это соответствует природе конвертов.

Теперь рассмотрим уравнения Вейнгартена для оператора формы , которые можно записать как. Если обратимо, . Напомним, что главные кривизны поверхности - это собственные значения оператора формы, главные направления кривизны - его собственные векторы , кривизна Гаусса - его определитель , а средняя кривизна - половина его следа . Обратный к оператору формы сохраняет те же значения для радиусов кривизны.

Подставляя в уравнение для дифференциала , мы получили:

где оператор формы для .

Затем мы снова используем уравнения Вейнгартена, чтобы заменить:

где оператор формы для .

Затем мы решаем для и умножить обе стороны на чтобы вернуться к уравнениям Вейнгартена , на этот раз для:

Таким образом, , и инвертирование обеих сторон дает нам, .

эквидистанта

Параллельная кривая или эквидистанта плоской кривой — огибающая семейства окружностей равного радиуса, центры которых лежат на заданной кривой. Понятие параллельной кривой — обобщение понятия параллельной прямой на случай плоских кривых.

Для параметрически заданной кривой параллельная кривая, проходящая на расстоянии от данной определяется уравнениями

,

.

Или в векторной форме:

,

где матрица соответствует повороту вектора на 90° по часовой стрелке.

Свойства эквидистанты

• Ориентированная кривизна параллельной кривой выражается через кривизну исходной кривой по формуле

  

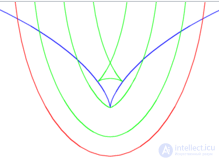
Эллипс (красный), его эволюта (синий) и несколько параллельных кривых (зеленый). Обратите внимание, как изламываются параллельные кривые при встрече с эволютой

Вау!! 😲 Ты еще не читал? Это зря!

• Отображение рельефа (горизонталь)
• Функция расстояния и подписана функция расстояния
• Поле расстояния
• Эволюта
• Эвольвента
• пареллельность
• параллельные прямые
• антипареллельность
• параллельные прямая и плоскость
• параллельные плоскости

Исследование, описанное в статье про параллельные кривые, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое параллельные кривые, параллельная кривая и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия