Признак параллельности прямых кратко

Привет, мой друг, тебе интересно узнать все про признак параллельности прямых, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое признак параллельности прямых , настоятельно рекомендую прочитать все из категории Планометрия.

Теорема

Если внутренние накрест лежащие углы равны, то прямые параллельны

Признаки параллельных прямых

1. Если две прямые параллельны третьей прямой, то они являются параллельными:

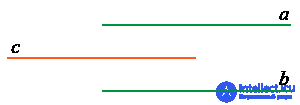
Если a || c и b || c, то a || b.

2. Если две прямые перпендикулярны третьей прямой, то они параллельны:

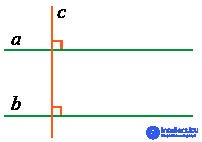
Если a ⊥ c и b ⊥ c, то a || b.

Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.

3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:

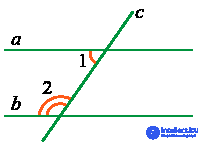
Если ∠1 + ∠2 = 180°, то a || b.

4. Об этом говорит сайт https://intellect.icu . Если соответственные углы равны, то прямые параллельны:

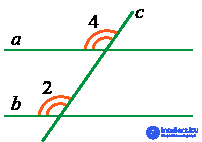
Если ∠2 = ∠4, то a || b.

5. Если внутренние накрест лежащие углы равны, то прямые параллельны:

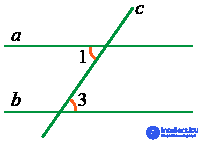
Если ∠1 = ∠3, то a || b.

Свойства параллельных прямых

Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.

1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:

Если a || b, то ∠1 + ∠2 = 180°.

2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:

Если a || b, то ∠2 = ∠4.

3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:

Если a || b, то ∠1 = ∠3.

Следующее свойство является частным случаем для каждого предыдущего:

4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

Если a || b и c ⊥ a, то c ⊥ b.

Пятое свойство — это аксиома параллельности прямых:

5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:

Вау!! 😲 Ты еще не читал? Это зря!

• антипараллельность , антипараллельные прямые ,

Я хотел бы услышать твое мнение про признак параллельности прямых Надеюсь, что теперь ты понял что такое признак параллельности прямых и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия

Из статьи мы узнали кратко, но содержательно про признак параллельности прямых