Привет, сегодня поговорим про длина окружности, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
длина окружности , настоятельно рекомендую прочитать все из категории Планометрия.
При неограниченном увеличении сторон правильного многоугольника его периметр приближается к периметру окружности.
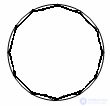Теорема Отношение длины окружности к ее радиусу не зависит от окружности.
Доказательство. Возьмем две произвольные окружности с радиусами R1 и R2 и длинами l1 и l2. Об этом говорит сайт https://intellect.icu . предположим, что
Впишем в окружности правильные n-угольники. N настолько велико, что периметры p1 и p2 правильных многоугольников приближаются к длинам окружностей l1 и l2. Поэтому заменим длины окружностей на периметры, тогда
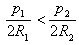
Но периметры правильных выпуклых n-угольников относятся как радиусы описанных окружностей:
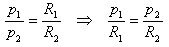
Что противоречит предположению. Теорема доказана.
Отношение длины окружности к диаметру обозначается греческой буквой π.
Я что-то не договорил про длина окружности, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое длина окружности
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Планометрия
Из статьи мы узнали кратко, но содержательно про длина окружности
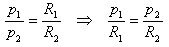
Комментарии