Привет, сегодня поговорим про свойства движения, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
свойства движения , настоятельно рекомендую прочитать все из категории Планометрия.
Теорема. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Доказательство. Пусть есть три точки A, B и С, которые лежат на одной прямой и точка B лежит между точками A и С.
Докажем, что точки A`, B` и C` лежат на одной прямой.
Если точки A`, B` и C` не лежат на одной прямой, то эти точки являются вершинами треугольника. Поэтому A`C`<a`b`+b`c`. По="" определению="" движения="" следует,="" что="" ac<ab+bc,="" но="" по="" свойству="" измерения="" отрезков="" ac="AB+BC," противоречит="" нашему="" предположению,="" следовательно="" точка="" b`="" лежит="" на="" прямой="" a`c`.="" <br="">Докажем, что B` лежит между A` и C`. Об этом говорит сайт https://intellect.icu . Тогда выполняются равенства AB=A`B`, AC=A`C`, BC=B`C`, AB+BC=AC. Отсюда следует, что A`B`+B`C`=A`C`. Это означает, что точка B` лежит между точками A` и C`.Теорема доказана.
Следствие из теоремы
1.Отрезок движением переводится в отрезок.
2.Луч при движении переходит в луч, прямая – в прямую.
3.Треугольник движением переводится в треугольник.
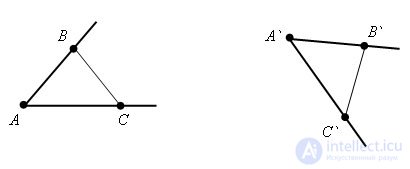
Теорема. При движении сохраняются углы между полупрямыми.
свойства движения " />
Пусть полупрямые AB и BC не лежат на одной прямой и образуют угол. При движении полупрямые переходят в A`B` и A`C` соответственно. Проведем отрезок BC и B`C`. Получим треугольник ABC и A`B`C`. Так как при движении расстояния сохраняются, то треугольники ABC и A`B`C` равны по третьему признаку равенства треугольников, а следовательно углы ABC и A`B`C` равны. Теорема доказана
Я что-то не договорил про свойства движения, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое свойства движения
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Планометрия
Из статьи мы узнали кратко, но содержательно про свойства движения
Комментарии