Высота, медиана, чевиана и биссектриса треугольника - замечательные отрезки треугольника

Лекция

Привет, мой друг, тебе интересно узнать все про высота треугольника, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое высота треугольника, медиана треугольника, биссектриса треугольника, замечательные отрезки треугольника, трисектриса, чевиана , настоятельно рекомендую прочитать все из категории Планометрия.

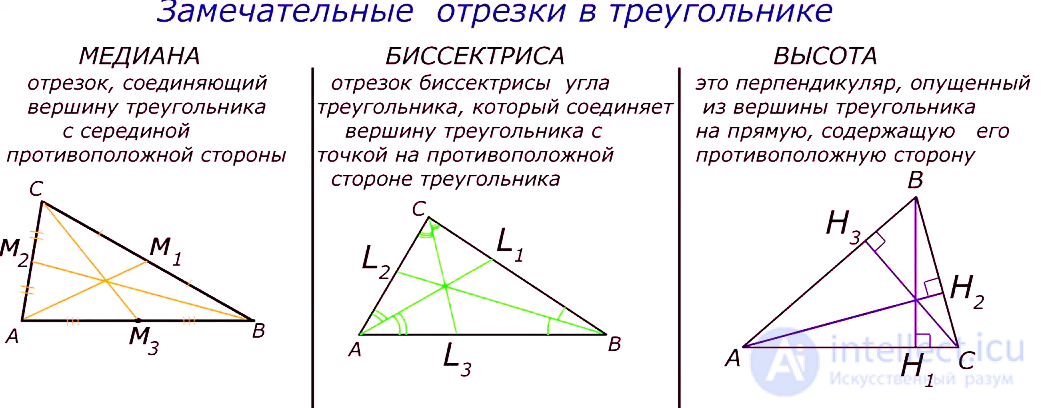Рассмотрим эти замечательные отрезки в треугольнике подробнее

высота треугольника

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.

Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины, к прямой, которая содержит противолежащую сторону треугольника.

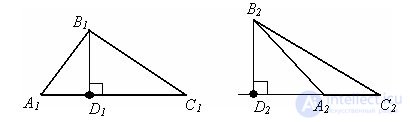
B1D1 – высота треугольника A1B1C1, опущенная из вершины B1. B2D2 – высота треугольника A2B2C2, опущенная из вершины B2.

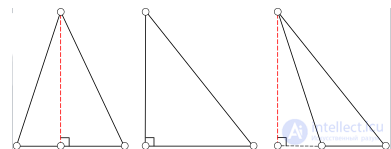
Высота в треугольниках различного типа

Свойства высоты треугольника

Свойства ортоцентра

Высоты треугольника

Все 3 высоты треугольника пересекаются в 1 точке, называемой ортоцентром. Доказательства ниже.
Ортоцентр изогонально сопряжен центру описанной окружности.
Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.

Свойства, связанные с описанной окружностью

Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
Если О — центр описанной окружности ΔABC, то ,
- $|OH| = \sqrt{9R^2-(a^2+b^2+c^2)}$ , где $R$ — радиус описанной окружности; $a,b,c$ — длины сторон треугольника.
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
Следствия теоремы Гамильтона:
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трех треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.

Свойства высот равнобедренного треугольника

Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
У равностороннего треугольника все три высоты равны.

Свойства оснований высот треугольника

Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
Описанная около ортотреугольника окружность - окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трех отрезков, соединяющих ортоцентр с вершинами треугольника.
Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек. Основания трех высот произвольного треугольника, середины трех его сторон (основания его внутренних медиан) и середины трех отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.

Свойства середин высот треугольника

Теорема Шлемильха. В 1860 году Шлемильх доказал теорему: три прямые, соединяющие середины сторон треугольника с серединами его соответствующих высот, пересекаются в одной точке. В 1937 году советский математик С. И. Зетель показал, что эта теорема верна не только для высот, но и для любых других чевиан.
Еще одна очевидная теорема. Середина высоты треугольника всегда лежит на пересекающей ее средней линии треугольника.
Теорема Ригби. Если к любой стороне остроугольного треугольника провести высоту и касающуюся ее с другой стороны вневписанную окружность, то точка касания последней с этой стороной, середина упомянутой высоты, а также инцентр лежат на одной прямой..
Из теоремы Ригби следует, что 3 отрезка, соединяющих середину каждой из 3 высот треугольника с точкой касания вневписанной окружности, проведенной к той же стороне, что и высота, пересекаются в инцентре.
Середины X и Y двух высот треугольника ABC, а также середина K стороны BC, из концов которой эти две высоты выходят, а также ортоцентр H лежат на одной окружности, на которой также лежит и пятая точка D - основание третьей высоты AD.

Другие свойства

Если треугольник разносторонний (неравносторонний), то его внутренняя биссектриса, проведенная из любой вершины, лежит между внутренними медианой и высотой, проведенными из той же вершины.
Высота треугольника изогонально сопряжена диаметру (радиусу) описанной окружности, проведенному из той же самой вершины.
В остроугольном треугольнике две его высоты отсекают от него 2 пары треугольников с 1 общей вершиной, которые подобны.
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Свойства минимальной из высот

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
Минимальная высота в треугольнике всегда проходит внутри этого треугольника.

Соотношения

$h_{a}=b\sin \gamma =c\sin \beta ,$
$h_{a}={\frac {2S}{a}},$ где $S$ — площадь треугольника, $a$ — длина стороны треугольника, на которую опущена высота.
$h_{a}^{2}={\frac {1}{2}}(b^{2}+c^{2}-{\frac {1}{2}}(a^{2}+{\frac {(b^{2}-c^{2})^{2}}{a^{2}}}))$
$h_{a}={\frac {bc}{2R}},$ где $bc$ — произведение боковых сторон, $R$ — радиус описанной окружности
$h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ac:ab$
${\frac 1{h_{a}}}+{\frac 1{h_{b}}}+{\frac 1{h_{c}}}={\frac {1}{r}}$ , где $r$ — радиус вписанной окружности.
$S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}$ , где $S$ — площадь треугольника.
$a={\frac {2}{h_{a}{\cdot }{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}$ , $a$ — сторона треугольника к которой опускается высота $h_{a}$ .
Высота равнобедренного треугольника, опущенная на основание:
$h_{c}={\frac {1}{2}}{\sqrt {4a^{2}-c^{2}}},$

где $c$ — основание, $a$ — боковая сторона.

$h={\frac {\sqrt {3}}{2}}a$ — высота в равностороннем треугольнике со стороной $a$ .

Теорема о высоте прямоугольного треугольника

Если высота в прямоугольном треугольнике $ABC$ длиной $h$ , проведенная из вершины прямого угла, делит гипотенузу длиной $c$ на отрезки $m$ и $n$ , соответствующие катетам $b$ и $a$ , то верны следующие равенства:

$h^{2}=mn$
$a^{2}=cn$ ; $b^{2}=cm$
$ch=ab$

Теорема о проекциях

См. с. 51, ф. (1.11-4). Теорема о проекциях: $c=a\cos \beta +b\cos \alpha ;\ a=b\cos \gamma +c\cos \beta ;\ b=c\cos \alpha +a\cos \gamma$ . Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины $C$ , делит противоположную ей сторону $c$ на две части $a\cos \beta$ и $b\cos \alpha$ , считая от вершины $A$ к $B$ .

Мнемоническое стихотворение

Высота похожа на кота,
Который выгнул спину
И под прямым углом
Соединил вершину
И сторону хвостом.

История высот треугольника

Утверждение: «Все 3 высоты треугольника пересекаются в одной точке», называемой теперь ортоцентром, в «Началах» Евклида отсутствует. Часть историков приписывает это утверждение Архимеду и называют его теоремой Архимеда. Ортоцентр впервые в греческой математике использован в «Книге лемм» Архимеда, хотя явного доказательства существования ортоцентра Архимед не привел.
В косвенной форме и в явном виде это утверждение («Все 3 высоты треугольника пересекаются в одной точке») встречается у Прокла (410-485) - комментатора Евклида.
Тем не менее до середины девятнадцатого века, ортоцентр нередко называли архимедовой точкой.
Другие историки математики считают автором первого доказательства Уильяма Чеппла (William Chapple (surveyor) (англ.)русск.) (Miscellanea Curiosa Mathematica, 1749 год).
Сам термин ортоцентр впервые был использован У. Х. Безантом (W. H. Besant (англ.)русск.) в работе "Конические сечения, исследованные геометрически (1869)" () .

Две составные части высоты: предвысота и поствысота

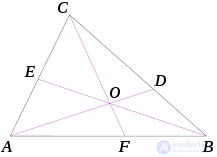
Три чевианы, проходящие через общую точку

На рис. справа в треугольнике ABC через точку O проведены 3 высоты: AD, BE и CF. Тогда точка O пересечения 3 высот разбивает каждую высоту на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем довысотой или предвысотой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем поствысотой.
Эти 2 термина введены по аналогии с операторами цикла с учетом их изображения на блок-схемах в информатике. Там есть понятия цикла соответственно с пред- и пост-условием в зависимости от того, стоит ли это условие перед или после тела цикла. У нас в роли тела цикла выступает точка O пересечения высот, а в роли условия – первый или второй конец отрезка, вводимого, как понятие для одной из двух частей высоты.
С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии.

Например, в любом треугольнике (в остро-, прямо-, и в тупоугольном) 3 произведения пред- и поствысоты совпадают . Для остро-и прямоугольного треугольников это утверждение легко доказываемое. Оно верно и для любого тупоугольного треугольника, что удивительно, поскольку в таком треугольнике 2 из 3 высот даже не лежат внутри самого треугольника.

Замечание. На этом рис. справа в треугольнике ABC чевианы не являются высотами. На следующем рис. справа в треугольнике ABC три высоты: $AH_{a},BH_{b},CH_{c}$

Высоты в треугольнике ABC

биссектриса треугольника

Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой противолежащей стороны.

биссектриса треугольника

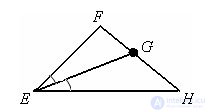
EG – биссектриса угла FEH. ∠ FEG = ∠ GEH.
Биссектриса (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудаленных от сторон этого угла

Связанные определения

Точка пересечения биссектрисы угла треугольника с его стороной, не являющейся стороной этого угла, называется основанием биссектрисы.

В любом треугольнике $ABC$ , кроме внутренних биссектрисы или просто биссектрис, можно провести и внешние биссектри́сы, то есть биссектрисы углов, смежных с внутренними углами треугольника. При этом внутренняя и внешняя биссектриса одного и того же угла перпендикулярны.
Проведение в данном треугольнике всех трех его внешних биссектрис до их точек пересечения друг с другом в центрах вневписанных окружностей (соответственно $J_{A},J_{B},J_{C}$ ) образует новый треугольник (см. рис.) — треугольник трех внешних биссектрис. Это — новый треугольник центров вневписанных окружностей с вершинами $J_{A},J_{B},J_{C}$ , которые касаются соответственно сторон $a,b,c$ исходного треугольника.
Центр окружности, проходящей через центры вневписанных окружностей — точка Бевэна.
Исходный треугольник является ортотреугольником для треугольника $\Delta J_{A}J_{B}J_{C}$
Точка пересечения симедиан треугольника, образованного центрами его вневписанных окружностей $J_{A},J_{B},J_{C}$ , является центром эллипса МандАра. Об этом говорит сайт https://intellect.icu . Эту точку называют по-английски middlespoint, по-немецки — «Mittelpunkt». Она открыта в 1836-ом году Христианом Генрихом фон Нагелем (Christian Heinrich von Nagel).

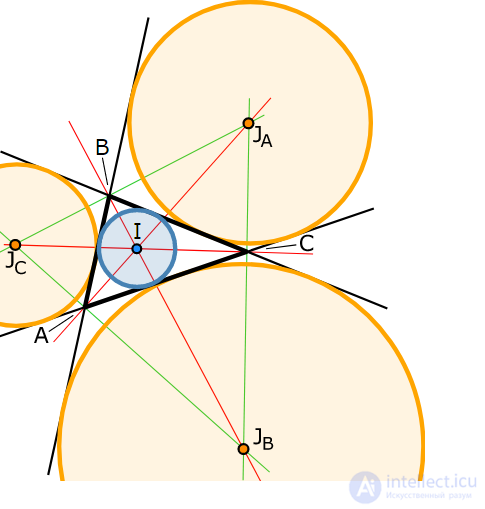
Центры трех вневписанных окружностей (соответственно $J_{A},J_{B},J_{C}$ ) образуют — треугольник трех внешних биссектрис

Построение биссектрисы

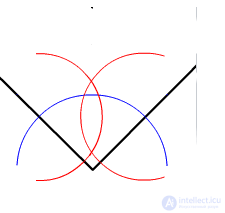
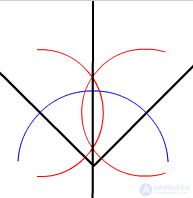
Свойства биссектрис

Свойства точек пересечения биссектрис

Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности (инцентре).
Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трех вневписанных окружностей этого треугольника.
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Ее центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.

Свойства, связанные с углами

Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.

Свойства, связанные с дугами

Свойство биссектрисы вписанного угла: биссектриса вписанного угла делит на две равные части дугу, на которую этот угол опирается.
То же свойство верно и для биссектрисы центрального угла.

Свойства биссектрис равнобедренного треугольника

Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной внутреннему углу стороне — основанию, если треугольник равнобедренный.
У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
У равностороннего треугольника все три внутренние биссектрисы равны.

Свойства оснований биссектрис

{\frac {BD}{CD}}={\frac {AB}{AC}}

или

{\frac {BD}{AB}}={\frac {CD}{AC}}

Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть ${\frac {BD}{CD}}={\frac {AB}{AC}}$ или ${\frac {BD}{AB}}={\frac {CD}{AC}}$ .
Теорема о биссектрисе — частный случай теоремы Штейнера.
Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
Через точку Фейербаха проходит окружность, проведенная через основания биссектрис .

Свойства осей биссектрис

Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
Точка Лемуана треугольника лежит на прямой Обера четырехсторонника, образованного четырьмя осями биссектрис.

Другие свойства

Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведенная из любой его вершины, лежит между внутренними медианой и высотой, проведенными из той же вершины.
Расстояния от сторон угла до любой точки биссектрисы одинаковы.
Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причем даже при наличии трисектора.
Три внешние биссектрисы любого треугольника пересекаются в трех разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трех внешних биссектрис исходного треугольника.

Длина биссектрис в треугольнике

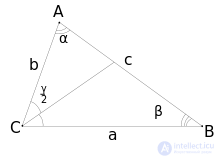
Биссектриса Треугольника ABC

Для выведения нижеприведенных формул можно воспользоваться теоремой Стюарта.

${\displaystyle l_{c}=<?php echo e(\sqrt {ab(a+b+c)(a+b-c)); ? data-auto-open loading=$ \over {a+b}}={\frac {2{\sqrt {abp(p-c)}}}{a+b}}}" class="mwe-math-fallback-image-inline" src="/th/25/blogs/id3334/0ee1ecd147d0458d0151fcabc7aedefe.svg" style="border:0px; display:inline-block; height:6.509ex; vertical-align:-2.171ex; width:49.215ex" />, где $p$ — полупериметр.

$l_{c}={\sqrt {ab-a_{l}b_{l}}}$

$l_{c}={\frac {2ab\cos {\frac {\gamma }{2}}}{a+b}}$

$l_{c}={\frac {h_{c}}{\cos {\frac {\alpha -\beta }{2}}}}$

Для трех биссектрис углов $A$ , $B$ и $C$ с длинами соответственно $l_{a},l_{b},$ и $l_{c}$ , справедлива формула

${\frac {(b+c)^{2}}{bc}}l_{a}^{2}+{\frac {(c+a)^{2}}{ca}}l_{b}^{2}+{\frac {(a+b)^{2}}{ab}}l_{c}^{2}=(a+b+c)^{2}.$ ,

$w_{c}^{2}=a_{w}\cdot b_{w}-ab=CE^{2}=BE\cdot AE-ab$ ,

Инцентр (точка пересечения трех внутренних биссектрис треугольника) делит внутреннюю биссектрису угла $A$ в отношении $\frac{b+c}{a}$ , где $a$ , $b$ , $c$ — стороны треугольника,

где:

$a,b,c$ — стороны треугольника против вершин $A,B,C$ соответственно,
$\alpha ,\beta ,\gamma$ — внутренние углы треугольника при вершинах $A,B,C$ соответственно,
$h_{c}$ — высота треугольника, опущенная на сторону $c$ .
$l_{c}$ — длина внутренней биссектрисы, проведенной к стороне $c$ ,
$a_{l},b_{l}$ — длины отрезков, на которые внутренняя биссектриса $l_{c}$ делит сторону $c$ ,
$w_{c}$ — длина внешней биссектрисы, проведенной из вершины $C$ к продолжению стороны $AB$ .
$a_{w},b_{w}$ — длины отрезков, на которые внешняя биссектриса $w_{c}$ делит сторону $c=AB$ и ее продолжение до основания самой биссектрисы.
Если медиана $m$ , высота $h$ и внутренняя биссектриса $t$ выходят из одной и той же вершины треугольника, около которого описана окружность радиуса $R$ , тогда^:p.122,#96

$4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).$

Длина частей биссектрис в треугольнике

Расстояние от вершины C до центра вписанной окружности равно $l_{c0}={\frac {r}{\sin({\frac {\gamma }{2}})}}={\sqrt {(p-c)^{2}+r^{2}}}={\sqrt {ab-4Rr}}$ , где R и r — радиусы описанной и вписанной окружностей, а γ — угол вершины C.
Формулы последнего пункта по сути дают длину части биссектрисы от вершины до точки их пересечения (до центра вписанной окружности или до инцентра).
Эту формулу и формулу для второй части внутренней биссектрисы можно также найти на основе следующего факта:
Инцентр делит внутреннюю биссектрису угла $A$ в отношении $\frac{b+c}{a}$ , где $a$ , $b$ , $c$ — стороны треугольника.

Уравнения биссектрис

Если две смежные стороны треугольника записаны уравнениями $y_{1}=a_{1}x+b_{1}$ и $y_{2}=a_{2}x+b_{2}$ , то в явном виде биссектрисы представимы в виде функций :

${\displaystyle y={\frac {a_{1}{\sqrt {a_{2}^{2}+1}}\pm a_{2}{\sqrt {a_{1}^{2}+1}}}<?php echo e(\sqrt {a_{2}^{2}+1); ? data-auto-open loading=$ \pm {\sqrt {a_{1}^{2}+1}}}}\,x+{\frac {b_{1}{\sqrt {a_{2}^{2}+1}}\pm b_{2}{\sqrt {a_{1}^{2}+1}}}\pm {\sqrt {a_{1}^{2}+1}}}}}" class="mwe-math-fallback-image-inline" src="/th/25/blogs/id3334/8fba847da56958c130f577b1e7f3b91d.svg" style="border:0px; display:inline-block; height:10.509ex; vertical-align:-4.671ex; width:59.278ex" />

Мнемоническое правило (шуточное)

Биссектриса — это крыса, которая бегает по углам и делит угол пополам.

медиана треугольника

Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противоположной стороны треугольника.

медиана треугольника

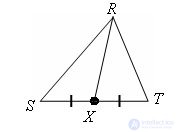
RX – медиана угла SRT. SX = XT

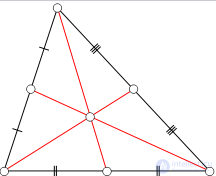
Треугольник и его медианы

Связанные определения с Медианой

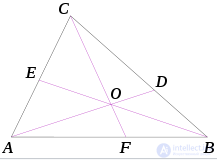
Три медианы, проходящие через общую точку

На рис. справа в треугольнике ABC через точку O проведены 3 медианы: AD, BE и CF. Тогда точка O пересечения 3 медиан разбивает каждую медиану на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем домедианой или предмедианой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем постмедианой. С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии. Например, в любом треугольнике отношение пред- и постмедианы равно двум.

Свойства Медиан

Основное свойство

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Свойства медиан равнобедренного треугольника

В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.

У равностороннего треугольника все три медианы равны.

Свойства оснований медиан

Окружность девяти точек

Теорема Эйлера для окружности девяти точек: основания трех высот произвольного треугольника, середины трех его сторон (основания его медиан) и середины трех отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
Теркем доказал теорему Теркема. Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (т. е. 3 высоты также обязаны пересечься в 1 точке).

Другие свойства

Если треугольник разносторонний (неравносторонний), то его биссектриса, проведенная из любой вершины, лежит между медианой и высотой, проведенными из той же вершины.
Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
В прямоугольном треугольнике медиана, проведенная из вершины с прямым углом, равняется половине гипотенузы.
Большей стороне треугольника соответствует меньшая медиана.
Отрезок прямой, симметричный или изогонально сопряженный внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
Медиана угла треугольника изотомически сопряжена самой себе.

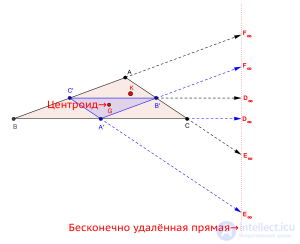
Бесконечно удаленная прямая — трилинейная поляра центроида

Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).

Основные соотношения Медиан

Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):

$m_{a}={\sqrt {\frac {2b^{2}+2c^{2}-a^{2}}{4}}},$

$m_{b}={\sqrt {\frac {2a^{2}+2c^{2}-b^{2}}{4}}},$

$m_{c}={\sqrt {\frac {2a^{2}+2b^{2}-c^{2}}{4}}},$

где $m_{a},\ m_{b},\ m_{c}$ — медианы к сторонам треугольника $a,\ b,\ c$ соответственно.

В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:

$m_{a}^{2}+m_{b}^{2}+m_{c}^{2}={\frac 34}(a^{2}+b^{2}+c^{2})$ .

Обратно, можно выразить длину произвольной стороны треугольника через медианы:

${\displaystyle a={\frac {2}{3}}{\sqrt {-m_{a}^{2}+2m_{b}^{2}+2m_{c}^{2}}}={\sqrt {2(b^{2}+c^{2})-4m_{a}^{2}}}={\sqrt <?php echo e(\frac {b^{2); ? data-auto-open loading=$ {2}}-c^{2}+2m_{b}^{2}}}={\sqrt {2}}-b^{2}+2m_{c}^{2}}},}" class="mwe-math-fallback-image-inline" src="/th/25/blogs/id3334/9e750941614382c382a739bc48fab989.svg" style="border:0px; display:inline-block; height:6.176ex; vertical-align:-2.171ex; width:91.553ex" />

${\displaystyle b={\frac {2}{3}}{\sqrt {-m_{b}^{2}+2m_{a}^{2}+2m_{c}^{2}}}={\sqrt {2(a^{2}+c^{2})-4m_{b}^{2}}}={\sqrt <?php echo e(\frac {a^{2); ? data-auto-open loading=$ {2}}-c^{2}+2m_{a}^{2}}}={\sqrt {2}}-a^{2}+2m_{c}^{2}}},}" class="mwe-math-fallback-image-inline" src="/th/25/blogs/id3334/266efc966780fec5f01ba2d2d6cdf252.svg" style="border:0px; display:inline-block; height:6.176ex; vertical-align:-2.171ex; width:92.018ex" />

${\displaystyle c={\frac {2}{3}}{\sqrt {-m_{c}^{2}+2m_{b}^{2}+2m_{a}^{2}}}={\sqrt {2(b^{2}+a^{2})-4m_{c}^{2}}}={\sqrt <?php echo e(\frac {b^{2); ? data-auto-open loading=$ {2}}-a^{2}+2m_{b}^{2}}}={\sqrt {2}}-b^{2}+2m_{a}^{2}}},}" class="mwe-math-fallback-image-inline" src="/th/25/blogs/id3334/4a80eba1fd5e6c9a27255e4e5bef672f.svg" style="border:0px; display:inline-block; height:6.176ex; vertical-align:-2.171ex; width:91.999ex" />

где $m_{a},m_{b},m_{c}$ — медианы к соответствующим сторонам треугольника, $a,b,c$ — стороны треугольника.

Площадь $S$ любого треугольника, выраженная через длины его медиан:

$S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}},$

где $\sigma =(m_{a}+m_{b}+m_{c})/2$ — полусумма длин медиан.

чевиана треугольника

Чевиана — это отрезок в треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне. Часто рассматриваются три таких отрезка, пересекающихся в одной точке, которые совместно называются чевианами. Название «чевиана» происходит от имени итальянского инженера Джованни Чевы, доказавшего известную теорему о чевианах, которая носит его имя. Медианы, биссектрисы и высоты в остроугольном треугольнике являются специальными случаями чевиан.

Длина чевианы

Треугольник с чевианой длины d

Теорема Стюарта

Длину чевианы можно найти по теореме Стюарта — длина чевианы d (см. рисунок) задается формулой

$\,b^{2}m+c^{2}n=a(d^{2}+mn).$

Медиана

Если чевиана является медианой (то есть делит сторону пополам), длина может быть определена по формуле

$m(b^{2}+c^{2})=a(d^{2}+m^{2})$

или

$2(b^{2}+c^{2})=4d^{2}+a^{2}$

поскольку

$a=2m.$

Следовательно,

$d={\frac {\sqrt {2b^{2}+2c^{2}-a^{2}}}{2}}.$

Биссектриса

Если чевиана является биссектрисой, ее длина удовлетворяет формуле

$\,(b+c)^{2}=a^{2}\left({\frac {d^{2}}{mn}}+1\right),$

$d^{2}+mn=bc$

откуда

$d={\frac {2{\sqrt {bcs(s-a)}}}{b+c}}$ ,

где полупериметр s = (a+b+c)/2.

Сторона a делится в пропорции b:c.

Высота

Если чевиана является высотой, а потому перпендикулярна стороне, ее длина удовлетворяет формулам

$\,d^{2}=b^{2}-n^{2}=c^{2}-m^{2}$

$d={\frac {2{\sqrt {s(s-a)(s-b)(s-c)}}}{a}},$

где полупериметр s = (a+b+c) / 2.

Свойства отношений

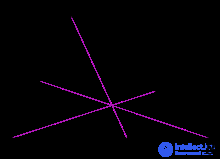
Три чевианы, проходящие через общую точку

Имеются различные свойства пропорций длин, образованных тремя чевианами, проходящими через одну общую внутреннюю точку. Для треугольника на рисунке справа выполняются равенства

${\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1;$ (Теорема Чевы)

${\frac {AO}{OD}}={\frac {AE}{EC}}+{\frac {AF}{FB}};$ (Теорема Ван-Обеля о треугольнике)

${\frac {OD}{AD}}+{\frac {OE}{BE}}+{\frac {OF}{CF}}=1;$ (Теорема Жергонна)

${\frac {AO}{AD}}+{\frac {BO}{BE}}+{\frac {CO}{CF}}=2.$ (Теорема Жергонна)

Два последних свойства эквивалентны, поскольку сумма этих двух уравнений дает тождество 1 + 1 + 1 = 3.

Делители периметра

Делители периметра треугольника — это чевиана, которая делит периметр пополам. Три таких делителя пересекаются в точке Нагеля треугольника.

Делители площади

Три делителя (пополам) площади треугольника — это его медианы.

Трисектрисы

Если в каждой вершине треугольника проведены две чевианы, делящие углы на три равные части, то шесть чевиан пересекаются попарно, образуя правильный треугольник, называемый треугольником Морли.

Площадь внутреннего треугольника, образованного чевианами

Теорема Рауса определяет отношение площади заданного треугольника к площади треугольника, образованного попарным пересечением трех чевиан, по одной из каждой вершины.

Вау!! 😲 Ты еще не читал? Это зря!

Антибиссектриса
Инцентр
Симедиана

Теорема Менелая

Теорема о биссектрисе
Ось внешних биссектрис или антиортовая ось
Треугольник
Треугольник трех внешних биссектрис
Центроид
Ортоцентр
замечательные отрезки треугольника

Теорема Менелая

Я что-то не договорил про высота треугольника, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое высота треугольника, медиана треугольника, биссектриса треугольника, замечательные отрезки треугольника, трисектриса, чевиана и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия

Высота, медиана, чевиана и биссектриса треугольника - замечательные отрезки треугольника

высота треугольника

Свойства высоты треугольника

Свойства ортоцентра

Свойства, связанные с описанной окружностью

Свойства высот равнобедренного треугольника

Свойства оснований высот треугольника

Свойства середин высот треугольника

Другие свойства

Свойства минимальной из высот

Соотношения

Теорема о высоте прямоугольного треугольника

Теорема о проекциях

Мнемоническое стихотворение

История высот треугольника

Две составные части высоты: предвысота и поствысота

биссектриса треугольника

Связанные определения

Свойства биссектрис

Свойства точек пересечения биссектрис

Свойства, связанные с углами

Свойства, связанные с дугами

Свойства биссектрис равнобедренного треугольника

Свойства оснований биссектрис

Свойства осей биссектрис

Другие свойства

Длина биссектрис в треугольнике

Длина частей биссектрис в треугольнике

Уравнения биссектрис

Мнемоническое правило (шуточное)

медиана треугольника

Связанные определения с Медианой

Свойства Медиан

Основное свойство

Свойства медиан равнобедренного треугольника

Свойства оснований медиан

Другие свойства

Основные соотношения Медиан

чевиана треугольника

Теорема Стюарта

Медиана

Биссектриса

Высота

Свойства отношений

Делители периметра

Делители площади

Трисектрисы

Площадь внутреннего треугольника, образованного чевианами

Вау!! 😲 Ты еще не читал? Это зря!

Комментарии

Оставить комментарий

Планометрия

Термины: Планометрия