Специальные и замечательные прямые и точки четырёхугольника кратко

Привет, Вы узнаете о том , что такое специальные прямые линии четырёхугольника, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое специальные прямые линии четырёхугольника, специальные точки четырёхугольника , настоятельно рекомендую прочитать все из категории Планометрия.

Специальные (замечательные) прямые линии четырехугольника

Средние линии четырехугольника

Пусть G, I, H, J — середины сторон выпуклого четырехугольника ABCD, а E, F — середины его диагоналей. Назовем три отрезка GH, IJ, EF соответственно первой, второй и третьей средними линиями четырехугольника. Первые две из них также называют бимедианами .

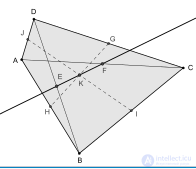
Точки E, K, F лежат на одной прямой, прямой Ньютона

Теоремы о средних линиях четырехугольника

• Обобщенная теорема Ньютона. Все три средние линии четырехугольника пересекаются в одной точке (в центроиде вершин («vertex centroid») четырехугольника) и делятся ею пополам.
• Середины E и F двух диагоналей, а также центроид вершин K выпуклого четырехугольника лежат на одной прямой EF. Указанная прямая называется прямой Ньютона.
• Заметим, что прямая Ньютона — Гаусса совпадает с прямой Ньютона, ибо обе проходят через середины диагоналей.
• Теорема Вариньона:
  • Четырехугольники GIHJ, EHFG, JEIF являются параллелограммами и называются параллелограммами Вариньона. Первый из них назовем большим параллелограммом Вариньона
  • Центрами этих 3 параллелограммов Вариньона назовем точки пересечения их пар диагоналей.
  • Центры всех 3 параллелограммов Вариньона лежат в 1 точке - на середине отрезка, соединяющего середины сторон исходного четырехугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).
  • Периметр большого параллелограмма Вариньона равен сумме диагоналей исходного четырехугольника.
  • Площадь большого параллелограмма Вариньона равна половине площади исходного четырехугольника , то есть

    .

  • Площадь исходного четырехугольника равна произведению первой и второй средних линий четырехугольника на синус угла между ними, то есть

    .

  • Сумма квадратов трех средних линий четырехугольника равна четверти суммы квадратов всех его сторон и диагоналей:

    .

• Формула Эйлера: учетверенный квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырехугольника минус сумма квадратов его диагоналей.
• Математически для рисунка слева с серым четырехугольником ABCD формула Эйлера записывается в виде:

  .

Прямая Ньютона

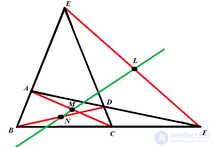
Прямая, получаемая соединением середин диагоналей (L, M и N), называется прямой Ньютона — Гаусса (зеленая)

• Если в четырехугольнике две пары противоположных сторон не параллельны, то две середины его диагоналей лежат на прямой, которая проходит через середину отрезка, соединяющего две точки пересечения этих двух пар противоположных сторон (на рисунке точки показаны красным цветом). Об этом говорит сайт https://intellect.icu . Указанная прямая называется прямой Ньютона (на рисунке она показана зеленым цветом). При этом прямая Ньютона всегда перпендикулярна прямой Обера.
• Точки, лежащие на прямой Ньютона, удовлетворяют теореме Анна.

Ортополярные линии ортополюсов троек вершин четырехугольника

Если задана фиксированная прямая линия ℓ, и выбрана любая из трех вершин четырехугольника , то все ортополюсы данной прямой линии ℓ относительно всех таких треугольников лежат на одной прямой. Эта линия называется ортополярной линией для данной линии ℓ относительно четырехугольника .

Специальные (замечательные) точки четырехугольника

Центроид четырехугольника

• Четыре отрезка, каждый из которых соединяет вершину четырехугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырехугольника и делятся им в отношении 3:1, считая от вершин.
• Вау!! 😲 Ты еще не читал? Это зря! свойства центроида четырехугольника.

Точка Понселе четырехугольника

Внутри четырехугольника существует точка Понселе (см. параграф "Окружности девяти точек треугольников внутри четырехугольника").

Точка Микеля четырехугольника

Внутри четырехугольника существует точка Микеля.

Вау!! 😲 Ты еще не читал? Это зря!

• Четырехугольники

Исследование, описанное в статье про специальные прямые линии четырёхугольника, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое специальные прямые линии четырёхугольника, специальные точки четырёхугольника и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия