Лекция
Привет, сегодня поговорим про площадь фигуры, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое площадь фигуры , настоятельно рекомендую прочитать все из категории Планометрия.
Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников.
Определение понятия площади стали давать много позже.
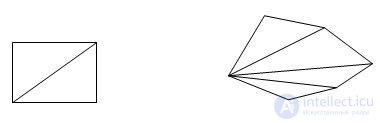
Фигура называется простой, если ее можно разбить на конечное число плоских треугольников.
Для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами:
1. Равные фигуры имеют равные площади;
2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей.
3. Площадь квадрата со стороной, равной единице измерения, равна единице.
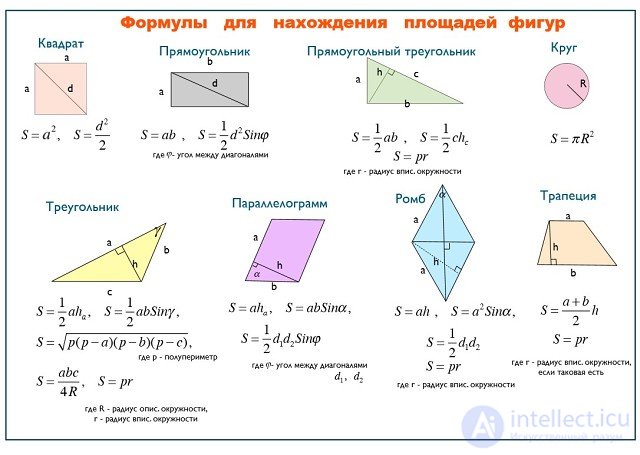
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Формальное введение понятия площадь и объем можно найти в статье мера Жордана, здесь мы приводим лишь наметки определения с комментариями.
Площадь — это вещественнозначная функция, определенная на определенном классе фигур евклидовой плоскости и удовлетворяющая четырем условиям:
При этом определенный класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
Чаще всего за «определенный класс» берут множество квадрируемых фигур. Фигура называется квадрируемой, если для любого
существует пара многоугольников
и
, такие что
и
, где
обозначает площадь
.
Примеры квадрируемых фигур
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | ||
| Треугольник | Формула Герона. |
|
| Треугольник | ||
| Треугольник | ||
| Квадрат | ||
| Прямоугольник | ||
| Ромб | ||
| Параллелограмм | ||
| Трапеция | ||
| Четырехугольник | ||
| Правильный шестиугольник | } |
|
| Правильный восьмиугольник | ||
| Правильный многоугольник | ||
| Произвольный многоугольник | Формула площади Гаусса |
|
| Круг | ||
| Сектор круга | ||
| Эллипс | b} |
На практике чаще всего требуется определить площадь ограниченной фигуры с кусочно-гладкой границей. Об этом говорит сайт https://intellect.icu . Математический анализ предлагает универсальный метод решения подобных задач.
Площадь, заключенная между графиком непрерывной функции на интервале и горизонтальной осью, может быть вычислена как определенный интеграл от этой функции:
Площадь, заключенная между графиками двух непрерывных функций на интервале
находится как разность определенных интегралов от этих функций:
В полярных координатах: площадь, ограниченная графиком функции и лучами
вычисляется по формуле:
.
Для определения площади кусочно гладкой поверхности в трехмерном пространстве используют ортогональные проекции к касательным плоскостям в каждой точке, после чего выполняют предельный переход. В результате, площадь искривленной поверхности A, заданной вектор-функцией , дается двойным интегралом :
То же в координатах:
Здесь .
Теория площадей занимается изучением обобщений, связанных с распространением определения k-мерной площади с кусочно-гладкого погружения на более общие пространства. Для кусочно-гладкого погружения f площадь определяют способом, аналогичным указанному выше, при этом у площади сохраняются такие свойства как положительность, аддитивность, нормированность, а также ряд новых.
Мерами земли при налоговых расчетах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли: коробья, веревка, жеребья и др.
Многие годы площадь считалась первичным понятием, не требующим определения. Основной задачей математиков являлось вычисление площади, при этом были известны основные свойства площади . В Древнем Египте использовались точные правила вычисления площади прямоугольников, прямоугольных треугольников и трапеций, площадь произвольного четырехугольника определялась приближенно как произведение полусумм пар противоположных сторон. Применение такой приближенной формулы связано с тем, что участки, площадь которых надо было померить, были в основном близки к прямоугольным и погрешность в таком случае оставалась небольшой. Историк математики А. П. Юшкевич предполагает, что египтяне могли и не знать, что пользуются приближенной формулой. В задаче 50 папируса Ринда содержится формула вычисления площади круга, которая считалась равной площади квадрата со стороной 8/9 диаметра круга . Такими же формулами пользовались и в Вавилоне, однако для площади круга приближение было менее точным. Кроме того, вавилоняне могли приближенно посчитать площади правильных пяти-, шести- и семиугольника со стороной равной единице. В шестидесятиричной системе им соответствовали 1,40, 2,37,20 и 3,41, соответственно .
Основным приемом вычисления площади при этом являлось построение квадрата, площадь которого равна площади заданной многоугольной фигуры, в частности в книге I «Начал» Евклида, которая посвящена планиметрии прямолинейных фигур, доказывается, что треугольник равновелик половине прямоугольника, имеющего с ним равные основания и высоту . Метод разложения, основанный на том, что две равносоставленные фигуры равновелики, позволял также вычислить площади параллелограммов и любых многоугольников .
Следующим шагом было вычисление площадей круга, кругового сектора, лунок и других фигур. Основу вычислений при этом составлял метод исчерпывания многоугольниками , с которого берет начало теория пределов. Метод заключается в построении последовательности площадей, которые при постепенном нарастании «исчерпывают» требуемую площадь. Метод исчерпывания, получивший свое название только в XVII веке, основан на аксиоме непрерывности Евдокса — Архимеда и приписывается Евдоксу Книдскому, который с его помощью показал, что площади кругов относятся друг к другу как квадраты их диаметров. Метод описан в «Началах» Евклида: аксиома Евдокса сформулирована в книге V, а сам метод исчерпывания и основанные на нем отношения — в книге XII . Особого совершенства в применении метода достиг Архимед, который с его помощью посчитал площадь сегмента параболы и другие[10][11]. Труд Архимеда «О спиралях» включает много утверждений, касающихся площадей различных витков спирали и их отношений[12]. Архимеду принадлежит идея использования площадей или объемов как вписанных, так и описанных фигур для определения требуемой площади или объема[13].
Индийцы поначалу пользовались той же формулой для вычисления четырехугольников, что египтяне и греки. Брахмагупта пользовался формулой для площади четырехугольников, выраженной через его полупериметр., которая верна для вписанного в окружность четырехугольника. Формулы вычисления площади обычно не доказывались, но демонстрировались с наглядными рисунками[14]. Формула Брахмагупты представляет собой аналог формулы Герона для площади треугольника, которую тот привел в своей «Метрике»[15].
Развитие и обобщение метода исчерпывания произошло только в XVII веке. В 1604 году в работе «Три книги о центре тяжести тел» Валерио широко использует теорему, по которой разность между площадями вписанной и описанной фигур, составленных из параллелограммов можно сделать меньше любой данной площади[16]. Настоящий прорыв был сделан Кеплером, которому для астрономических расчетов нужно было уметь вычислять площадь эллипса. Кеплер рассматривал площадь как «сумму линий» и, разлиновывая эллипс с шагом в один градус, показал[17], что . Кавальери, обосновывая подобный метод, названный «методом неделимых», сравнивал площади плоских фигур, используя сечение фигур параллельными прямыми[18]. Применение первообразной для нахождения площади плоской фигуры является наиболее универсальным методом. С помощью первообразной доказывается принцип Кавальери, по которому две плоские фигуры имеют равную площадь, если при пересечении каждой из них прямой, параллельной фиксированной, получаются отрезки одинаковой длины. Принцип был известен задолго до формирования интегрального исчисления .
Вычислением площадей кривых поверхностей занимался Архимед, определив, в частности, площадь поверхности шара[13]. В общем случае для определения площади поверхности нельзя пользоваться ни разверткой (не подходит для сферы), ни приближением многогранными поверхностями, то есть аналогом метода исчерпывания. Последнее показал Шварц, построив для боковой последовательности цилиндра последовательности, которые приводят к разным результатам (так называемый сапог Шварца) [19].
Общий прием вычисления площади поверхности на рубеже XIX—XX веков предложил Минковский, который для каждой поверхности строил «окутывающий слой» малой постоянной толщины, тогда площадь поверхности будет приближенно равна объему этого слоя, деленному на его толщину. Предельный переход при толщине, стремящейся к нулю дает точное значение площади. Однако, для площади по Минковскому не всегда выполняется свойство аддитивности. Обобщение данного определения приводит к понятию линии по Минковскому и другим[
Я что-то не договорил про площадь фигуры, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое площадь фигуры и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия
Комментарии
Оставить комментарий
Планометрия
Термины: Планометрия