Лекция
Привет, Вы узнаете о том , что такое равновеликие фигуры, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое равновеликие фигуры, равносоставленные фигуры , настоятельно рекомендую прочитать все из категории Планометрия.
.Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).
равновеликие фигуры — плоские фигуры, имеющие равные площади, или пространственные фигуры (тела), имеющие равные объемы. Всякие два простых (без самопересечений) равновеликих многоугольника являются и равносоставленными (теорема Бойаи — Гервина); два равновеликих многогранника, вообще говоря, не будут равносоставлены (теорема Дена — Кагана). Другими словами, равновеликие многоугольники можно перекроить, т. е. разрезать каждый из них на такие части, из которых можно составить другой многоугольник.
Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.
Равновеликие и равносоставленные фигуры . Равновеликие фигуры — плоские (пространственные) фигуры одинаковой площади (объема); равносоставленные фигуры — фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие равносоставленности применяется только к многоугольникам и многогранникам. Равносоставленные фигуры являются равновеликими. Венгерский математик Я. Больяй (1832) и немецкий математик П. Гервин (1833) доказали, что равновеликие многоугольники являются равносоставленными (теорема Больяй — Гервина). Поэтому разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат. Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику. Об этом говорит сайт https://intellect.icu . Эквивалентным понятию равносоставленности является понятие равнодополняемости, которое лежит в основе «метода дополнения», т. е. дополнения двух фигур равными частями так, чтобы получившиеся после такого дополнения фигуры были равны.
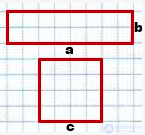
рисунок 1
1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.
Площадь прямоугольника
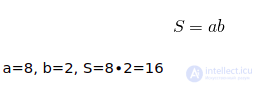
Площадь квадрата

То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если
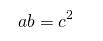
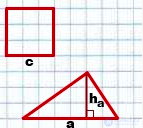
рисунок 2
2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.
Площадь квадрата S=3²=9.
Площадь треугольника
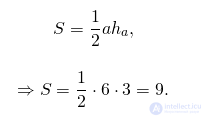
Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если
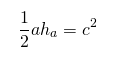
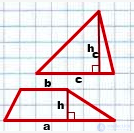
рисунок 3
3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.
Площадь треугольника
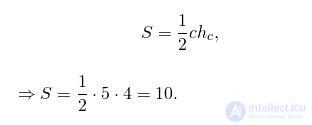
Площадь трапеции
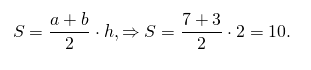
Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если
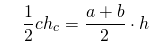
Исследование, описанное в статье про равновеликие фигуры, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое равновеликие фигуры, равносоставленные фигуры и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия
Из статьи мы узнали кратко, но содержательно про равновеликие фигуры
Комментарии
Оставить комментарий
Планометрия
Термины: Планометрия