Лекция
Привет, мой друг, тебе интересно узнать все про прямоугольник, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое прямоугольник, признак прямоугольника, золотой прямоугольник , настоятельно рекомендую прочитать все из категории Планометрия.
прямоугольник ом называется параллелограмм, у которого все углы прямые. Прямоугольник — четырехугольник, у которого все углы прямые (равны 90 градусам).
В евклидовой геометрии для того, чтобы четырехугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвертый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырехугольника не равна 360°, прямоугольников не существует.
Слово «прямоугольник» происходит от латинского rectangulus , которое представляет собой комбинацию лат. «rectus» (как прилагательное, правильный, правильный) и лат. «angulus» (угол)

Теорема.
Если у параллелограмма все углы равны, то он является прямоугольником.
Доказательство.
Пусть дан параллелограмм ABCD и ∠ A = ∠ B = ∠ С = ∠ D.
Углы A и B являются внутренними односторонними, а значит их сумма равна 180 º. По условию они равны, значит каждый из них равен 90 º. Значит, ∠ A = ∠ B = ∠ С = ∠ D = 90 º. А параллелограмм, у которого все углы прямые, есть прямоугольник. Теорема доказана.
Параллелограмм является прямоугольником, если выполняется любое из условий:
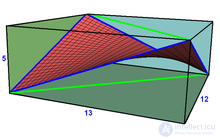
Седловидный прямоугольник имеет 4 непланарных вершины В этом примере показаны 4 синих края прямоугольника и две зеленые диагонали, каждая из которых является диагональю прямоугольных граней.
В сферической геометрии, сферической прямоугольник представляет собой фигуру, чьи четыре ребра большой окружности дуги, которые встречаются под равными углами больше 90 °. Об этом говорит сайт https://intellect.icu . Противоположные дуги равны по длине. Поверхность сферы в евклидовой твердотельной геометрии является неевклидовой поверхностью в смысле эллиптической геометрии. Сферическая геометрия - это простейшая форма эллиптической геометрии.
В эллиптической геометрии, эллиптическая прямоугольник представляет собой фигуру в эллиптической плоскости, четыре ребра эллиптические дуги , которые встречаются под равными углами больше 90 °. Противоположные дуги равны по длине.
В гиперболической геометрии, гиперболической прямоугольник представляет собой фигуру в гиперболической плоскости, четыре ребра гиперболические дуги , которые встречаются под равными углами менее 90 °. Противоположные дуги равны по длине
Прямоугольник используется во многих периодических моделях тесселяции , например, в кирпичной кладке :
 Сложенная облигация |
 Бегущая связь |
 Плетение корзины |
 Плетение корзины |
 Узор в елочку |
Прямоугольник, выложенный квадратами, прямоугольниками или треугольниками, называется «квадратным», «прямоугольным» или «треугольным» (или «треугольным») прямоугольником соответственно. Прямоугольник с мозаикой идеален , если плитки одинаковы и имеют конечное количество, и нет двух плиток одинакового размера. Если две такие плитки одинакового размера, плитка неидеальна . В идеальном (или несовершенном) треугольном прямоугольнике треугольники должны быть прямоугольными . . Наименьшее количество квадратов, необходимое для идеального замощения прямоугольника, - 9 [ а наименьшее число, необходимое для идеальной обработки квадрата, - 21, найденное в 1978 году с помощью компьютерного поиска.
Прямоугольник имеет соизмеримые стороны тогда и только тогда, когда он может быть выложен конечным числом неравных квадратов. То же самое верно, если плитки представляют собой неравные равнобедренные прямоугольные треугольники .
Наибольшее внимание привлекли мозаики прямоугольников другими плитками, которые представляют собой конгруэнтные непрямоугольные полимино , допускающие любые вращения и отражения. Есть также мозаики конгруэнтными полиаболами .
Пропорции золотого прямоугольника наблюдались еще в Вавилонской Скрижали Шамаша (ок. 888–855 до н.э.) хотя Марио Ливио называет любое знание золотого сечения до древних греков «сомнительным».
По словам Ливио, с момента публикации в 1509 году « пропорции божественности » Луки Пачоли «золотое сечение стало доступным для художников в теоретических трактатах, которые не были слишком математическими, которые они могли фактически использовать».
Вилла Штайн 1927 года, спроектированная Ле Корбюзье , в архитектуре некоторых зданий использовано золотое сечение , имеет размеры, близкие к золотым прямоугольникам.
В геометрии , А золотой прямоугольник представляет собой прямоугольник , на чьей стороне длина в золотой пропорции , , который
(греческая буква фи ), где
составляет приблизительно 1,618.
Золотые прямоугольники демонстрируют особую форму самоподобия : все прямоугольники, созданные путем добавления или удаления квадрата с конца, также являются золотыми прямоугольниками.
Я что-то не договорил про прямоугольник, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое прямоугольник, признак прямоугольника, золотой прямоугольник и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия
Из статьи мы узнали кратко, но содержательно про прямоугольник
Комментарии
Оставить комментарий
Планометрия
Термины: Планометрия