Лекция
Привет, Вы узнаете о том , что такое антипараллелограмм, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое антипараллелограмм , настоятельно рекомендую прочитать все из категории Планометрия.
В геометрии и планеметри антипараллелограмм является особым типом самопересекающегося четырехугольника . Подобно параллелограмму , антипараллелограмм имеет две противоположные пары сторон равной длины, но стороны более длинной пары пересекаются друг с другом, как в механизме ножниц . Антипараллелограммы также называют контрпараллелограммами или скрещенными параллелограммами
Антипараллелограмм - это частный случай скрещенного четырехугольника , у которого, как правило, неравные стороны Антипараллелограмм особой формы представляет собой скрещенный прямоугольник , в котором два противоположных края параллельны.
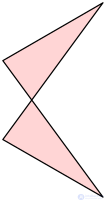
Антипараллелограмм, или контрпараллелограмм, — плоский четырехугольник, в котором каждые две противоположные стороны равны между собою, но не параллельны, в отличие от параллелограмма. Длинные противоположные стороны пересекаются между собою в точке, находящейся между их концами; пересекаются между собою и продолжения коротких сторон.
Если четырехугольник является антипараллелограммом, то его две пары противоположных сторон антипараллельны. Действительно, вершинами антипараллелограмма являются вершины равнобедренной трапеции, около которой всегда можно описать окружность (признак антипараллельности противоположных сторон). То есть боковые стороны равнобедренной трапеции антипараллельны, также антипараллельны диагонали равнобедренной трапеции
У каждого антипараллелограмма есть ось симметрии, проходящая через точку пересечения. Из-за этой симметрии он имеет две пары равных углов, а также две пары равных сторон. Вместе с воздушными змеями и равнобедренными трапециями антипараллелограммы образуют один из трех основных классов четырехугольников с осью симметрии. Выпуклая оболочка из антипараллелограмм является равнобедренной трапецией, и каждый антипараллелограмм может быть образован из непараллельных сторон и диагоналей равнобедренной трапеции. Как особый случай, антипараллелограмм также может быть образован из диагоналей и любой пары сторон прямоугольника .
Каждый антипараллелограмм представляет собой вписанный четырехугольник , что означает, что все его четыре вершины лежат на одной окружности .
Несколько невыпуклый равномерная многогранники , в том числе тетрагемигексаэдр , cubohemioctahedron , octahemioctahedron , небольшой rhombihexahedron , небольшой icosihemidodecahedron и небольшой dodecahemidodecahedron , имеют antiparallelograms как их фигуры вершин , поперечные сечения , образованные разрезанием многогранника плоскостью, проходящей рядом с вершиной, перпендикулярно ось между вершиной и центром.
Для однородных многогранников этого типа, у которых грани не проходят через центральную точку многогранника, двойственный многогранник имеет антипараллелограммы в качестве граней; примеры двойных однородных многогранников с гранями антипараллелограмма включают малый ромбигексакрон , большой ромбигексакрон , малый ромбидодекакрон , большой ромбидодекакрон , малый додецикосакрон и большой додецикосакрон . Антипараллелограммы, образующие грани этих двойственных однородных многогранников, являются теми же антипараллелограммами, которые образуют вершинную фигуру исходного однородного многогранника.
Одна из форм неоднородного, но изгибаемого многогранника , октаэдр Брикара , может быть построена как двойная пирамида над антипараллелограммом.
Антипараллелограмм использовался как форма четырехзвенной связи , в которой четыре жестких балки фиксированной длины (четыре стороны антипараллелограмма) могут вращаться относительно друг друга в соединениях, размещенных в четырех вершинах антипараллелограмма. В этом контексте его также называют связкой «бабочка» или « бабочка» . Как соединение, оно имеет точку нестабильности, в которой его можно преобразовать в параллелограмм и наоборот.
Если одно из коротких (непересеченных) ребер рычажного механизма антипараллелограмма зафиксировано на месте, а оставшееся звено движется свободно, то точка пересечения антипараллелограмма очерчивает эллипс , в фокусах которого находятся концы фиксированного ребра. Другой движущийся короткий край антипараллелограмма имеет в качестве своих концов фокусы другого движущегося эллипса, образованного от первого путем отражения по касательной линии через точку пересечения.
Как для параллелограммных, так и для антипараллелограммных рычажных механизмов, если один из длинных (скрещенных) краев рычажного механизма закреплен в качестве основания, свободные суставы перемещаются по равным кругам, но в параллелограмме они перемещаются в одном направлении с равными скоростями, находясь в Антипараллелограмм они движутся в противоположных направлениях с неодинаковыми скоростями. Как обнаружил Джеймс Ватт , если длинная сторона антипараллелограмма зафиксирована таким образом, он образует вариант соединения Ватта , а середина незафиксированного длинного края будет образовывать лемнискату или кривую в виде восьмерки. Для антипараллелограмма, образованного сторонами и диагоналями квадрата, это лемниската Бернулли .
Антипараллелограмм - важная особенность в конструкции инвертора Харта, рычажного механизма, который (как и рычаг Peaucellier – Lipkin ) может преобразовывать вращательное движение в прямолинейное. Соединение в форме антипараллелограмма также может использоваться для соединения двух осей четырехколесного транспортного средства, уменьшая радиус поворота транспортного средства по сравнению с подвеской, которая допускает поворот только одной оси. Пара вложенных антипараллелограммов использовалась в связи, определенной Альфредом Кемпе.как часть его теоремы об универсальности, утверждающей, что любая алгебраическая кривая может быть начерчена сочленениями соответственно определенной связи. Кемпе назвал связь вложенного антипараллелограмма «мультипликатором», поскольку ее можно было использовать для умножения угла на целое число.
Без распорок рычажок антипараллелограмма можно превратить в нормальный параллелограмм. Его можно использовать для предотвращения этого, используя конструкцию Эбботта и Бартона, 2004. Эта конструкция может быть использована для решения проблемы в теореме универсальности Кемпе .
В проблеме n тел , изучении движений точечных масс в соответствии с законом всемирного тяготения Ньютона , важную роль играют центральные конфигурации , решения проблемы n тел, в которых все тела вращаются вокруг некоторой центральной точки как если бы они были жестко связаны друг с другом. Например, для трех тел существует пять решений этого типа, заданных пятью лагранжевыми точками. Для четырех тел с двумя парами тел, имеющих равные массы (но с непрерывно изменяющимся соотношением масс двух пар), численные данные показывают, что существует непрерывное семейство центральных конфигураций, связанных друг с другом движением связь антипараллелограмм.
Исследование, описанное в статье про антипараллелограмм, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое антипараллелограмм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Планометрия
Из статьи мы узнали кратко, но содержательно про антипараллелограмм
Комментарии
Оставить комментарий
Планометрия
Термины: Планометрия